安徽省滁州市凤阳县2023-2024学年八年级上学期期中数学试卷
试卷更新日期：2024-03-08 类型：期中考试
一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A，B，C，D四个选项，其中只有一个是符合题目要求的。
-
1. 下列能够准确表示合肥市地理位置的是（ ）A、离北京市1017.9千米 B、在安徽省 C、在黄山的西北 D、东经117°，北纬32°2. 下面给出的四个三角形都有一部分被遮挡，其中不能判断三角形类型的是（ ）A、
B、
C、
D、
3. 经过点A（5，3），B（6，3）作直线AB ， 则直线AB（ ）A、经过点（5，0） B、平行于x轴 C、经过原点 D、平行于y轴4. 如图，BE是某个三角形的高，则这个三角形是（ ）
A、△ABE B、△ABD C、△CBE D、△ABC5. 将点A（0，0）先向左平移2023个单位长度，再向下平移5个单位长度后，得到的点B位于（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 下列命题是真命题的是（ ）A、（4，3）和（3，4）表示同一个点 B、垂线段最短 C、同位角相等 D、相等的角是对顶角7. 如图，小贤将一根长度为10cm的红色小棒分成两段，使它们可以和另一根绿色小棒首尾相接构成一个三角形．若绿色小棒长为a cm（a为正整数），则a的最大值为（ ）
A、10 B、9 C、8 D、78. 如图是小海为学校即将举办的“首届数学核心素养展示大赛”制作宣传海报时设计的艺术数字“1”，若BC⊥EF ， ∠ABC＝140°，∠AFE＝75°，则∠A的度数为（ ）
A、40° B、30° C、25° D、20°9. 如图1，∠B＝∠C＝90°，AB＝2CD ， 点P以每秒1cm的速度从点B出发，沿B﹣C﹣D路线运动，到点D停止．图2反映的是△ABP的面积S（cm2）与点P的运动时间x（秒）两个变量之间的关系．则m的值为（ ）
A、20 B、24 C、10 D、1210. 如图，一次函数y＝kx+b（k ， b是常数，且k≠0）的图象与正比例函数y＝mx（m是常数，且m≠0）的图象相交于点M（﹣2，1），下列判断不正确的是（ ）
A、关于x的方程mx＝kx+b的解是x＝﹣2 B、关于x ， y的方程的解是 C、当x＞﹣2时，函数y＝kx+b的值比函数y＝mx的值大 D、关于x的不等式（m﹣k）x＞b的解集是x＞﹣2二、填空题（本大题共4小题，每小题5分，满分20分
-
11. 已知一个三角形三个内角度数的比是1：3：6，则其最小内角的度数为 ．12. 如图，以BE为边的三角形有 个．
13. 已知点 在x轴上，则m等于.14. 如图，在平面直角坐标系中，点A（0，2），点B（3，0），点C在第四象限，线段BC∥y轴，且BC＝4，在第二象限有点P ．
(1)、点C的坐标为 ；(2)、当四边形ABOP的面积与三角形ABC的面积相等时，m的值为 ．三、（本大题共2小题，每小题8分，满分16分）
-
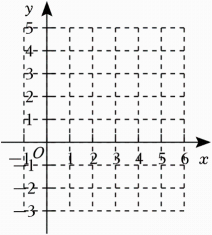
15. 请在如图所示的平面直角坐标系中描出下列各点．
A（5，﹣2），B（3，0），C（2，1），D（6，3）．
16. 如图，在△ABC中，∠B＝40°，∠C＝60°，AD平分∠BAC ， DE⊥BC交AB于点E ．求∠ADE的度数．
四、（本大题共2小题，每小题8分，满分16分）
-
17. 如图，△ABC的高AD＝6cm ， BC＝9cm ， 点E在BD上，连接AE ． 设CE的长为x（cm），△ABE的面积为y（cm2），解答下列问题：
(1)、求y与x之间的关系式；(2)、若CD＝4cm ， 当x为多少时，△ABE的面积比△ADE的面积大3cm2 ．18. 已知函数y= x+3．(1)、请在所给的平面直角坐标系中画出该函数的图象．
(2)、结合所画图象，分别求出在函数图象上满足下列条件的点的坐标．①横坐标是﹣4；
②和x轴的距离是2个单位长度．
五、（本大题共2小题，每小题10分，满分20分）
-
19. 如图，这是一个被抹去了平面直角坐标系的网格图，网格中每个小正方形的边长均为1个单位长度，△ABC的各顶点都在网格的格点上，若记点A的坐标为（﹣1，3），点C的坐标为（1，﹣1）．
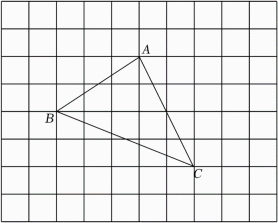(1)、请在图中建立平面直角坐标系．(2)、写出点B的坐标．(3)、将△ABC先向下平移2个单位长度，再向右平移3个单位长度得到△A'B'C'，请画出△A'B'C'．20. 如图所示，根据图中信息．
(1)、m＝ ▲ ；n＝ ▲ ；点P的坐标为 ▲ ；(2)、当x为何值时，y1＞y2；(3)、求 S△APB ．六、（本题满分12分）
-
21. 如图，直线l1与x轴交于点A ， 与y轴交于点B（0，﹣2），且与直线y=x平行．
(1)、求直线l1的解析式；(2)、在x轴上，点A左侧有一点C ，①若线段AC＝3，则点C的坐标是 ▲ ；
②若直线l2：y＝kx+b过点（0，6），且与x轴的交点在线段AC上（包括端点），求k的取值范围．
七、（本题满分12分）
-
22. “五一”劳动节到了，为在学生中弘扬劳动精神，让学生在做中学、学中做、家校合力共推劳动教育．五一假期老师布置了与父母互换身份，做一天父母的工作，体会劳动并感受父母的艰辛，理解、感恩父母，小李和妈妈互换身份，帮妈妈卖干果，他上午卖出4kg甲种类和3kg乙种类干果获得利润为85元，下午卖出7kg甲种类和5kg乙种类干果获得利润为145元．(1)、求每千克甲种类干果和乙种类干果的销售利润各是多少；(2)、小李的妈妈想一次购进两种干果共100kg用于销售，其中乙种类干果的进货量不超过甲种类干果的进货量的 ， 请你帮小李妈妈设计一种进货方案使销售总利润最大，并求出总利润的最大值．
八、（本题满分14分）
-
23. 将一把直角尺放置在钝角△ABC（∠BAC＞90°）上，使得点B、C分别在该直角尺的两条直角边DE、DF上，且直角顶点D与点A在BC边的同侧．
(1)、如图，点A在直角尺内部．①若∠A＝120°，∠ABD＝10°，求∠ACD的度数；
②若∠A＝α，∠ABD＝β，求∠ACD的度数（用含α、β的式子表示）．
(2)、改变直角尺的位置，使点A在直角尺外部，其它条件不变，探索∠ABD、∠ACD、∠A三者之间的数量关系，并说明理由．
-
-