重庆市渝北区六校联盟2023-2024学年七年级上学期第二次大练兵(期中)数学试题
试卷更新日期:2024-03-08 类型:期中考试
一、选择题(本大题共10小题,每题4分,共40分),每小题下都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填在答题卡对应的横线上。
-
1. 在 , , , 这四个数中,最大的数是( )A、 B、 C、 D、2. 下面计算正确的是( )A、3x2-x2=3 B、3a2+2a3=5a5 C、-0.25ab+ ab=0 D、x+3=3x3. 在数 , , , , , , 中,有理数有( )A、个 B、个 C、5个 D、6个4. 下列说法正确的是( )A、系数是 , 次数是 B、是负数 C、和的结果相等 D、多项式是二次三项式5. 下列各式中与的值不相等的是( )A、 B、 C、 D、6. 已知关于的多项式不含三次项和一次项,则的值为( )A、 B、 C、 D、7. 已知 , , 且 , 则的值为( )A、 B、 C、或 D、或8. 若甲班有人,乙班有人,现从乙班调往甲班一些人,使甲班人数是乙班人数的倍,设从乙班调往甲班人,根据题意,可列方程( )A、 B、 C、 D、9. 如图,每一个图形都是由一些小黑方块按一定的规律排列组成的,其中第个图形中有个小黑方块,第个图形中有个小黑方块,第个图形中有个小黑方块 , 按此规律,则第个图中小黑方块的个数是( )
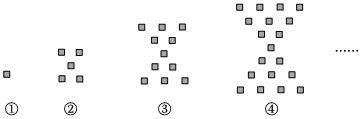 A、 B、 C、 D、10. 已知两个多项式 , , 以下结论中正确的个数有( )
A、 B、 C、 D、10. 已知两个多项式 , , 以下结论中正确的个数有( )若 , 则;若的值与的值无关,则;若 , 则;若关于的方程的解为整数,则符合条件的非负整数有个.
A、个 B、个 C、个 D、个二、填空题(本大题共8小题,每题4分,共32分)
-
11. 2023年10月26日,神州十七号载人飞船发射成功,成功对接空间站.据悉,在超过200摄氏度的大温差、长期低温、强辐射的空间环境中,飞船舱内环境温度会始终控制在22℃±4℃,为航天员营造舒适的温度环境.可知,载人飞船座舱内的最高温度是℃.12. 据统计,2023年1-10月,重庆新能源汽车的产量约为506000辆,占重庆市汽车产量比重为14.5%.将数506000用科学记数法表示为 .13. 单项式的系数是 , 次数是 .14. 若与是同类项,则 .15. 若关于的方程是一元一次方程,则的值是 .16. 若 , 都是有理数,定义一种新运算“”,规定一种运算:ab= , 如(﹣3)(2)= , 则5(﹣)的值为 .17. 如图是年月份的日历表,用形如
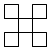 的框架框住日历表中的五个数,对于框架框住的五个数字之和,小明的计算结果有 , , , , 小华说有结果是错误的.通过计算,可知小明的计算结果中错误的是 .
的框架框住日历表中的五个数,对于框架框住的五个数字之和,小明的计算结果有 , , , , 小华说有结果是错误的.通过计算,可知小明的计算结果中错误的是 . 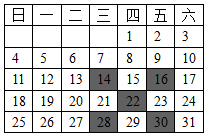 18. 如果有个不同的正整数、、、满足 , 那么的最大值为 .
18. 如果有个不同的正整数、、、满足 , 那么的最大值为 .三、解答题:(本大题共8个小题,19题8分,20-26每题10分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答过程书写在答题卡中对应的位置上.
-
19. 把下列各数分别填入相应的集合里.
, , , , , , , , л.
(1)、正数集合:;(2)、负数集合:_;(3)、整数集合:;(4)、分数集合: .20. 计算:(1)、;(2)、 .21. 解方程:(1)、(2)、 .22. 先化简,再求值: , 其中 .23. 有理数、、在数轴上的位置如图所示: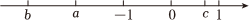 (1)、较、、的大小用“”连接;(2)、化简丨丨丨丨丨丨.24. 某商场用元购进 , 两种新型节能台灯共盏,这两种台灯的进价、标价如下表所示.
(1)、较、、的大小用“”连接;(2)、化简丨丨丨丨丨丨.24. 某商场用元购进 , 两种新型节能台灯共盏,这两种台灯的进价、标价如下表所示.类型
型
型
进价元盏
标价元盏
(1)、这两种台灯各购进多少盏?(2)、若型台灯按标价的折出售,型台灯按标价的折出售,那么这批台灯全部售出后,商场共获利多少元?25. 定义:对任意一个两位数 , 如果满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“互异数”将一个“互异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与的商记为例如: , 对调个位数字与十位数字得到新两位数 , 新两位数与原两位数的和为 , 和与的商为 , 所以 .根据以上定义,回答下列问题:
(1)、下列两位数 , , 中,“互异数”为;;(2)、若“互异数”满足 , 求所有“互异数” .26. 如图,在数轴上点表示数 , 点示数 , 、满足;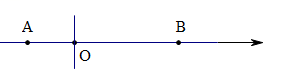 (1)、点表示的数为;点表示的数为;(2)、若点与点之间的距离表示为 , 点与点之间的距离表示为 , 请在数轴上找一点 , 使 , 则点表示的数;(3)、若在原点处放一挡板,一小球甲从点处以个单位秒的速度向左运动;同时另一小球乙从点处以个单位秒的速度也向左运动,在碰到挡板后忽略球的大小,可看作一点以原来的速度向相反的方向运动,设运动的时间为秒 , 当甲、乙相距个单位长度时,求的值.
(1)、点表示的数为;点表示的数为;(2)、若点与点之间的距离表示为 , 点与点之间的距离表示为 , 请在数轴上找一点 , 使 , 则点表示的数;(3)、若在原点处放一挡板,一小球甲从点处以个单位秒的速度向左运动;同时另一小球乙从点处以个单位秒的速度也向左运动,在碰到挡板后忽略球的大小,可看作一点以原来的速度向相反的方向运动,设运动的时间为秒 , 当甲、乙相距个单位长度时,求的值.