山西省大同市平城区两校联考2023-2024学年八年级上学期月考数学试题

试卷更新日期：2024-03-08 类型：月考试卷

进入出卷网下载

一、选择题（3×8＝24分）

1. 下列运算正确的是（）

A、x³+x³=2x⁶ B、x⁸÷x²=x⁴ C、x^m•xⁿ=x^mn D、（﹣x⁵）⁴=x²⁰

查看试题解析
2. 下列等式从左到右的变形是因式分解的是（）

A、 $12 a^{2} b = 3 a \cdot 4 a b$ B、 $(x + 3) (x - 3) = x^{2} - 9$ C、 $4 x^{2} + 8 x - 1 = 4 x (x + 2) - 1$ D、 $\frac{1}{2} a x - \frac{1}{2} a y = \frac{1}{2} a (x - y)$

查看试题解析
3. 若 $| a | = 2$ ，且 $(a - 2)^{0} = 1$ ，则 $a$ 的值为（）

A、2 B、 $- 2$ C、 $\pm 2$ D、除 $- 2$ 以外的任何值

查看试题解析
4. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，再将剩下的阴影部分剪开，拼成下边的长方形．根据图形的变化过程可以验证下列哪一个等式成立（）．

A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 $a (a + b) = a^{2} + a b$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a - b) (a + b) = a^{2} - b^{2}$

查看试题解析
5. 如果（x+a）（x+b）的结果中不含x的一次项，那么a、b满足（　　）

A、a=b B、a=0 C、a=﹣b D、b=0

查看试题解析
6. 计算 ${(- 0.25)}^{2023} \times {(- 4)}^{2024}$ 的结果是（）

A、 $- \frac{1}{4}$ B、 $\frac{1}{4}$ C、 $- 4$ D、4

查看试题解析
7. 已知， $a = 2^{55}$ ， $b = 3^{44}$ ， $c = 4^{33}$ ，则a、b、c的大小关系是（）

A、 $b > c > a$ B、 $a > b > c$ C、 $c > a > b$ D、 $c > b > a$

查看试题解析
8. 如果把分式 $\frac{10 x}{x + y}$ 中的x ， y都扩大10倍，则分式的值（）

A、扩大100倍 B、扩大10倍 C、不变 D、缩小为原来的 $\frac{1}{10}$

查看试题解析

二、填空题（3×5＝15分）

9. 约分： $\frac{x^{2} - 4}{x^{2} - 2 x} =$ ．

查看试题解析
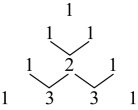
10. 如果多项式 $y^{2} - 2 m y + 1$ 是完全平方式，那么 $m =$ ．

查看试题解析
11. 若 $a + b = 15$ ， $a^{2} + b^{2} = 125$ ，则 $a b =$ ．

查看试题解析
12. 当x＝时，分式 $\frac{| x | - 1}{x - 1}$ 的值为零．

查看试题解析
13. 如图为杨辉三角系数表，它的作用是指导读者按规律写出形如 $(a + b)^{n}$ （其中 $n$ 为正整数）展开式的系数，例如： $(a + b) = a + b$ ， $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ， ${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ ，那么 $(a + b)^{4}$ 展开式中系数分别为．

查看试题解析

三、解答题

14. 计算

(1)、 ${(- a^{2})}^{3} - {(- 3 a^{3})}^{2} - a \cdot (- a)^{5}$ ；

(2)、 $(25 x^{2} + 15 x^{3} y - 20 x^{4}) \div {(- 5 x)}^{2}$ ；

(3)、 $3 {(x + 1)}^{2} - 2 (x + 1) (x - 1)$ ．

查看试题解析
15. 因式分解

(1)、 $x^{3} - 4 x$ ；

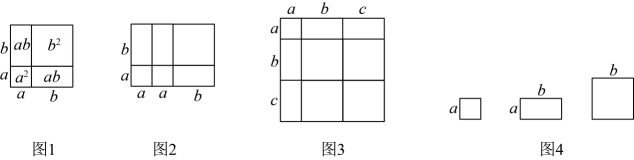
(2)、 $3 x^{2} y - 12 x y + 12 y$ ；

(3)、 ${(x^{2} + 4)}^{2} - 16 x^{2}$ ．

查看试题解析
16. 先化简，再求值： $a (a - 2 b) + {(a + b)}^{2}$ ，其中 $a = - 1$ ， $b = \sqrt{2}$ ．

查看试题解析
17. 已知a、b、c是 $△ A B C$ 三边长，且 $a^{2} - 8 a + b^{2} - 6 b + c^{2} - 6 c + 34 = 0$ ，试判断 $△ A B C$ 的形状．

查看试题解析
18. 已知 $A$ 是一个多项式，单项式 $B$ 等于 $3 x$ ，某同学计算 $A \div B$ 时，把 $A \div B$ 误写成 $A + B$ ，结果得出 $x^{3} - 4 x^{2} + 6 x$ ，求 $A \div B$ ．

查看试题解析
19. 【阅读材料】“数形结合”是一种非常重要的数学思想方法．比如：在学习“整式的乘法”时，我们通过构造几何图形，用“等积法”直观地推导出了完全平方和公式： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ （如图1）．利用“数形结合”的思想方法，可以从代数角度解决图形问题，也可以用图形关系解决代数问题．
【方法应用】根据以上材料提供的方法，完成下列问题：

(1)、由图2可得等式：；由图3可得等式：；

(2)、利用图3得到的结论，解决问题：若 $a + b + c = 15$ ， $a b + a c + b c = 35$ ，则 $a^{2} + b^{2} + c^{2} =$ ；

(3)、如图4，若用其中 $x$ 张边长为 $a$ 的正方形， $y$ 张边长为 $b$ 的正方形， $z$ 张边长分别为a、b的长方形纸片拼出一个面积为 $(2 a + b) (a + 2 b)$ 长方形（无空隙、无重叠地拼接），则 $x + y + z =$ ．

查看试题解析
20. 读下面的材料
并解答后面的问题：
小李：能求出 $x^{2} + 4 x - 3$ 的最小值吗？如果能，其最小值是多少？
小华：能．求解过程如下：
因为 $x^{2} + 4 x - 3$
$= x^{2} + 4 x + 4 - 4 - 3$
$= (x^{2} + 4 x + 4) - (4 + 3)$
$= (x + 2)^{2} - 7$
而 $(x + 2)^{2} \geq 0$ ，所以 $x^{2} + 4 x - 3$ 的最小值是 $- 7$ ．
问题：

(1)、你能否求出 $x^{2} - 6 x + 4$ 的最小值？如果能，写出你的求解过程．

(2)、你能否求出 $6 - x^{2} + 2 x$ 的最大值？如果能，写出你的求解过程．

查看试题解析