湖南省娄底市涟源市2023-2024学年高一上学期1月期末考试数学试题

试卷更新日期：2024-03-08 类型：期末考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知集合 $A = {- 1 ， 0 ， 1 ， 2} ， B = {0 ， 1 ， 2 ， 3}$ ，则 $A ∩ B =$ （）

A、 ${0 ， 1 ， 2}$ B、 ${1 ， 2 ， 3}$ C、 ${- 1 ， 3}$ D、 ${- 1 ， 0 ， 1 ， 2 ， 3}$

查看试题解析
2. 若 $c o s α = \frac{12}{13}$ ，且 $α$ 为第一象限角，则 $t a n α$ 的值为（）

A、 $\frac{12}{5}$ B、 $- \frac{12}{5}$ C、 $\frac{5}{12}$ D、 $- \frac{5}{12}$

查看试题解析
3. 函数 $f (x) = 2^{x} + 2 x - 7$ 的零点所在的区间为（）

A、 $(1 ， 2)$ B、 $(2 ， 3)$ C、 $(3 ， 4)$ D、 $(4 ， 5)$

查看试题解析
4. 若 $x > 0$ ，则 $x + \frac{1}{x}$ 的最小值为

A、2 B、4 C、6 D、8

查看试题解析
5. 已知命题 $p ： \forall x \in (0 ， + \infty)$ ， $x^{3} > x$ ，则命题 $p$ 的否定是（）

A、 $\forall x \in (0 ， + \infty)$ ， $x^{3} \leq x$ B、 $\exists x \in (0 ， + \infty)$ ， $x^{3} \leq x$ C、 $\exists x \in (0 ， + \infty)$ ， $x^{3} < x$ D、 $\forall x \notin (0 ， + \infty)$ ， $x^{3} > x$

查看试题解析
6. 下列函数中，是奇函数且在区间 $(0 ， + ∞)$ 上单调递增的是（）

A、 $f (x) = x^{\frac{1}{2}}$ B、 $f (x) = x^{2}$ C、 $f (x) = \frac{1}{x}$ D、 $f (x) = x^{3}$

查看试题解析
7. 已知 $a = 4^{0.1} ， b = 2^{0.6} ， c = l o g_{4} 0.6$ ，则 $a ， b ， c$ 的大小关系为（）

A、 $c < a < b$ B、 $c < b < a$ C、 $a < b < c$ D、 $b < a < c$

查看试题解析
8. 甲、乙分别解关于x的不等式 $x^{2} + b x + c < 0$ ．甲抄错了常数b，得到解集为 $(- 6 ， 1)$ ；乙抄错了常数c，得到解集为 $(2 ， 3)$ ．如果甲、乙两人解不等式的过程都是正确的，那么原不等式解集应为（）

A、 $(- 1 ， 6)$ B、 $(1 ， 6)$ C、 $(- 2 ， 3)$ D、 $(- 3 ， - 2)$

查看试题解析

二、多项选择题：本题共4小题，毎小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 已知实数 $a ， b ， c$ ，其中 $a > b > 1$ ，则下列关系中恒成立的是（）

A、ab＞b² B、ac²＜bc² C、a-c＞b-c D、 $a + \frac{1}{b} ＞ b + \frac{1}{a}$

查看试题解析
10. 下列说法正确的是（）

A、函数 $y = a^{x + 2} - 2$ $(a > 0 ， a \neq 1)$ 的图像恒过定点 $A (- 2 ， - 1)$ B、 $“ 0 ＜ x ＜ 5 ”$ 是 $“ - 1 ＜ x ＜ 5 ”$ 的充分不必要条件 C、函数 $y = t a n x$ 的最小正周期为 $π$ D、函数 $y = \sqrt{x^{2} + 5} + \frac{1}{\sqrt{x^{2} + 5}}$ 的最小值为 $2$

查看试题解析
11. 若 $α \in (0 ， π)$ ， $s i n α - c o s α = \frac{1}{5}$ ，则（）

A、 $t a n α = \frac{4}{3}$ B、 $s i n 2 α = \frac{12}{25}$ C、 $s i n α + c o s α = \frac{7}{5}$ D、 $c o s 2 α = - \frac{7}{25}$

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} (a - 2) x + 1 ， x \leq 0 ， \\ x^{a} ， x > 0 ， \end{array}$ 则以下说法正确的是（）

A、若 $a = - 1$ ，则 $f (x)$ 是 $(0 ， + \infty)$ 上的减函数 B、若 $a = 0$ ，则 $f (x)$ 有最小值 C、若 $a = \frac{1}{2}$ ，则 $f (x)$ 的值域为 $(0 ， + \infty)$ D、若 $a = 3$ ，则存在 $x_{0} \in (1 ， + \infty)$ ，使得 $f (x_{0}) = f (2 - x_{0})$

查看试题解析

三、填空题：本大题共4小题，每小题5分，共20分.

13. $2^{\log_{2} 3} + \log_{3} 1$ =.

查看试题解析
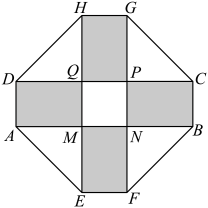
14. 已知 $f (x + 1) = 2 x - 3$ ，则 $f (4) =$ .

查看试题解析
15. 已知扇形的圆心角为 $\frac{π}{4}$ ，弧长为 $\frac{2 π}{3}$ ，则该扇形的面积为.

查看试题解析
16. 某公园设计了一座八边形的绿化花园，它的主体造型平面图（如图2）是由两个相同的矩形ABCD和EFGH构成的面积为 $80 m^{2}$ 的十字型区域，计划在正方形MNPQ上建一座花坛，造价为99元/ $m^{2}$ ；在四个空角（图中四个三角形）上铺草坪，造价为8元/ $m^{2}$ ；在四个矩形（图中阴影部分）上不做任何设计．设总造价为S（单位：元），AD长为x（单位：m），则绿化花园总造价S的最小值为元．

查看试题解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. 计算：

(1)、 $\sqrt{(- 4)^{2}} + (π - 1)^{0} - (\sqrt[3]{3})^{6} - l n \sqrt{e}$ ；

(2)、求函数f（x）＝ $\sqrt{2^{x} - 1}$ ＋ $\frac{1}{x - 2}$ 的定义域。

查看试题解析
18. 已知 $f (α) = \frac{s i n (π + α)}{t a n (π - α)}$ ．

(1)、求 $f (\frac{5 π}{6})$ 的值；

(2)、已知 $f (\frac{π}{3} - α) = \frac{2}{3}$ ，求 $s i n (α + \frac{π}{6})$ 的值．

查看试题解析
19. 已知函数 $f (x) = l o g_{a} (x + 1) - l o g_{a} (1 - x)$ ，其中 $a > 0$ 且 $a \neq 1$ .

(1)、判断 $f (x)$ 的奇偶性；

(2)、若 $a > 1$ ，解关于x的不等式 $f (x) > 0$ .

查看试题解析
20. 已知函数 $f (x) = 2 \sqrt{3} \cos^{2} \frac{x}{2} - 2 \sin (\frac{x}{2} + \frac{π}{2}) \cos (\frac{x}{2} + \frac{π}{2}) - \sqrt{3}$ .

(1)、求 $f (x)$ 的最小正周期；

(2)、求 $f (x)$ 在区间 $[0 ， π]$ 上的最小值及单调减区间.

查看试题解析
21. 某企业采用新工艺，把企业生产中排放的二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为100吨，最多为600吨，月处理成本 $f (x)$ （元）与月处理量x（吨）之间的函数关系可近似地表示为 $f (x) = \frac{1}{2} x^{2} - 200 x + 80000$ ．

(1)、该单位每月处理量为多少吨时，才能使月处理成本最低？月处理成本最低多少元？

(2)、该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？每吨的平均处理成本最低是多少元？

查看试题解析
22. 已知函数 $f (x)$ 是定义在 $R$ 上的奇函数，当 $x \geq 0$ 时， $f (x) = 1 - a \cdot 2^{x}$ ．

(1)、求 $a$ 的值；

(2)、求 $f (x)$ 在 $R$ 上的解析式；

(3)、若函数 $g (x) = f (x) - k \cdot 2^{x}$ 有零点，求实数 $k$ 的取值范围．

查看试题解析