湖南省邵阳市2023-2024学年高一上学期1月联考(期末)数学试题
试卷更新日期:2024-03-08 类型:期末考试
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的
-
1. 设集合 , 则( )A、 B、 C、 D、2. 已知命题 , 则命题的否定为( )A、 B、 C、 D、3. 已知 , 则的值为( )A、 B、 C、3 D、-34. 已知 , 则( )A、 B、 C、 D、5. 函数的定义域为( )A、 B、 C、 D、6. 若正实数满足 , 则的最大值为( )A、 B、 C、 D、7. 已知函数 , 若存在满足 , 且 , 则的最小值为( )A、5 B、6 C、7 D、88. 已知函数.若 , 则实数的取值范围是( )A、 B、 C、 D、
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 已知均为实数,且 , 则下列结论正确的有( )A、 B、 C、 D、10. 已知函数的部分图象如图所示,则下列说法正确的有( )
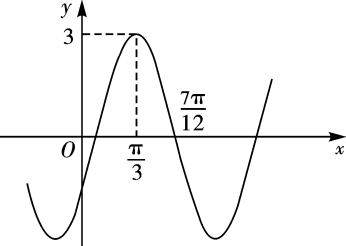 A、为偶函数 B、的图象向左平移个单位长度后得到的图象 C、图象的对称中心心 D、在区间上的最小值为11. 下列命题为真命题的有( )A、函数的单调递减区间为 B、函数的图象关于点对称 C、函数与函数是同一个函数 D、函数的最小值为-112. 已知函数在上单调递增,则实数的可能取值为( )A、-3 B、-2 C、0 D、3
A、为偶函数 B、的图象向左平移个单位长度后得到的图象 C、图象的对称中心心 D、在区间上的最小值为11. 下列命题为真命题的有( )A、函数的单调递减区间为 B、函数的图象关于点对称 C、函数与函数是同一个函数 D、函数的最小值为-112. 已知函数在上单调递增,则实数的可能取值为( )A、-3 B、-2 C、0 D、3三、填空题:本题共4小题,每小题5分,共20分.
-
13. 已知扇形的圆心角是2,半径为2,则扇形的面积为.14. 函数且是常数的图象过定点.15. 若 , 则.16. 创新是一个国家、一个民族发展进步的不竭动力,是推动人类社会进步的重要力量.某学校为了培养学生科技创新能力,成立科技创新兴趣小组,该小组对一个农场内某种生物在不受任何条件的限制下其数量增长情况进行研究,发现其数量(千只)与监测时间(单位:月)的关系与函数模型且)基本吻合.已知该生物初始总量为3千只,2个月后监测发现该生物总量为6千只.若该生物的总量再翻一番,则还需要经过个月.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 已知集合.(1)、若 , 求实数的取值范围;(2)、若“”是“”的充分条件,求实数的取值范围.18. 化简求值:(1)、;(2)、.19. 定义在上的奇函数 , 已知当时,.(1)、求在上的解析式;(2)、若时,不等式恒成立,求实数的取值范围.20. 已知函数.(1)、先把函数的图象向右平移个单位;再把曲线上各点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象,求函数的单调递增区间;(2)、若函数在上的最大值为3,求的值.