广西南宁市2023-2024学年高二上学期1月教学质量调研(期末)数学试题
试卷更新日期:2024-03-08 类型:期末考试
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
-
1. 若直线过点 , , 则该直线的斜率是( )A、 B、 C、 D、2. 已知数列是等差数列,为其前项和, , , 则的值为( )A、48 B、56 C、81 D、1003. 已知方程表示双曲线,则的取值范围是( )A、 B、 C、 D、或4. 已知数列满足 , , 则 ( )A、 B、2 C、12 D、335. 如图,在四面体OABC中, , , .点M在OA上,且 , 为BC中点,则等于( )
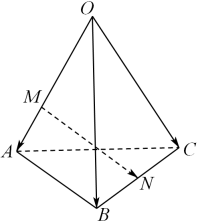 A、 B、 C、 D、6. 在正项等比数列中,为其前n项和,若 , 则的值为( )A、10 B、18 C、36 D、407. 已知点和圆:一束光线从点经轴反射到圆上的最短路程是( )A、 B、8 C、 D、108. 已知椭圆的左右焦点分别为 , 点在上,四边形是等腰梯形, , 则的离心率的取值范围是( )A、 B、 C、 D、
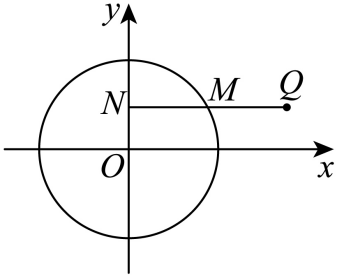
A、 B、 C、 D、6. 在正项等比数列中,为其前n项和,若 , 则的值为( )A、10 B、18 C、36 D、407. 已知点和圆:一束光线从点经轴反射到圆上的最短路程是( )A、 B、8 C、 D、108. 已知椭圆的左右焦点分别为 , 点在上,四边形是等腰梯形, , 则的离心率的取值范围是( )A、 B、 C、 D、二、 选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
-
9. 在正方体中,能作为空间的一个基底的一组向量有( )A、 , , B、 , , C、 , , D、 , ,10. 下列说法错误的有( )A、若 , 则直线的斜率大于0 B、过点且斜率为的直线的点斜式方程为 C、斜率为 , 在y轴上的截距为3的直线方程为 D、经过点且在x轴和y轴上截距(截距均不为0)相等的直线方程为11. 已知数列 , 为其前项和,下列说法正确的是( )A、若 ,则是等差数列 B、若 ,则是等比数列 C、若是等差数列,则 D、若是等比数列,且 则12. 已知正方体的棱长为1,为棱(包含端点)上的动点,下列命题正确的是( )A、二面角的大小为 B、 C、若在正方形内部,且 , 则点的轨迹长度为 D、若平面 , 则直线与平面所成角的正弦值的取值范围为
三、填空题:本题共4小题,每小题5分,共20分.
-
13. 已知圆的方程为 , 则圆的半径为 .14. 已知 , , , 则在上的投影向量的模为 .15. 已知函数且过定点 , 直线过定点 , 则 .16. 记数列的前项和为 , 若 , 且是等比数列的前三项,则 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 已知等轴双曲线的对称轴都在坐标轴上,并且经过点 , 求双曲线的标准方程、离心率、实轴长18. 已知等比数列的各项均为正数,且 , .(1)、求的通项公式;(2)、数列满足 , 求的前项和 .19. 已知圆 .(1)、已知直线l: , 求该直线截得圆C的弦AB的长度;(2)、若直线过点且与圆C相交于M , N两点,求的面积的最大值,并求此时直线的方程.20. 如图,在直角梯形中,∥ , , . 以直线为轴,将直角梯形旋转得到直角梯形 , 且 .
 (1)、求证:∥平面;(2)、在线段上是否存在点 , 使得直线和平面所成角的正弦值为?若存在,求出的值;若不存在,说明理由.
(1)、求证:∥平面;(2)、在线段上是否存在点 , 使得直线和平面所成角的正弦值为?若存在,求出的值;若不存在,说明理由.