广西南宁市2023-2024学年高一上学期1月教学质量调研(期末)数学试题
试卷更新日期:2024-03-08 类型:期末考试
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
-
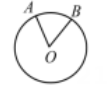
1. 已知集合 , , 则( )A、 B、 C、 D、2. 已知是实数,“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 已知命题“ , 使得”是真命题,则实数的取值范围为( )A、 B、 C、 D、4. 如图,在半径的圆形金属板上截取一块扇形板 , 使其面积为 , 则圆心角为( )
 A、 B、 C、 D、5. 在平面直角坐标系中,已知角的顶点与坐标原点重合,始边与轴的非负半轴重合,终边经过点 , 下列结论错误的是( )A、 B、 C、 D、6. 已知函数为奇函数,函数为偶函数, , 则( )A、 B、 C、 D、7. 在同一平面直角坐标系中,指数函数 , 二次函数的图象可能是( )A、
A、 B、 C、 D、5. 在平面直角坐标系中,已知角的顶点与坐标原点重合,始边与轴的非负半轴重合,终边经过点 , 下列结论错误的是( )A、 B、 C、 D、6. 已知函数为奇函数,函数为偶函数, , 则( )A、 B、 C、 D、7. 在同一平面直角坐标系中,指数函数 , 二次函数的图象可能是( )A、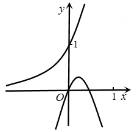 B、
B、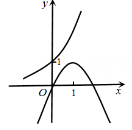 C、
C、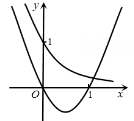 D、
D、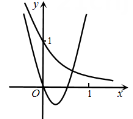 8. 已知函数有个零点,则实数的取值范围是( )A、 B、 C、 D、
8. 已知函数有个零点,则实数的取值范围是( )A、 B、 C、 D、二、 选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得.
-
9. 已知 , 则下列不等式中正确的是( )A、 B、 C、 D、10. 已知函数 , 则下列结论正确的是( )A、函数的定义域为 B、函数的值域为 C、函数的图象关于轴对称 D、函数在上单调递增11. 关于函数的零点,下列说法正确的是( )A、函数的零点个数为 B、函数的零点是 C、函数在内不存在零点 D、用二分法求函数在内的零点的近似值可取为(结果精确到)12. 已知函数关于的方程有个不同的实数根,则下列选项正确的是( )
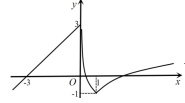 A、函数的零点个数为 B、实数的取值范围为 C、函数无最值 D、函数在上单调递增
A、函数的零点个数为 B、实数的取值范围为 C、函数无最值 D、函数在上单调递增三、填空题:本题共4小题,每小题5分,共20分.
-
13. 已知幂函数的图象过点 , 则.14. 已知 , 则函数的最小值为.15. 已知函数的部分图象如图所示,则的解析式为.
 16. 已知 , 且满足 , 则实数的取值范围为.
16. 已知 , 且满足 , 则实数的取值范围为.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 计算:(1)、 (其中);(2)、 .18. 已知 .(1)、 化简;(2)、 若 , 且 , 求的值.19. 已知函数.(1)、 求函数的定义域, 写出函数的单调区间(不必说明理由);(2)、 当时,函数的值域为 , 求实数的取值范围.20. 某运输公司今年初用万元购进一台大型运输车用于运输.若该公司预计从第年到第年花在该台运输车上的维护费用总计为万元,该车每年运输收入为万元.(1)、 该运输车从第几年开始盈利(即总收入减去成本及所有维护费之差为正值)?(2)、 若该车运输若干年后,有以下两种处理方案,哪一种方案效益更高?请说明理由.
方案一:当年平均盈利达到最大值时,以万元的价格卖出该运输车;
方案二:当盈利总额达到最大值时,以万元的价格卖出该运输车.
21. 超速行驶是引发交通事故的主要原因之一,交管部门提醒广大驾驶人合理控制车速,提高安全意识。某公路局经多次实验得到一辆汽车的行车速度(单位:)()与停车距离(单位:)的下列数据:为了描述速度与停车距离的关系,现有以下三种模型供选择:
① , ② , ③.
(1)、 根据上表的数据信息,选出你认为最符合实际的函数模型(不必说明理由),并利用表中两组数据和 , 求出相应的解析式;(2)、 一辆汽车在公路上行驶,当驾驶员发现前方处设有路障,为保证安全,应在距离路障不小于处停车,设司机发现路障到踩刹车耽搁的时间忽略不计,则该车的最高行车速度不能超过多少?(结果精确到).22. 已知函数 , .(1)、 当时,求函数的值域;(2)、 对于任意 , 总存在 , 使得成立,求实数的取值范围.