广西壮族自治区北海市2023-2024学年高一上学期期末教学质量检测数学试题
试卷更新日期:2024-03-08 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 命题“ , ”的否定为( )A、 , B、., C、 , D、 ,3. 如果你正在筹划一次聚会,想知道该准备多少瓶饮料,你最希望得到所有客人需要饮料数量的( )A、四分位数 B、中位数 C、众数 D、均值4. 函数 图象大致是( )A、
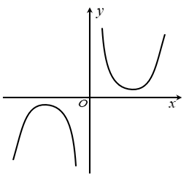 B、
B、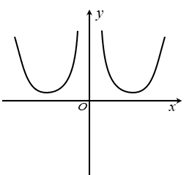 C、
C、 D、
D、 5. 已知偶函数在上单调递增,且 , 则关于的不等式的解集为( )A、 B、 C、 D、6. 已知且在内存在零点,则实数的取值范围是( )A、 B、 C、 D、7. 已知 , 则的大小关系为( )A、 B、 C、 D、8. 已知实数 , 则的最小值是( )A、1 B、 C、2 D、
5. 已知偶函数在上单调递增,且 , 则关于的不等式的解集为( )A、 B、 C、 D、6. 已知且在内存在零点,则实数的取值范围是( )A、 B、 C、 D、7. 已知 , 则的大小关系为( )A、 B、 C、 D、8. 已知实数 , 则的最小值是( )A、1 B、 C、2 D、二、多选题
-
9. 下列每组函数不是同一函数的是( )A、 B、 C、 D、10. 今年“五一”假期,各大商业综合体、超市等纷纷抓住节日商机,积极开展各类促销活动.在某超市购买80元以上商品的顾客可以参加一次抽奖活动,若顾客小王中奖的概率为0.4,顾客小张中奖的概率为0.2,则( )A、小王和小张都中奖的概率为0.08 B、小王和小张都没有中奖的概率为0.46 C、小王和小张中只有一个人中奖的概率为0.44 D、小王和小张中至多有一个人中奖的概率为0.9211. 下列命题中正确的是( )A、“”是“”的必要不充分条件 B、“且”是“”的充分不必要条件 C、“”是“”的充要条件 D、“”是“”的充要条件12. 已知函数若互不相等的实数满足 , 则的值可以是( )A、 B、 C、 D、
三、填空题
-
13. 某高中共有学生1000人,其中高一和高二各有400人,现采用分层抽样的方法抽取容量为25的样本,那么高二抽取的人数为.14. 某公司在甲、乙两地销售同一种农产品,利润(单位:万元)分别为 , ,其中 为销售量(单位:吨).若该公司在这两地共销售10吨农产品,则能获得的最大利润为万元.15. 从分别写有的7张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数字大于第二卡片上的数字的概率为.16. 若函数在上单调递减,则实数的取值范围为.
四、解答题
-
17. 设集合.求:(1)、;(2)、.18. 计算:(1)、;(2)、.19. 已知函数 ( 且 ).(1)、求关于 的不等式 的解集;(2)、若函数 在区间 上的最大值和最小值之和为 ,求实数 的值.20. 已知幂函数既不是奇函数,也不是偶函数.(1)、求的值;(2)、若函数的最小值为 , 求实数的值.21. 居民小区物业服务联系着千家万户,关系着居民的“幸福指数”.某物业公司为了调查小区业主对物业服务的满意程度,以便更好地为业主服务,随机调查了100名业主,根据这100名业主对物业服务的满意程度给出评分,分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示的频率分布直方图.
 (1)、在这100名业主中,求评分在区间[70,80)的人数与评分在区间[50,60)的人数之差;(2)、估计业主对物业服务的满意程度给出评分的众数和90%分位数;(3)、若小区物业服务满意度(满意度=)低于0.8,则物业公司需要对物业服务人员进行再培训.请根据你所学的统计知识,结合满意度,判断物业公司是否需要对物业服务人员进行再培训,并说明理由.(同一组中的数据用该区间的中点值作代表)22. 已知函数f(x)=是定义在R上的奇函数.(1)、求实数a的值;(2)、证明:函数f(x)在R上单调递增;(3)、记 , 对x∈R,不等式恒成立,求实数m的取值范围.
(1)、在这100名业主中,求评分在区间[70,80)的人数与评分在区间[50,60)的人数之差;(2)、估计业主对物业服务的满意程度给出评分的众数和90%分位数;(3)、若小区物业服务满意度(满意度=)低于0.8,则物业公司需要对物业服务人员进行再培训.请根据你所学的统计知识,结合满意度,判断物业公司是否需要对物业服务人员进行再培训,并说明理由.(同一组中的数据用该区间的中点值作代表)22. 已知函数f(x)=是定义在R上的奇函数.(1)、求实数a的值;(2)、证明:函数f(x)在R上单调递增;(3)、记 , 对x∈R,不等式恒成立,求实数m的取值范围.