贵州省贵阳市2023-2024学年高一（上）期末数学试卷

试卷更新日期：2024-03-08 类型：期末考试

进入出卷网下载

一、选择题

1. 全集 $U = {0，1 ， 2，3 ， 4，5 ， 6，7}$ ，集合 $M = {0，1 ， 2，3}$ ， $N = {3，4 ， 5}$ ， $U$ ， $M$ ， $N$ 的关系如图所示，则图中阴影部分表示的集合为（）

A、 ${1，2 ， 3，4 ， 5}$ B、 ${4，5}$ C、 ${3}$ D、 $⌀$

查看试题解析
2. 命题“ $\exists x \in R ， x^{2} + x + 1 \geq 0$ ”的否定是（）

A、 $\exists x \notin R ， x^{2} + x + 1 \geq 0$ B、 $\exists x \in R ， x^{2} + x + 1 < 0$ C、 $\forall x \in R ， x^{2} + x + 1 < 0$ D、 $\forall x \notin R ， x^{2} + x + 1 < 0$

查看试题解析
3. 对任意角 $α$ 和 $β$ ， “ $s i n α = s i n β$ ”是“ $α = β$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 已知函数 $f (x) = \frac{2}{4 x - 3} + l o g_{0.5} (2 - x)$ ，则 $f (x)$ 的定义域为（）

A、 $(\frac{3}{4} ， 2)$ B、 $(\frac{3}{4} ， 2]$ C、 $(- \infty ， 2)$ D、 $(- \infty ， \frac{3}{4}) \cup (\frac{3}{4} ， 2)$

查看试题解析
5. 函数 $f (x) = 2^{x} + x$ 的零点所在的区间为（）

A、 $(- 2 ， - 1)$ B、 $(- 1，0)$ C、 $(0，1)$ D、 $(1，2)$

查看试题解析
6. 设 $a = {(\frac{1}{2})}^{\frac{1}{2}} ， b = 2^{\frac{1}{5}} ， c = l o g_{2} \frac{1}{5}$ ，则 $a ， b ， c$ 的大小关系为（）

A、 $c < a < b$ B、 $c < b < a$ C、 $a < b < c$ D、 $a < c < b$

查看试题解析
7. 下列选项中，与 $s i n (- \frac{11 π}{6})$ 的值相等的是（）

A、 $2 s i n 15 ° s i n 75 °$ B、 $c o s 18 ° c o s 42 ° - s i n 18 ° s i n 42 °$ C、 $2 c o s^{2} 15 ° - 1$ D、 $\frac{t a n 22.5 °}{1 - t a n^{2} 22.5 °}$

查看试题解析
8. 某池塘野生水葫芦的覆盖面积与时间的函数关系图象如图所示．假设其函数关系为指数函数，其中说法错误的是（）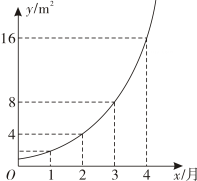

A、此指数函数的底数为2 B、在第5个月时，野生水葫芦的覆盖面积会超过 $30 m^{2}$ C、野生水葫芦从 $4 m^{2}$ 蔓延到 $12 m^{2}$ 只需1.5个月 D、设野生水葫芦蔓延至 $2 m^{2} ， 3 m^{2} ， 6 m^{2}$ 所需的时间分别为 $x_{1} ， x_{2} ， x_{3}$ ，则有 $x_{1} + x_{2} = x_{3}$

查看试题解析
9. 已知 $a$ ， $b$ ， $c \in R$ ，则下列命题正确的是（）

A、若 $\frac{1}{a} > \frac{1}{b}$ ，则 $a < b$ B、若 $a c^{2} > b c^{2}$ ，则 $a > b$ C、若 $a < b$ ， $c < d$ ，则 $a - c < b - d$ D、若 $a > b > 0$ ， $c > 0$ ，则 $\frac{a}{b} > \frac{a + c}{b + c}$

查看试题解析
10. 下列说法中，正确的是（）

A、函数 $y = \frac{1}{x}$ 在定义域上是减函数 B、函数 $y = \frac{e^{x} - 1}{e^{x} + 1}$ 是奇函数 C、函数 $y = f (x + a) - b$ 为奇函数，则函数 $y = f (x)$ 的图象关于点 $P (a ， b)$ 成中心对称图形 D、函数 $f (x)$ 为定义在 $(- \infty ， 0) \cup (0 ， + \infty)$ 上的奇函数，且 $f (3) = 1$ ，对于任意 $x_{1}$ ， $x_{2} \in (0 ， + \infty)$ ， $x_{1} \neq x_{2}$ ，都有 $\frac{x_{1} f (x_{1}) - x_{2} f (x_{2})}{x_{1} - x_{2}} > 0$ 成立，则 $f (x) \leq \frac{3}{x}$ 的解集为 $(- \infty ， - 3] \cup (0$ ， $3]$

查看试题解析

二、非选择题

11. 幂函数 $f (x) = (m^{2} - 2 m - 2) x^{m}$ 在区间 $(0 ， + \infty)$ 上单调递增，则实数 $m$ 的值为．

查看试题解析
12. 函数 $y = sin x + cos x$ 的最大值是．

查看试题解析
13. 已知圆和四边形（四个角均为直角）的周长相等，面积分别为 $S_{1}$ ， $S_{2}$ ，则 $\frac{S_{1}}{S_{2}}$ 的最小值为.

查看试题解析
14. 已知函数 $f (x) = 2 s i n (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 的部分图像如图所示，则 $f (\frac{π}{3}) =$ ．

查看试题解析
15. 已知函数 $f (x) = 2 k x^{2} - k x - \frac{3}{8} (0 \leq x \leq 2 ， k \in R)$ ，若 $k = 1$ ，则该函数的零点为 $.$ 若对 $\forall x \in [0，2]$ ，不等式 $f (x) < - 2 k$ 恒成立，则实数 $k$ 的取值范围为．

查看试题解析

三、解答题

16. 已知角 $θ$ 的终边过点 $(- 3，4)$ ，求角 $θ$ 的三个三角函数值．

查看试题解析
17.

(1)、已知 $a^{\frac{1}{2}} + a^{- \frac{1}{2}} = 3$ ，求 $a + a^{- 1}$ 的值；

(2)、已知 ${l o g}_{2} [{l o g}_{3} ({l o g}_{4} x)] = 0$ ，求 $x$ 的值．

查看试题解析
18. 已知函数 $f (x) = x - \frac{1}{x}$ ．

(1)、判断函数 $f (x)$ 的奇偶性；

(2)、根据定义证明函数 $f (x) = x - \frac{1}{x}$ 在区间 $(0 ， + \infty)$ 上单调递增．

查看试题解析
19. 将函数 $f (x) = c o s (x + \frac{π}{3})$ 的图象上所有点的横坐标缩短到原来的 $\frac{1}{2}$ ，纵坐标不变，得到函数 $g (x)$ 的图象．

(1)、求函数 $g (x)$ 的单调递增区间和对称中心；

(2)、若关于 $x$ 的方程 $2 s i n^{2} x - m c o s x - 4 = 0$ 在 $x \in (0 ， \frac{π}{2})$ 上有实数解，求实数 $m$ 的取值范围．

查看试题解析
20. $《$ 见微知著 $》$ 谈到：从一个简单的经典问题出发，从特殊到一般，由简单到复杂：从部分到整体，由低维到高维，知识与方法上的类比是探索发展的重要途径，是思想阀门发现新问题、新结论的重要方法．
阅读材料一：利用整体思想解题，运用代数式的恒等变形，使不少依照常规思路难以解决的问题找到简便解决方法，常用的途径有： $(1)$ 整体观察： $(2)$ 整体设元； $(3)$ 整体代入： $(4)$ 整体求和等．
例如， $a b = 1$ ，求证： $\frac{1}{1 + a} + \frac{1}{1 + b} = 1$ ．
证明：原式 $= \frac{a b}{a b + a} + \frac{1}{1 + b} = \frac{b}{b + 1} + \frac{1}{1 + b} = 1$ ．
阅读材料二：解决多元变量问题时，其中一种思路是运用消元思想将多元问题转化为一元问题，再结合一元问题处理方法进行研究．
例如，正实数 $a$ ， $b$ 满足 $a b = 1$ ，求 $\frac{a + b}{(1 + a) b}$ 的最小值．
解：由 $a b = 1$ ，得 $b = \frac{1}{a}$ ， $∴ \frac{a + b}{(1 + a) b} = \frac{a + \frac{1}{a}}{(1 + a) \frac{1}{a}} = \frac{a^{2} + 1}{a + 1} = \frac{(a + 1)^{2} - 2 (a + 1) + 2}{a + 1} = (a + 1) + \frac{2}{a + 1} - 2 \geq 2 \sqrt{(a + 1) \frac{2}{a + 1}} - 2 = 2 \sqrt{2} - 2$ ，
当且仅当 $a + 1 = \sqrt{2}$ ，即 $a = \sqrt{2} - 1 ， b = \sqrt{2} + 1$ 时，等号成立 $. ∴ \frac{a + b}{(1 + a) b}$ 的最小值为 $2 \sqrt{2} - 2$ ．
波利亚在 $《$ 怎样解题 $》$ 中指出：“当你找到第一个蘑菇或作出第一个发现后，再四处看看，他们总是成群生长”类似问题，我们有更多的式子满足以上特征．
结合阅读材料解答下列问题：

(1)、已知 $a b = 1$ ，求 $\frac{1}{1 + a^{2}} + \frac{1}{1 + b^{2}}$ 的值；

(2)、若正实数 $a$ ， $b$ 满足 $a b = 1$ ，求 $M = \frac{1}{1 + a} + \frac{1}{1 + 3 b}$ 的最小值．

查看试题解析