湖南省张家界市2023-2024学年高一上学期期末联考数学试题

试卷更新日期：2024-03-08 类型：期末考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知集合 $A = {3 ， 4 ， 5}$ ， $B = {y | y = 2 x - 3 ， x \in A}$ ，则 $A ∩ B =$ （）

A、 ${3}$ B、 ${4}$ C、 ${5}$ D、 ${3 ， 5}$

查看试题解析
2. 命题“ $\forall x \in (1 ， + \infty)$ ， $x - 1 > l n x$ ”的否定是（）

A、 $\exists x \in (1 ， + \infty)$ ， $x - 1 > l n x$ B、 $\exists x \in (1 ， + \infty)$ ， $x - 1 \leq l n x$ C、 $\exists x \in (1 ， + \infty)$ ， $x - 1 < l n x$ D、 $\forall x \in (1 ， + \infty)$ ， $x - 1 \leq l n x$

查看试题解析
3. 已知扇形的半径为3，圆心角弧度数为2，则其面积为（）

A、18 B、12 C、9 D、6

查看试题解析
4. 下列命题为真命题的是（）

A、若 $a > b$ ，则 $a^{2} > b^{2}$ B、若 $a > b$ ，则 $a c > b c$ C、若 $a > b$ ， $c > d$ ，则 $a + c > b + d$ D、若 $a > b$ ， $c > d$ ，则 $a c > b d$

查看试题解析
5. 学校先举办了一次田径运动会，某班有8名同学参赛，又举办了一次球类运动会，这个班有12名同学参赛，两次运动会都参赛的有3人。两次运动会中，这个班总共参赛的同学有（）

A、20人 B、17人 C、15人 D、12人

查看试题解析
6. 为了预防流感，某学校对教室采用药熏消毒法进行消毒.已知在药熏过程中，室内每立方米空气中的含药量y（单位：mg）与时间t（单位：h）的关系如图所示，函数关系式为 $y = {\begin{array}{l} 10 t ， 0 \leq t \leq 0.1 \\ {(\frac{1}{16})}^{t - a} ， t > 0.1 \end{array}$ （a为常数）.据测定，当室内每立方米空气中的含药量降到0.25mg以下时，学生方可进教室.从药熏开始，至少经过 $t_{0}$ 小时后，学生才能回到教室，则（）

A、 $a = 0.2$ ， $t_{0} = 0.6$ B、 $a = 0.2$ ， $t_{0} = 0.5$ C、 $a = 0.1$ ， $t_{0} = 0.6$ D、 $a = 0.1$ ， $t_{0} = 0.5$

查看试题解析
7. 英国数学家泰勒（B.Taylor，1685—1731）发现了如下公式： $s i n x = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} + \cdot \cdot \cdot$ ， $c o s x = 1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} + \cdot \cdot \cdot$ ，其中 $n! = 1 \times 2 \times 3 \times 4 \times \cdot \cdot \cdot \times n$ .这些公式被编入计算工具，计算工具计算足够多的项就可以确保显示值的精确性，计算器使用的这种方法叫数值计算法.比如，用前三项计算 $c o s 0.3$ ，就得到 $c o s 0.3 \approx 1 - \frac{0 . 3^{2}}{2!} + \frac{0 . 3^{4}}{4!} = 0.9553375$ .运用上述思想，可得到 $s i n 1$ 的近似值为（）

A、0.83 B、0.84 C、0.85 D、0.86

查看试题解析
8. 若 $a = c o s 50 ° c o s 128 ° + c o s 40 ° c o s 38 °$ ， $b = \frac{\sqrt{2}}{2} (s i n 56 ° - c o s 56 °)$ ， $c = \frac{1 - t a n^{2} 40 ° 3 0^{'}}{1 + t a n^{2} 40 ° 3 0^{'}}$ ， $d = \frac{1}{2} (c o s 80 ° - 2 c o s^{2} 50 ° + 1)$ ，则a，b，c，d的大小关系为（）

A、 $a > b > d > c$ B、 $b > a > d > c$ C、 $d > a > b > c$ D、 $c > a > d > b$

查看试题解析

二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 下列各命题中，p是q的充要条件的有（）

A、p：两个三角形相似；q：两个三角形三边成比例 B、p：四边形是菱形； $q$ ：四边形的对角线互相垂直 C、 $p$ ： $x y > 0$ ； $q$ ： $x > 0$ ， $y > 0$ D、 $p$ ： $l g x > 1$ ； $q$ ： $x > 10$

查看试题解析
10. 函数y＝3sin $(2 x + \frac{π}{3})$ 的图象，可由函数y＝sin x的图象经过下列哪项变换而得到（）

A、向左平移 $\frac{π}{3}$ 个单位长度，横坐标伸长到原来的2倍，纵坐标伸长到原来的3倍 B、向左平移 $\frac{π}{3}$ 个单位长度，横坐标缩短到原来的 $\frac{1}{2}$ ，纵坐标伸长到原来的3倍 C、横坐标缩短到原来的 $\frac{1}{2}$ ，向左平移 $\frac{π}{3}$ 个单位长度，纵坐标伸长到原来的3倍 D、横坐标缩短到原来的 $\frac{1}{2}$ ，向左平移 $\frac{π}{6}$ 个单位长度，纵坐标伸长到原来的3倍

查看试题解析
11. 已知函数 $f (x) = a^{x} - {(\frac{1}{a})}^{x}$ ，其中 $a > 0$ ，且 $a \neq 1$ ，则下列结论中正确的是（）

A、函数 $f (x)$ 是奇函数 B、函数 $f (x)$ 在其定义域上有零点 C、函数 $f (x)$ 的图象过定点 $(0 ， 1)$ D、当 $a > 1$ 时，函数 $f (x)$ 在其定义域上单调递增

查看试题解析
12. 已知函数 $f (x)$ 的定义域为 $R$ ，则下面判断正确的是（）

A、若 $\forall x \in R$ ， $f (x + 1) > f (x)$ ，则函数 $f (x)$ 在 $R$ 上是增函数 B、若 $\forall x_{1} ， x_{2} \in R$ ， $| f (x_{1}) + f (x_{2}) | \leq | s i n x_{1} + s i n x_{2} |$ ，则函数 $f (x)$ 是奇函数 C、若 $\forall x_{1} ， x_{2} \in R$ ， $| f (x_{1}) - f (x_{2}) | \leq | s i n x_{1} - s i n x_{2} |$ ，则函数 $f (x)$ 是周期函数 D、若 $\forall x_{1} ， x_{2} \in (- 1 ， 1)$ 且 $x_{1} \neq x_{2}$ ， $| f (x_{1}) - f (x_{2}) | < | s i n x_{1} - s i n x_{2} |$ ，则函数 $f (x) - s i n x$ 在区间 $(- 1 ， 1)$ 上单调递增，函数 $f (x) + s i n x$ 在区间 $(- 1 ， 1)$ 上单调递减

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分.

13. 写出一个同时具有下列性质①②的函数 $f (x)$ ：.
① $f (x)$ 是偶函数；② $f (x)$ 在 $(0 ， + ∞)$ 上是增函数.

查看试题解析
14. 若 $a > 0$ ， $b > 0$ ， $a + b = 1$ ，则 $\frac{1}{a} + \frac{1}{b}$ 的最小值为.

查看试题解析
15. 17世纪德国著名的天文学家、数学家约翰尼斯·开普勒（JohannesKepler）曾经这样说过：“几何学里有两件宝，一个是勾股定理，另一个是黄金分割.如果把勾股定理比作黄金矿的话，那么可以把黄金分割比作钻石矿.”黄金三角形有两种，其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形，它是一个顶角为36°的等腰三角形（另一种是顶角为108°的等腰三角形）.例如，五角星由五个黄金三角形与一个正五边形组成，如图，在其中一个黄金 $△ A B C$ 中， $\frac{B C}{A C} = \frac{\sqrt{5} - 1}{2}$ ，根据这些信息，可得 $s i n 954 ° =$ .

查看试题解析
16. 设函数 $f (x) = x + \frac{1}{x}$ ，若方程 $f (| 3^{x} - 2 |) + 2 a (\frac{1}{| 3^{x} - 2 |} + 1) - 3 = 0$ 有3个不等的实根，则实数 $a$ 的取值范围是.

查看试题解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. 已知集合 $A = {x | 3 \leq 3^{x} \leq 27}$ ， $B = {x | x > 2}$ .

(1)、求 $A ∪ (∁_{R} B)$ ；

(2)、已知集合 $C = {x | 1 < x < a} (a > 1)$ ，若 $C \subseteq A$ ，求实数 $a$ 的取值范围。

查看试题解析
18. 已知函数 $f (x) = m x^{2} + 2 (m + 1) x + 4$ .

(1)、若 $m = 2$ ，解不等式 $f (x) < 0$ ；

(2)、若关于 $x$ 的不等式 $f (x) < - 9 m$ 的解集为 $R$ ，求实数 $m$ 的取值范围.

查看试题解析
19. 如图，已知单位圆O与x轴正半轴交于点M，点A，B在单位圆上，其中点A在第一象限，且 $∠ A O B = \frac{π}{2}$ ，记 $∠ M O A = α$ ， $∠ M O B = β$ .

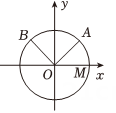(1)、若 $α = \frac{π}{3}$ ，求点 $A$ 的坐标；

(2)、若点A的坐标为 $(\frac{4}{5} ， m)$ ，求 $s i n α - s i n β$ 的值.

查看试题解析
20. 已知函数 $f (x) = \frac{m}{x^{2} + n}$ 的图象过点 $(1 ， 1)$ 和 $(2 ， \frac{1}{2})$

(1)、求 $f (x)$ 的解析式，并判断函数 $f (x)$ 的奇偶性；

(2)、判断函数 $f (x)$ 在 $(0 ， + \infty)$ 的单调性，并用单调性的定义证明.

查看试题解析
21. 一根长为L的材料 $A B$ （材料粗细忽略不计）欲水平通过如图所示的直角走廊，已知走廊的宽 $A C = B D = 1 m$ .

(1)、设 $∠ B O D = θ$ ，试将L表示为 $θ$ 的函数，并写出 $θ$ 的取值范围；

(2)、求能够通过这个直角走廊的材料的最大长度（即求L的最小值）.

查看试题解析
22. 设函数 $f (x) = c o s \frac{π}{3} x$ ， $g (x) = l n x$ ， $h (x) = e^{2 x} - \frac{2}{5} e^{x} - 1$ .

(1)、求函数 $y = f (x)$ 在 $(0 ， 6)$ 上的单调区间；

(2)、若 $\forall x_{1} \in (0 ， 3)$ ， $\exists x_{2} \in (- \infty ， a)$ ，使 $f (x_{1}) = h (x_{2})$ 成立，求实数 $a$ 的取值范围；

(3)、求证：函数 $φ (x) = f (x) - g (x)$ 在 $(0 ， + ∞)$ 上仅有一个零点 $x_{0}$ ，并求 $[h (g (x_{0}))]$ （ $[x]$ 表示不超过 $x$ 的最大整数，如 $[2.7] = 2$ ， $[- 3.2] = - 4$ ）

查看试题解析