广东省潮州市2023-2024学年高三上学期期末教学质量检测 数学
试卷更新日期:2024-03-07 类型:期末考试
一、单项选择题(本题共8道小题,每小题只有一个选项正确,每小题5分,共40分)
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 已知i为虚数单位,若复数对应的点在复平面的虚轴上,则实数( )A、 B、 C、6 D、3. 已知圆锥的侧面展开图是半径为2且面积为的扇形,则这个圆锥的底面半径为( )A、 B、 C、1 D、24. 命题“ , ”为假命题的一个充分不必要条件是( )A、 B、 C、 D、5. 已知单位向量 , 满足 , 则在方向上的投影向量为( )A、 B、 C、 D、6. 若函数在上有极值,则实数的取值范围是( )A、 B、 C、 D、7. 已知双曲线的左焦点为F,M、N,P是双曲线上的点,其中线段的中点恰为坐标原点 , 且点在第一象限,若 , , 则双曲线的离心率为( )A、 B、 C、 D、8. 已知函数满足 , 若且 , 则的值为A、 B、 C、 D、
二、多项选择题(本题共4小题,每小题5分,共20分,每小题有多个选项正确,每小题全部选对得5分,部分选对得2分,有选错得0分)
-
9. 下列说法中正确的是( )A、某射击运动员在一次训练中10次射击成绩(单位:环)如下:6,5,7,9,6,8,9,9,7,5,则这组数据的第70百分位数为8 B、若随机变量 , 且 , 则 C、若随机变量 , 且 , 则 D、对一组样本数据 , , …,进行分析,由此得到的回归方程为 , 则至少有一个数据点在回归直线上10. 已知 , , , 则( )A、 B、 C、 D、11. 设过点的直线与圆相交于A,B两点,若点 , 则的值可能为( )A、8 B、 C、12 D、12. 如图,已知正方体顶点处有一质点Q,点Q每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同.从一个顶点沿一条棱移动到相邻顶点称为移动一次.若质点Q的初始位置位于点A处,记点Q移动n次后仍在底面ABCD上的概率为 , 则下列说法正确的是( )
 A、 B、 C、点Q移动4次后恰好位于点的概率为0 D、点Q移动10次后仍在底面ABCD上的概率为
A、 B、 C、点Q移动4次后恰好位于点的概率为0 D、点Q移动10次后仍在底面ABCD上的概率为三、填空题(本题共4小题,每小题5分,共20分)
-
13. 将编号为1,2,3,4的四个小球全部放入甲、乙两个盒子内,若每个盒子不空,则不同的方法总数有种.(用数字作答)14. O为坐标原点,为抛物线的焦点,为上一点,若 , 则的面积为 .15. 设等差数列的前项和为 , 且 , , 若 , 则数列中最小项的值为 .16. 设函数 , 已知直线与函数的图象交于A、B两点,且的最小值为(e为自然对数的底),则 .
四、解答题(本题共6道小题,第17题10分,第18-22题每小题12分,共70分)
-
17. 公比为的等比数列的前项和 .(1)、求与的值;(2)、若 , 记数列的前项和为 , 求证: .18. 2023年9月26日晚,位于潮州市南春路的南门古夜市正式开业了,首期共有70个摊位,集聚了潮州各式美食!南门古夜市的开业,推动潮州菜产业发展,是潮州美食产业的又一里程碑.为了解游客对潮州美食的满意度,随机对100名游客进行问卷调查(满分100分),这100名游客的评分分别落在区间 , , , , 内,统计结果如频率分布直方图所示.
 (1)、根据频率分布直方图,求这100名游客评分的平均值(同一区间的数据用该区间数据的中点值为代表);(2)、为了进一步了解游客对潮州美食的评价,采用分层抽样的方法从满意度评分位于分组 , , 的游客中抽取10人,再从中任选3人进行调查,求抽到满意度评分位于的人数的分布列和数学期望.19. 在矩形中, , (如图1),将沿折起到的位置,使得点在平面上的射影在边上,连结(如图2).
(1)、根据频率分布直方图,求这100名游客评分的平均值(同一区间的数据用该区间数据的中点值为代表);(2)、为了进一步了解游客对潮州美食的评价,采用分层抽样的方法从满意度评分位于分组 , , 的游客中抽取10人,再从中任选3人进行调查,求抽到满意度评分位于的人数的分布列和数学期望.19. 在矩形中, , (如图1),将沿折起到的位置,使得点在平面上的射影在边上,连结(如图2).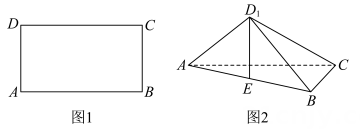 (1)、证明:;(2)、过直线的平面与平行,求平面与平面夹角的余弦值.
(1)、证明:;(2)、过直线的平面与平行,求平面与平面夹角的余弦值.