广东省深圳市2023-2024学年九年级中考适应性考试数学试题

试卷更新日期：2024-03-07 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，其中只有一个是正确的）

1. 围棋在古代被列为“琴棋书画”四大文化之一，蕴含着中华文化的丰富内涵，如图所示是一个无盖的围棋罐，其主视图为（　　）

A、 B、 C、 D、

查看试题解析
2. 已知x＝1是关于x的一元二次方程x²+kx﹣6＝0的一个根，则k的值为（　　）

A、﹣5 B、﹣7 C、5 D、7

查看试题解析
3. 如图，在菱形ABCD中，∠B＝60°，连接AC，若AC＝6，则菱形ABCD的周长为（　　）

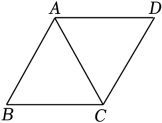A、24 B、30 C、 $18 \sqrt{3}$ D、 $36 \sqrt{3}$

查看试题解析
4. 用配方法解方程x²+2x＝3时，配方后正确的是（　　）

A、（x+2）²＝7 B、（x+2）²＝5 C、（x+1）²＝4 D、（x+1）²＝2

查看试题解析
5. 如图，在由大小相同的小正方形组成的网格中有一条“心形线”．数学小组为了探究随机投放一个点恰好落在“心形线”内部的概率，进行了计算机模拟试验，得到如下数据：
试验总次数
100
200
300
500
1500
2000
3000
落在“心形线”内部的次数
61
93
165
246
759
996
1503
落在“心形线”内部的频率
0.610
0.465
0.550
0.492
0.506
0.498
0.501
根据表中的数据，估计随机投放一点落在“心形线”内部的概率为（　　）

A、0.46 B、0.50 C、0.55 D、0.61

查看试题解析
6. 一段加固后的护栏如图所示，该护栏竖直部分是由等距（任意相邻两根木条之间的距离相等）且平行的木条构成．已知AC＝50cm，则BC的长度为（　　）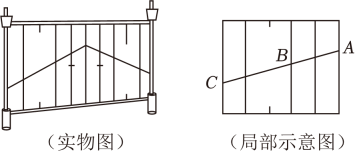

A、20cm B、25cm C、30cm D、 $\frac{100}{3}$ cm

查看试题解析
7. 击地传球是篮球运动中的一种传球方式，利用击地传球可以有效地躲避对手的拦截．传球选手从点A处将球传出，经地面点O处反弹后被接球选手在点C处接住，将球所经过的路径视为直线，此时∠AOB＝∠COD．若点A距地面的高度AB为1.5m，点C距地面的高度CD为1m，传球选手与接球选手之间的距离BD为5m，则OB的长度为（　　）

A、 $\frac{5}{3}$ m B、2m C、2.5m D、3m

查看试题解析
8. 据报道，2020年至2022年深圳市居民年人均可支配收入由6.49万元增长至7.27万元，设这两年人均可支配收入的年平均增长率为x，可列方程为（　　）

A、6.49（1+x）²＝7.27 B、6.49（1+2x）＝7.27 C、6.49（1+x²）＝7.27 D、7.27（1﹣x）²＝6.49

查看试题解析
9. 如图是凸透镜成像示意图，CD是蜡烛AB通过凸透镜MN所成的虚像．已知蜡烛的高AB为5.4cm，蜡烛AB离凸透镜MN的水平距离OB为6cm，该凸透镜的焦距OF为10cm，AE∥OF，则像CD的高为（　　）

A、15cm B、14.4cm C、13.5cm D、9cm

查看试题解析
10. 如图，在菱形ABCD中，对角线AC与BD相交于点O，过点D作DF⊥AB于点F，交AC于点E．已知AE＝4，EC＝6，则 $\frac{O E}{B F}$ 的值为（　　）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{30}}{10}$ C、 $\frac{\sqrt{10}}{10}$ D、 $\frac{\sqrt{5}}{3}$

查看试题解析

二、填空题（本大题共5小题，每小题3分，共15分）

11. 已知5a＝2b，则a：b＝．

查看试题解析
12. 为测量广场上一棵树的高度，数学小组在阳光下测得广场上一根6m高的灯柱的影长为3m，在同一时刻，他们测得树的影长为2m，则该树的高度为 m．

查看试题解析
13. 深圳某校举办了“博古通今，学史明智”的历史事件讲述大赛，选题有“鸦片战争”“香港回归”“改革开放”．八、九年级分别从中随机选择一个不同事件进行比赛，则八、九年级所选的历史事件都发生于新中国成立以后的概率为．

查看试题解析
14. 如图，在平面直角坐标系中，点A在第一象限，点B在x轴的正半轴，AO＝AB＝2，将△OAB沿OA所在的直线翻折后，点B落在点C处，且CA∥y轴，反比例函数 $y = \frac{k}{x}$ 的图象经过点C，则k的值为．

查看试题解析
15. 如图，在四边形ABCD中，AB＝BC＝6，∠ABC＝60°，∠ADC＝90°，对角线AC与BD相交于点E，若BE＝3DE，则BD＝．

查看试题解析

三、解答题（本题共7小题，共55分）

16. 解方程：x²﹣4x+3＝0．

查看试题解析
17. 深圳蕴藏丰富的旅游文化资源．为促进深港两地学生交流，某校开展“美丽深圳，深港同行”主题活动，景点有三个：A．梧桐烟云，B．莲花春早，C．梅沙踏浪．每位参加交流的学生都可以从中随机选择一个景点．

(1)、参加此次交流活动的小军选择的景点为“梧桐烟云”的概率是；

(2)、请用列表或画树状图的方法，求小明和小颖选择的景点都是“莲花春早”的概率．

查看试题解析
18. 已知一个矩形的面积为6，长为x，宽为y．

(1)、y与x之间的函数表达式为；

(2)、在图中画出该函数的图象；
列表：
x
…
1
2
3
4
6
…
y
…
6
3
m
1.5
1
…
上面表格中m的值是 ▲ ；
描点：在如图所示的平面直角坐标系中描出相应的点；
连线：用光滑的曲线顺次连接各点，即可得到该函数的图象．

(3)、若点A（a，b）与点B（a+1，c）是该函数图象上的两点，试比较b和c的大小．

查看试题解析
19. 某品牌画册每本成本为40元，当售价为60元时，平均每天的销售量为100本．为了吸引消费者，商家决定采取降价措施．经试销统计发现，如果画册售价每降低1元时，那么平均每天就能多售出10本．设这种画册每本降价x元．

(1)、平均每天的销售量为本（用含x的代数式表示）；

(2)、商家想要使这种画册的销售利润平均每天达到2240元，且要求每本售价不低于55元，求每本画册应降价多少元？

查看试题解析
20. 如图，点O是矩形ABCD的对角线AC上一点，过点O作EF⊥AC，交BC于点E，交AD于点F．

(1)、在不添加新的点和线的前提下，请增加一个条件： ▲ ，使得OE＝OF，并说明理由；

(2)、若OE＝OF，AB＝6，BC＝8，求EF的长．

查看试题解析
21. 【项目式学习】
项目主题：守护生命，“数”说安全．
项目背景：随着社会的发展，安全问题变得日益重要．某校为了提高学生的安全意识，开展以“守护生命，'数'说安全”为主题的项目式学习活动．创新小组通过考察测量、模拟探究和成果迁移等环节，开展地下弯道对通行车辆长度的限制研究．

(1)、任务一：考察测量
如图1，创新小组所选取弯道的内、外侧均为直角，道路宽均为4m，则AB＝m；

(2)、任务二：模拟探究
如果汽车在行驶中与弯道内、外侧均无接触，则可安全通过．
创新小组用线段模拟汽车通过宽度相同的直角弯道，探究发现：
①当CD＜2AB时（如图1），线段CD能通过直角弯道；
②当CD＝2AB时，必然存在线段CD的中点E与点B重合的情况，线段CD恰好不能通过直角弯道（如图2）．此时，∠ADC的度数是；③当CD＞2AB时，线段CD不能通过直角弯道．

(3)、如图3，创新小组用矩形PQMN模拟汽车通过宽均为4m的直角弯道，发现当PQ的中点E与点B重合，且PQ⊥AB时，矩形PQMN恰好不能通过该弯道．若PQ＝am，PN＝2m，且矩形PQMN能通过该直角弯道，求a的最大整数值．

(4)、任务三：成果迁移
如图4，某弯道外侧形状可近似看成反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象，其对称轴交图象于点A．弯道内侧的顶点B在射线OA上，两边分别与x轴，y轴平行，OA＝2m，AB＝4 $\sqrt{2}$ m．创新小组探究发现通过该弯道的原理与通过直角弯道类似．有一辆长为bm，宽为2m的汽车需要安全通过该弯道，则b的最大整数值为．（参考数据： $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7， $\sqrt{5}$ ≈2.2， $\sqrt{7}$ ≈2.6）

查看试题解析
22. 已知点E是正方形ABCD内部一点，且∠BEC＝90°．

(1)、【初步探究】
如图1，延长CE交AD于点P．求证：△BEC∽△CDP；

(2)、【深入探究】
如图2，连接DE并延长交BC于点F，当点F是BC的中点时，求 $\frac{C E}{B E}$ 的值；

(3)、【延伸探究】
连接DE并延长交BC于点F，DF把∠BEC分成两个角，当这两个角的度数之比为1：2时，请直接写出 $\frac{C E}{B E}$ 的值．

查看试题解析

试验总次数	100	200	300	500	1500	2000	3000
落在“心形线”内部的次数	61	93	165	246	759	996	1503
落在“心形线”内部的频率	0.610	0.465	0.550	0.492	0.506	0.498	0.501

x	…	1	2	3	4	6	…
y	…	6	3	m	1.5	1	…