广东省深圳市2024年数学中考复习综合检测模拟试卷

试卷更新日期：2024-03-07 类型：中考模拟

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 2024年1月1日，某地4个时刻的气温（单位：℃）分别为﹣4，0，1，﹣3，其中最低的气温是（　　）

A、﹣4 B、0 C、1 D、﹣3

查看试题解析
2. 下列图形中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 如图，四个大小相同的正方体搭成的几何体，从正面看得到的图形是（　　）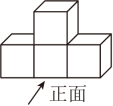

A、 B、 C、 D、

查看试题解析
4. 若x＝1是方程x²﹣mx+3＝0的一个根，则m＝（　　）

A、3 B、4 C、﹣3 D、﹣4

查看试题解析
5. 如图，有一路灯杆AP，路灯P距地面4.8m，身高1.6m的小明站在距A点4.8m的点D处，小明的影子为DE，他沿射线DA走2.4m到达点B处，小明的影子为BC，此时小明影子的长度（）

A、增长了1m B、缩短了1m C、增长了1.2m D、缩短了1.2m

查看试题解析
6. 如图，四边形 $A B C D$ 为菱形， $A B = 4$ ， $∠ A = 60 °$ ，则 $B D$ 的长为（）

A、2 B、4 C、 $\frac{4}{3} \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
7. 在学习了“用频率估计概率”这一节内容后，某课外兴趣小组利用计算器进行模拟试验来探究“6个人中有2个人同月过生日的概率”，他们将试验中获得的数据记录如下：
试验次数
100
300
500
1000
1600
2000
“有2个人同月过生日”的次数
80
229
392
779
1251
1562
“有2个人同月过生日”的频率
0.8
0.763
0.784
0.779
0.782
0.781
通过试验，该小组估计“6个人中有2个人同月过生日”的概率（精确到0.01）大约是（　　）

A、0.8 B、0.784 C、0.78 D、0.76

查看试题解析
8. 在同一平面直角坐标系中，一次函数y＝kx+k与反比例函数y＝ $\frac{k}{x}$ （k为常数，k≠0）的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
9. 电影《志愿军：雄兵出击》于2023年9月28日上映，首周票房约 $2.5$ 亿，第三周票房约 $3.6$ 亿，若每周票房按相同的增长率增长，设增长率为 $x$ ，则根据题意可列方程为（）

A、 $2.5 (1 + x) = 3.6$ B、 $2.5 {(1 + x)}^{2} = 3.6$ C、 $2.5 + 2.5 (1 + x) = 3.6$ D、 $2.5 + 2.5 (1 + x) + 2.5 {(1 + x)}^{2} = 3.6$

查看试题解析
10. 如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D是 $\overset{⌢}{B C}$ 的中点，AD交BC于点E，若CE＝ $\frac{\sqrt{2}}{2}$ ，BE＝ $\frac{3 \sqrt{2}}{2}$ ，以下结论中：①sin∠ABC＝ $\frac{1}{3}$ ；②AD＝ $\sqrt{6}$ ，③S_⊙_O＝ $\frac{9}{4}$ π；④OE∥BD.其中正确的共有（）个.

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（共5小题，满分15分，每小题3分）

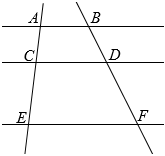
11. 分解因式：2x²﹣8x+8=

查看试题解析
12. 若一组数据1，3，x，5，4，6的平均数是4，则这组数据的中位数是.

查看试题解析
13. 如图，AB∥CD∥EF，若AC＝2，CE＝5，BD＝3，则DF＝．

查看试题解析
14. 如图，在平面直角坐标系中，直线AB与x轴交于点 $A (- 2 \sqrt{3} ， 0)$ ，与x轴夹角为30°，将△ABO沿直线AB翻折，点O的对应点C恰好落在双曲线 $y = \frac{k}{x} (k \neq 0)$ 上，则k＝．

查看试题解析
15. 如图，在等边三角形ABC中，D是AC的中点，P是边AB上的一个动点，过点P作PE⊥AB，交BC于点E，连接DP，DE.若AB＝8，△PDE是等腰三角形，则BP的长是.

查看试题解析

三、解答题（共7小题，满分55分）

16. 计算：2cos²45°﹣1+tan30°tan60°．

查看试题解析
17. 先化简再求值（x+1﹣ $\frac{3}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x - 1}$ ，再从1，2，3中选取一个适当的数代入求值．

查看试题解析
18. 为提高居民防范电信网络诈骗的意识，某社区举办相关知识比赛．现从该社区甲、乙两个参赛代表队中各随机抽取10名队员的比赛成绩，并进行整理、描述和分析（分数用x表示，共分为四组：A.60≤x＜70，B.70≤x＜80，C.80≤x＜90，D．x≥90）．
下面给出了部分信息：
甲队10名队员的比赛成绩：69，79，88，90，92，94，94，96，98，100．
乙队10名队员的比赛成绩在D组中的所有数据为：92，92，97，99，99，99．
甲、乙代表队中抽取的队员比赛成绩统计表
代表队
平均数
中位数
众数
“C”组所占百分比
甲
90
a
94
10%
乙
90
92
b
20%
根据以上信息，解答下列问题：

(1)、填空：a＝， b＝， m＝；

(2)、该社区甲代表队有200名队员、乙代表队有230名队员参加了此次比赛，估计此次比赛成绩在A组的队员共有多少名；

(3)、根据以上数据，你认为甲、乙哪个代表队的比赛成绩更好？请说明理由（写出一条理由即可）．

查看试题解析
19. 住宅的采光是建楼和购房时人们所关心的问题之一．如图，住宅小区南、北两栋楼房的高度均为16.8m．已知当地冬至这天中午12时太阳光线与地面所成的角是35°．（参考数据：sin35°≈0.57；cos35°≈0.81；tan35°≈0.70）

(1)、要使这时南楼的影子恰好落在北楼的墙脚，两楼间的距离应为多少米（精确到0.1m）？

(2)、如果两栋楼房之间的距离为20m，那么这时南楼的影子是否会影响北楼一楼的采光（忽略其他影响采光的因素）？

查看试题解析
20. 在长方形纸片ABCD中，点E是边CD上的一点，将△AED沿AE所在的直线折叠，使点D落在点F处.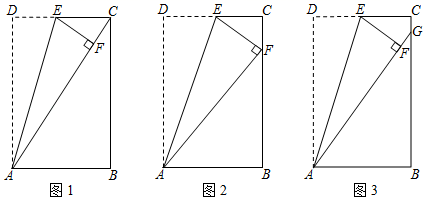

(1)、如图1，若点F落在对角线AC上，且∠BAC＝54°，则∠DAE的度数为°.

(2)、如图2，若点F落在边BC上，且AB＝6，AD＝10，求CE的长.

(3)、如图3，若点E是CD的中点，AF的沿长线交BC于点G，且AB＝6，AD＝10，求CG的长.

查看试题解析
21. 如图，AB为⊙O直径，C，D为⊙O上的两点，且∠ACD＝2∠A，CE⊥DB交DB的延长线于点E．

(1)、求证：CE是⊙O的切线；

(2)、若DE＝2CE，AC＝4，求⊙O的半径．

查看试题解析
22. 在平面直角坐标系中，抛物线y＝﹣x²+bx+c（b，c是常数）与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C．P为x轴上方抛物线上的动点（不与点C重合），设点P的横坐标为m．

(1)、直接写出b，c的值；

(2)、如图，直线l是抛物线的对称轴，当点P在直线l的右侧时，连接PA，过点P作PD⊥PA，交直线l于点D．若PA＝PD，求m的值；

(3)、过点P作x轴的平行线与直线BC交于点Q，线段PQ的长记为d．
①求d关于m的函数解析式；
②根据d的不同取值，试探索点P的个数情况．

查看试题解析

试验次数	100	300	500	1000	1600	2000
“有2个人同月过生日”的次数	80	229	392	779	1251	1562
“有2个人同月过生日”的频率	0.8	0.763	0.784	0.779	0.782	0.781

代表队	平均数	中位数	众数	“C”组所占百分比
甲	90	a	94	10%
乙	90	92	b	20%