广东省深圳市龙华区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-03-07 类型：期末考试

进入出卷网下载

一、选择题（本题共有10小题，每小题3分，共30分，每小题有四个选项，其中只有一个是正确的）

1. 无理数最早由毕达哥拉斯学派弟子希伯索斯发现。下列各数是无理数的是（）

A、0 B、 $\sqrt{2}$ C、 $- \frac{1}{3}$ D、3. 3

查看试题解析
2. 如图是某学校的示意图，以办公楼所在位置为原点，以图中小正方形的边长为单位长度，建立平面直角坐标系，则教学楼的坐标是（）

A、 $(2 ， 4)$ B、 $(- 2 ， 4)$ C、 $(- 2 ， - 4)$ D、 $(2 ， - 4)$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} - \sqrt{2} = 1$ C、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ D、 $\sqrt{3} \div \sqrt{2} = \frac{3}{2}$

查看试题解析
4. 某商店销售5种领口大小（单位： $c m$ ）分别为38，39，40，41，42的衬衫. 为了调查各种领口大小衬衫的销售情况，商店统计了某天的销售情况，并绘制了如图的扇形统计图. 你认为该商店应多购进的衬衫的领口大小为（）

A、 $38 c m$ B、 $39 c m$ C、 $40 c m$ D、 $41 c m$

查看试题解析
5. 大、中、小三个正方形摆放如图所示，若大正方形的面积为5，小正方形的面积为1，则中正方形 $A B C D$ 的边长可能是（）

A、1 B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、3

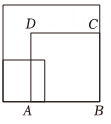查看试题解析
6. 某次数学综合实践课上，小明将一副三角板摆成如图4所示的样子，则 $∠ 1$ 的大小为（）

A、 $7 0^{∘}$ B、 $7 5^{∘}$ C、 $8 0^{∘}$ D、 $8 5^{∘}$

查看试题解析
7. 小华新买了一条跳绳，如图1，他按照体育老师教的方法确定适合自己的绳长：一脚踩住绳子的中央，手肘靠近身体，两肘弯屈 $9 0^{∘}$ ，小臂水平转向两侧，两手将绳拉直，绳长即合适长度。将图1抽象成如图2，若两手握住的绳柄两端距离约为1米，小臂到地面的距离约1. 2米，则适合小华的绳长为（）

A、2. 2米 B、2. 4米 C、2. 6米 D、2. 8米

查看试题解析
8. 《九章算术》“盈不足”章第五题：今有共买金，人出四百，盈三千四百；人出三百，盈一百。问人数、金价各是多少？题目大意：几个人合伙买金，每人出400钱，会多出3400钱；每人出300钱，会多出100钱。合伙人数、金价各是多少？设合伙人数为 $x$ 人，金价为 $y$ 钱，则下列方程组正确的是（）

A、 ${\begin{array}{l} 400 x + 3400 = y \\ 300 x + 100 = y \end{array}$ B、 ${\begin{array}{l} 400 x - 3400 = y \\ 300 x + 100 = y \end{array}$ C、 ${\begin{array}{l} 400 x + 3400 = y \\ 300 x - 100 = y \end{array}$ D、 ${\begin{array}{l} 400 x - 3400 = y \\ 300 x - 100 = y \end{array}$

查看试题解析
9. 一次函数 $y = k x + b$ 与 $y = m x + n$ 的图象如图所示，则下列说法不正确的是（）

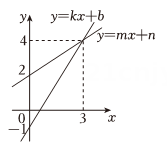A、 $b = - 1 ， n = 2$ B、这两个函数的图象与 $y$ 轴围成的三角形的面积为4. 5 C、关于 $x ， y$ 的方程组 ${\begin{array}{l} y = k x + b \\ y = m x + n \end{array}$ 的解为 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ D、当 $x$ 从0开始增加时，函数 $y = k x + b$ 比 $y = m x + n$ 的值先达到3

查看试题解析
10. 如图，在 $△ A B C$ 中，点 $D ， E ， F$ 分别在边 $A B ， B C ， A C$ 上，连接 $D E ， D F$ ，已知 $△ A B C$ ， $△ A D F$ ， $△ B D E$ 都是等边三角形，点 $M ， N$ 分别是 $A F ， D E$ 的中点，连接 $M N$ ，当 $A D = 2 ， ∠ D N M = 4 5^{∘}$ 时， $B D$ 的长度为（）

A、 $2 \sqrt{3}$ B、4 C、 $3 \sqrt{2}$ D、 $2 \sqrt{5}$

查看试题解析

二、填空题（本题共有5小题，每小题3分，共15分。请把答案填在答题卷相应的表格里. ）

11. 请写出一个比 $\sqrt{3}$ 大的数：.

查看试题解析
12. 某校规定学生的体育成绩由三部分组成：体育课堂表现占成绩的 $20 %$ ，体育理论测试占 $30 %$ ，体育技能测试占 $50 %$ 。小颖的上述三项成绩依次是90分，80分，88分，则小颖这学期的体育成绩是分.

查看试题解析
13. 如图， $B D$ 为长方形 $A B C D$ 的对角线， $B E$ 平分 $∠ A B D$ ，若 $∠ B D C = 5 0^{∘}$ ，则 $∠ A E B =$ °.

查看试题解析
14. 如图，某植物 $t$ 天后的高度为 $y c m$ ， $l$ 反映了 $y$ 与 $t$ 之间的关系，则该植物平均每天长高cm.

查看试题解析
15. 如图， $△ A B C$ 和 $△ A D E$ 都是等腰直角三角形， $∠ D A E = ∠ C A B = 9 0^{∘}$ ，点 $C$ 在边 $D E$ 上， $B C$ 与 $A E$ 交于点 $F$ ，若 $C E = 1 ， D C = 3$ ，记 $△ A B F$ 的面积为 $S_{1}$ ， $△ C E F$ 的面积为 $S_{2}$ ，则 $S_{1} - S_{2} =$ .

查看试题解析

三、解答题（本题共7小题，共55分）

16. 计算：

(1)、 $\sqrt{12} + \sqrt{27} - \sqrt{3}$ ；

(2)、 $(\sqrt{18} + \sqrt{\frac{1}{2}}) \times \sqrt{8}$ .

查看试题解析
17. 解方程组： ${\begin{matrix} 2 x - y = 5 \\ x + y = 4 \end{matrix}$ ．

查看试题解析
18. 某校拟派一名跳高运动员参加一项校际比赛，对甲、乙两名跳高运动员进行了8次选拔比赛，他们的成绩（单位： $m$ ）如下：
甲： 1. 71，1. 65，1. 68，1. 68，1. 72，1. 73，1. 68，1. 67；
乙： 1. 60，1. 74，1. 72，1. 69，1. 62，1. 71，1. 69，1. 75；

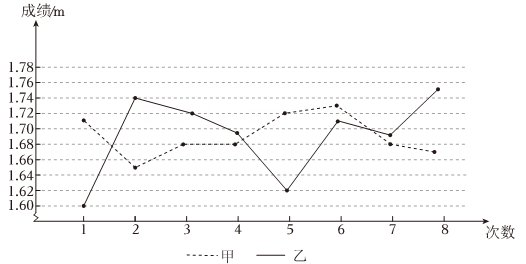(1)、【整理与分析】
平均数众数中位数
甲 1.69 a 1.68
乙 1.69 1.69 b

①由上表填空： $a =$ ， $b =$ ；
②这两人中，的成绩更为稳定。

(2)、【判断与决案】
经预测，跳高 $1.69 m$ 就很可能获得冠军，该校为了获取跳高比赛冠军，可能选哪位运动员参赛？请说明理由。

查看试题解析
19. 已知一次函数 $y = 2 x + 4$ ，请回答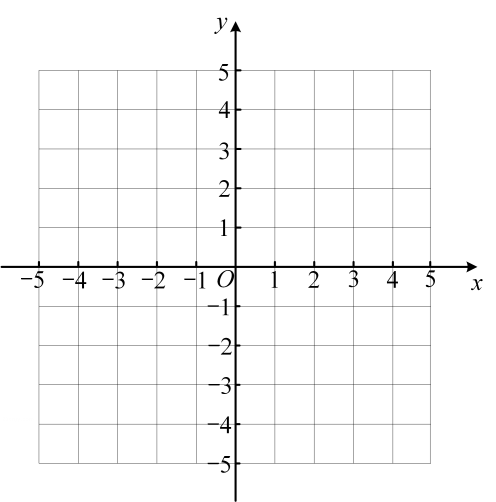下列问题：

(1)、请用描点法画出它的图象：
解：列表：
x 0 m
y 4 0
描点：以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点；
连线：把这两点连接起来，得到 $y = 2 x + 4$ 的图象；
表格中 $m$ 的值为；请在坐标系中画出 $y = 2 x + 4$ 的图象；

(2)、若一次函数 $y_{1} = k x + b$ 的图象与一次函数 $y = 2 x + 4$ 图象关于 $x$ 轴对称，请画出一次函数 $y_{1} = k x + b$ 的图象，并求出它的解析式；

(3)、若平行于 $y$ 轴的直线分别交 $y = 2 x + 4$ 的图象， $y_{1} = k x + b$ 的图象于 $A ， B$ 两点，已知 $A B$ 的长为4，则点 $A$ 的横坐标是.

查看试题解析
20. 某校为体育节的球类比赛筹备器材。他们从体育用品商店了解到，买2个篮球和4个足球需440元；买1个篮球和3个足球需285元。

(1)、求篮球和足球的单价各是多少；

(2)、该商店在周年庆期间有“每满300减30”的优惠活动，在此期间在该店一次性购买8个篮球和10个足球共需多少元？

查看试题解析
21. 【项目式学习】
【项目主题】合理规划，绿色家园
【项目背景】某小区有4栋住宅楼： $B$ 栋， $C$ 栋， $D$ 栋， $E$ 栋， $A$ 处为小区入口. 为方便小区居民传递爱心，物业管理处准备在小区的一条主干道 $B E$ 上增设一个“爱心衣物回收箱”（如图1），现需设计“爱心衣物回收箱”的具体位置，使得它到4栋住宅楼的距离之和最短。某数学兴趣小组成员开展了如下探究活动。
图11-1
任务一  实地测绘
小组成员借助无人机航测技术绘制了小区平面图（如图2），并测量出了某些道路的长度（如表格所示），进一步抽象成几何图形（如图3），其中主干道 $A C$ 与 $B E$ 交于点 $F$ ， $B E ∥ C D$ 。小组成员又借助电子角度仪测得 $∠ B C E = 9 0^{∘} ， ∠ C E B = ∠ C E D$ .
道路长度（米）
AE 40
AB 30
BC 30
BF 18
EF 32
DE 25
任务二  数学计算
根据图11-3及表格中的相关数据，请完成下列计算：

(1)、求道路 $C D$ 的长；

(2)、道路 $A C =$ 米；

(3)、任务三  方案设计
①根据以上探究，请你在主干道 $B E$ 上画出“爱心衣物回收箱”的具体位置（用点 $G$ 表示），并画出需要增设的小路 $C G ， D G$ ；
②“爱心衣物回收箱”到4栋住宅楼的距离之和的最小值为            米。（保留根号）

查看试题解析
22. 【定义】如图1，在同一平面内，点 $P ， Q$ 在线段 $M N$ 所在直线的两侧，若 $M P = N Q$ ，且 $∠ P M N = ∠ Q N M = 9 0^{∘}$ ，则称点 $P$ 与 $Q$ 是线段 $M N$ 的等垂对称点。

(1)、【理解】如图2，在正方形网格中，点 $A ， B ， C ， D ， E ， F$ 均在格点上，连接 $A B$ ，则下列各组点是线段 $A B$ 的等垂对称点的是；（填序号）
①点 $C$ 与点 $D$ ②点 $C$ 与点 $F$ ③点 $D$ 与点 $E$ ④点 $E$ 与点 $F$

(2)、如图3，在四边形 $A B C D$ 中， $E$ 是边 $B C$ 上一点，点 $B$ 与 $D$ 是线段 $A E$ 的等垂对称点，
①求证： $A D ∥ B C$ ；
②若 $D E$ 平分 $∠ A D C$ ，试探究 $∠ B C D$ 与 $∠ B$ 之间的数量关系，并说明理由。

(3)、【拓展】如图4，已知直线 $y = x + 4$ 与坐标轴交于点 $A ， B$ ，直线 $y = x - 2$ 与坐标轴交于点 $C ， D$ ，当点 $A ， B ， C ， D$ 中恰有两点是线段 $E F$ 的等垂对称点，且 $E F ∥ A B$ 时，请直接写出线段 $E F$ 的长。

查看试题解析

	平均数	众数	中位数
甲	1.69	a	1.68
乙	1.69	1.69	b

道路	长度（米）
AE	40
AB	30
BC	30
BF	18
EF	32
DE	25