广东省深圳重点大学附中2023-2024学年七年级(上)期末数学试卷
试卷更新日期:2024-03-07 类型:期末考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 的倒数是( )A、 B、 C、 D、2. 深圳市年的常住人口数量为万人,其中万用科学记数法可表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 在“世界无烟日”来临之际,小明和他的同学为了解某街道大约有多少成年人吸烟,于是随机调查了该街道个成年人,结果有个成年人吸烟.对于这个数据的收集与处理过程,下列说法正确的是( )A、调查的方式是普查 B、该街道约有的成年人吸烟 C、该街道只有个成年人不吸烟 D、样本是个吸烟的成年人5. 若与互余,且 , 则( )A、 B、 C、 D、6. 北京年月日的天气显示为如图,该天的温差是( )
 A、 B、 C、 D、7. 已知式子的值为 , 那么式子的值为( )A、 B、 C、 D、8. 孙子算经中记载:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何?大意为:今有头鹿进城,每家取一头鹿,没有取完,剩下的鹿每家共取一头,恰好取完,问:城中有多少户人家?设有户人家,可列方程为( )A、 B、 C、 D、9. 实数、、在数轴上对应点的位置如图所示,以下结论正确的是( )
A、 B、 C、 D、7. 已知式子的值为 , 那么式子的值为( )A、 B、 C、 D、8. 孙子算经中记载:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何?大意为:今有头鹿进城,每家取一头鹿,没有取完,剩下的鹿每家共取一头,恰好取完,问:城中有多少户人家?设有户人家,可列方程为( )A、 B、 C、 D、9. 实数、、在数轴上对应点的位置如图所示,以下结论正确的是( ) A、 B、 C、 D、10. 如图,把一个周长为定值的长方形分割为五个四边形,其中是正方形, , , , 都是长方形,这五个四边形的周长分别用 , , , , 表示,则下列各式的值为定值的是( )
A、 B、 C、 D、10. 如图,把一个周长为定值的长方形分割为五个四边形,其中是正方形, , , , 都是长方形,这五个四边形的周长分别用 , , , , 表示,则下列各式的值为定值的是( )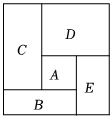 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共5小题,每小题3分,共15分。
-
11. 若 ,则x=12. 高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做蕴含的数学道理是。13. 如图表格是一张某月日历表,省去了号码数,设位置的数为 , 则位置的数可表示为 .
 14. 如图,点在直线上, , 若 , 则的大小为
14. 如图,点在直线上, , 若 , 则的大小为 15. 如图,商品条形码是商品的“身份证”,共有位数字.它是由前位数字和校验码构成,其结构分别代表“国家代码、厂商代码、产品代码、校验码”其中,校验码是用来校验商品条形码中前位数字代码的正确性.它的编制是按照特定的算法得来的.其算法为:
15. 如图,商品条形码是商品的“身份证”,共有位数字.它是由前位数字和校验码构成,其结构分别代表“国家代码、厂商代码、产品代码、校验码”其中,校验码是用来校验商品条形码中前位数字代码的正确性.它的编制是按照特定的算法得来的.其算法为:
步骤:计算前位数字中偶数位数字的和 , 即;
步骤:计算前位数字中奇数位数字的和 , 即;
步骤:计算与的和 , 即;
步骤:取大于或等于且为的整数倍的最小数 , 即;
步骤:计算与的差就是校验码 , 即 .
如图,若条形码中被污染的两个数字的和是 , 则被污染的两个数字中右边的数字是 .
三、解答题:本题共7小题,共55分。解答应写出文字说明,证明过程或演算步骤。
-
16. 计算:(1)、;(2)、;(3)、解方程: .17. 先化简,再求值: , 其中 , .18. 如图,是由个大小相同的小立方体块搭建的几何体,其中每个小正方体的棱长为厘米.
 (1)、请在指定位置画出该几何体从正面、左面和上面看到的形状图;(2)、在这个几何体上再添加一些相同的小正方体,使得从左面和上面看到的形状图不变,那么最多可以再添加个小正方体.19. 为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间单位:分钟 , 按照完成时间分成五组:“组:”“组:”“组:”“组:”组:”将收集的数据整理后,绘制成如图两幅不完整的统计图,根据以上信息,解答下列问题.
(1)、请在指定位置画出该几何体从正面、左面和上面看到的形状图;(2)、在这个几何体上再添加一些相同的小正方体,使得从左面和上面看到的形状图不变,那么最多可以再添加个小正方体.19. 为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间单位:分钟 , 按照完成时间分成五组:“组:”“组:”“组:”“组:”组:”将收集的数据整理后,绘制成如图两幅不完整的统计图,根据以上信息,解答下列问题. (1)、这次调查的样本容量是 , 请补全条形统计图;(2)、在扇形统计图中,组的圆心角是;(3)、若该校共有名学生,请你估计该校每天完成书面作业不超过分钟的学生人数.20. 现在,红旗商场进行促销活动,出售一种优惠购物卡注:此卡只作为购物优惠凭证不能顶替货款 , 花元买这种卡后,凭卡可在这家商场按标价的折购物.(1)、小张要买一台标价为元的冰箱,如何购买合算?小张能节省多少元钱?(2)、小张按合算的方案,把这台冰箱买下,如果红旗商场还能盈利 , 这台冰箱的进价是多少元?21. 如图 , 某校七年级数学学习小组在课后综合实践活动中,把一个直角三角尺的直角顶点放在互相垂直的两条直线、的垂足处,并使两条直角边落在直线、上,将绕着点顺时针旋转 .
(1)、这次调查的样本容量是 , 请补全条形统计图;(2)、在扇形统计图中,组的圆心角是;(3)、若该校共有名学生,请你估计该校每天完成书面作业不超过分钟的学生人数.20. 现在,红旗商场进行促销活动,出售一种优惠购物卡注:此卡只作为购物优惠凭证不能顶替货款 , 花元买这种卡后,凭卡可在这家商场按标价的折购物.(1)、小张要买一台标价为元的冰箱,如何购买合算?小张能节省多少元钱?(2)、小张按合算的方案,把这台冰箱买下,如果红旗商场还能盈利 , 这台冰箱的进价是多少元?21. 如图 , 某校七年级数学学习小组在课后综合实践活动中,把一个直角三角尺的直角顶点放在互相垂直的两条直线、的垂足处,并使两条直角边落在直线、上,将绕着点顺时针旋转 . (1)、如图 , 若 , 则 , ;(2)、若射线是的角平分线,且 .
(1)、如图 , 若 , 则 , ;(2)、若射线是的角平分线,且 .若旋转到图的位置,的度数为多少?用含的代数式表示
在旋转过程中,若 , 求此时的值.
22. 定义:如果两个一元一次方程的解之和为 , 我们就称这两个方程互为“阳光方程”例如:的解为 , 的解为 , 所以这两个方程互为“阳光方程”.(1)、若关于的一元一次方程与是“阳光方程”,则 .(2)、已知两个一元一次方程互为“阳光方程”,且这两个“阳光方程”的解的差为若其中一个方程的解为 , 求的值.(3)、已知关于的一元一次方程的解是 , 请写出解是的关于的一元一次方程:只需要补充含有的代数式 .若关于的一元一次方程和互为“阳光方程”,则关于的一元一次方程的解为 .