广西壮族自治区玉林市北流市2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个数中比 $- 4$ 小的数是（）

A、1 B、0 C、 $- 3$ D、 $- 5$

查看试题解析
2. 从三个不同方向看一个几何体，得到的平面图形如图所示，则这个几何体是（）

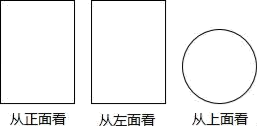A、圆柱 B、圆锥 C、棱锥 D、球

查看试题解析
3. 下列运用等式性质进行的变形中，正确的是（）

A、若 $a = b$ ，则 $a + 5 = b - 5$ B、若 $a = b$ ，则 $2 a = 3 b$ C、若 $a + b = 2 b$ ，则 $a = b$ D、若 $a = b + 2$ ，则 $2 a = 2 b + 2$

查看试题解析
4. 用四舍五入得到的近似数 $0.13$ 万精确到（）

A、十分位 B、百分位 C、百位 D、十位

查看试题解析
5. 若 $∠ α = 45 ° - n °$ ， $∠ β = 45 ° + n °$ ，则 $∠ α$ 与 $∠ β$ 的关系是（）

A、互补 B、互余 C、和为钝角 D、和为周角

查看试题解析
6. 如图，某同学用剪刀沿虚线将三角形剪掉一个角，发现四边形的周长比原三角形的周长要小，能正确解释这一现象的数学知识是（）

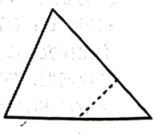A、两点之间，线段最短 B、经过一点，有无数条直线 C、垂线段最短 D、经过两点，有且只有一条直线

查看试题解析
7. 在解方程 $\frac{x}{3} = 1 - \frac{x - 1}{5}$ 时，去分母后正确的是（）

A、 $5 x = 15 - 3 (x - 1)$ B、 $x = 1 - (3 x - 1)$ C、 $5 x = 1 - 3 (x - 1)$ D、 $5 x = 3 - 3 (x - 1)$

查看试题解析
8. 下列说法正确的是（）

A、射线 $A B$ 和射线 $B A$ 不是同一条射线 B、若 $A O = B O$ ，则点 $O$ 是线段 $A B$ 的中点 C、 $10.15 ° = 10 ° 1 5^{'}$ D、晚上8点整，钟表的时针与分针的夹角是 $150 °$

查看试题解析
9. 如果 $- 3 x^{2} y > 0$ ，那么下列判断正确的是（）

A、 $x > 0 ， y > 0$ B、 $x < 0 ， y < 0$ C、 $x ， y$ 异号 D、 $x \neq 0 ， y < 0$

查看试题解析
10. 在排成每行七天的日历表中取下一个3×3的方块（如图），若方块中所有日期之和为207，则n的值为（　　）

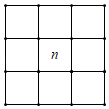A、23 B、21 C、15 D、12

查看试题解析
11. 如图所示，把一根绳子对折成线段 $A B$ ，然后从 $P$ 处将绳子剪断，如果 $A P$ 是 $P B$ 的一半，且剪断后的各段绳子中最长的一段为 $40 c m$ ，则绳子的原长为（）

A、 $80 c m$ B、 $100 c m$ C、 $60 c m$ 或 $120 c m$ D、 $120 c m$

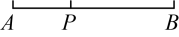查看试题解析
12. 正方形 $A B C D$ 在数轴上的位置如图所示，点 $A ， B$ 对应的数分别为 $- 1$ 和0，若正方形 $A B C D$ 绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点 $C$ 所对应的数为1；翻转2次后，点 $D$ 所对应的数为2；翻转3次后，点 $A$ 所对应的数为3；翻转4次后，点 $B$ 所对应的数为 $4 ， \cdot \cdot \cdot$ ，则连续翻转 $2024$ 次后，数轴上数 $2024$ 所对应的点是（）

A、 $A$ 点 B、 $B$ 点 C、 $C$ 点 D、 $D$ 点

查看试题解析

二、填空题

13. 写出一个解为 $x = - 2$ 的一元一次方程．

查看试题解析
14. 一个角的度数是 $28 ° 2 5^{'}$ ，则它的补角等于．

查看试题解析
15. 多项式 $3 x^{2} + 2 x y^{2} - 1$ 的次数是．

查看试题解析
16. 若 $m^{2} = 4 ， | n | = 1$ ，且 $m > n ， m - n =$ ．

查看试题解析
17. 《九章算术》是中国古代非常重要的一部数学典籍，被视为“算经之首”.《九章算术》大约成书于公元前200年~公元前50年，是以应用问题解法集成的体例编纂成书的，全书按题目的应用范围与解题方法划分为“方田”、“粟米”、“衰分”等九章.
《九章算术》中有这样一个问题：

今有共买金，人出四百，盈三千四百；人出三百，盈一百.问人数，金价各几何？

其大意是：假设合伙买金，每人出400钱，还剩余3400钱；每人出300钱，还剩余100钱.问人数、金价各是多少？如果设有x个人，那么可以列方程为

查看试题解析
18. 如图，点 $O$ 是量角器的中心点，射线 $O M$ 经过刻度线 $90$ ．若 $∠ A O B = ∠ C O D$ ．射线 $O A$ 、 $O B$ 分别经过刻度线 $40$ 和 $60$ ， $∠ C O D$ 在刻度线 $O M$ 的右侧．下列结论：① $∠ A O C = ∠ B O D$ ；②若 $∠ A O C$ 与 $∠ B O C$ 互补，则射线 $O D$ 经过刻度线 $165$ ；③若 $∠ M O C = 3 ∠ C O D$ ，则图中共有6对角互为余角．其中正确的是（填序号）．

查看试题解析

三、解答题

19.

(1)、 ${(- 1)}^{2024} - (- 9) - | - 1 |$ ；

(2)、解方程： $3 (x + 2) - 1 = x - 3$

查看试题解析
20. 如图，已知同一平面内的线段 $A B$ 及点 $C$ ．

(1)、画直线 $A C$ ，线段 $B C$ ；

(2)、用圆规在线段 $A B$ 的延长线上截取 $B D = B C$ （保留画图痕迹）；

(3)、连接 $C D$ ，并画出 $C D$ 的反向延长线．

查看试题解析
21. 先化简，再求值： $- 2 (3 x - 2 x^{2} y) + 3 (2 x - x^{2} y + x y)$ ，其中 $x$ 是最大的负整数， $y$ 的相反数是2．

查看试题解析
22. 综合与实践
问题情境：
在数学活动课上，老师让同学们制作了一些边长为 $20 c m$ 的正方形纸片，并要求各个小组利用这些纸片研究数学问题．
实践操作：

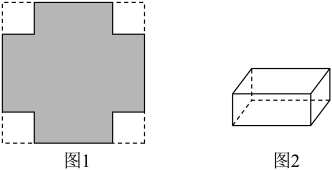(1)、勤勉小组提出：将如图1所示的纸片的四个角各剪去一个相同的正方形，得到图1中的阴影部分，若剪去的小正方形的边长为 $x c m$ ，请计算阴影部分的面积S（用含 $x$ 的式子表示），并求出当 $x = 3$ 时，阴影部分的面积；

(2)、创新小组将图1中的阴影部分折成一个无盖的长方体盒子，如图2，请求出折成的长方体盒子的容积V（用含 $x$ 的式子表示），并求出当 $x = 3$ 时，折成的长方体盒子的容积．

查看试题解析
23. 我们定义：对于数对 $(a ， b)$ ，若 $a + b = a b$ ，则 $(a ， b)$ 称为“和积等数对”．如：因为 $2 + 2 = 2 \times 2$ ， $- 3 + \frac{3}{4} = - 3 \times \frac{3}{4}$ ，所以 $(2 ， 2)$ ， $(- 3 ， \frac{3}{4})$ 都是“和积等数对”．

(1)、下列数对中，是“和积等数对”的是；（填序号）
① $(3 ， 1.5)$ ；② $(\frac{3}{4} ， 1)$ ；③ $(- \frac{1}{2} ， \frac{1}{3})$ ．

(2)、若 $(- 5 ， x)$ 是“和积等数对”，求x的值；

(3)、若 $(m ， n)$ 是“和积等数对”，求代数式 $4 [m n + m - 2 (m n - 3)] - 2 (3 m^{2} - 2 n) + 6 m^{2}$ 的值．

查看试题解析

24. 数学课上，黎老师提出问题：如图，点

O

是线段

A B

上一点，

C ， D

分别是线段

A O ， B O

的中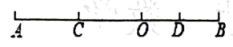点，当

A B = 10

时，求线段

C D

的长度．

(1)、下面是小漾同学根据黎老师的要求进行的分析及解答过程，请你补全解答过程的填空；

思路方法

解答过程

知识要素

未知线段

$\overset{转化}{\to}$

已知线段

$⋅ ⋅ ⋅$

因为 $C ， D$ 分别是线段 $A O ， B O$ 的中点，所以 $C O = \frac{1}{2} A O ， D O = \frac{1}{2}$ ．因为 $A B = 10$ ，所以

$C D = C O + D O = \frac{1}{2} A O + \frac{1}{2}$

$= \frac{1}{2}$ $=$ ．

线段中点的定义线段的和、差等式的性质 $⋅ ⋅ ⋅$

(2)、小漾同学进行题后反思，提出新的问题：如果点

O

运动到线段

A B

的延长线上，

C D

的长度是否会发生变化？请你帮助小漾同学作出判断并说明理由．

查看试题解析

25. 大润发和通用两家超市相同商品的标价相同，在2024新年即将到来之际，两大超市分别推出如下促销活动：
大润发超市：全场均按八五折优惠；
通用超市：购物不超过200元，不给予优惠；超过了200元而不超过500元一律打八八折；超过500元时，其中的500元优惠 $12 %$ ，超过500元的部分打八折；

(1)、当购物总额是多少时，大润发、通用两家超市实际付款相同？

(2)、某顾客在通用超市购物实际付款490元，试问该顾客的选择划算吗？试说明理由．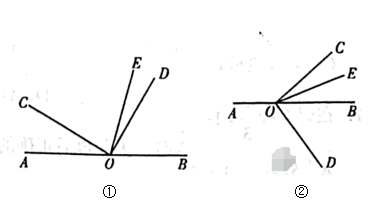

查看试题解析
26. 已知 $O$ 是直线 $A B$ 上的一点， $∠ C O D$ 是直角， $O E$ 平分 $∠ B O C$ ．

(1)、初步尝试：如图①，若 $∠ A O C = 30 °$ ．求 $∠ D O E$ 的度数；

(2)、类比探究：在图①中，若 $∠ A O C = α$ ，求 $∠ D O E$ 的度数（用含 $α$ 的式子表示）；

(3)、解决问题：如图②， $O$ 是直线 $A B$ 上的一点， $∠ C O D$ 是直角， $O E$ 平分 $∠ B O C$ ，探究 $∠ A O C$ 和 $∠ D O E$ 的度数之间的数量关系．

查看试题解析