广东省汕头市潮阳区2023-2024学年高一上学期1月期末教学质量监测数学试题

试卷更新日期：2024-03-07 类型：月考试卷

进入出卷网下载

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. $t a n (- 300 °) =$ （）

A、 $\sqrt{3}$ B、1 C、 $\frac{\sqrt{3}}{3}$ D、 $- \frac{\sqrt{3}}{3}$

查看试题解析
2. 已知集合 $A = {x | 2 x - 1 < 0}$ ， $B = {x | 0 \leq x \leq 1}$ ，那么 $A \cap B$ 等于（）

A、 ${x | x \geq 0}$ B、 ${x | x \leq 1}$ C、 ${x | 0 < x < \frac{1}{2}}$ D、 ${x | 0 \leq x < \frac{1}{2}}$

查看试题解析
3. 下列函数是偶函数的是（）

A、 $y = c o s (x - 1)$ B、 $y = | 2^{x} - 1 |$ C、 $y = {(x - 1)}^{2}$ D、 $y = l o g_{2} (x^{2} - 1)$

查看试题解析
4. 若 $x > 0$ ，则 $x + \frac{4}{x} - 2$ 的最小值为（）

A、 $- 2$ B、0 C、2 D、3

查看试题解析
5. 下列命题正确的是（）

A、 $y = c o s x$ 在 $(- \frac{π}{2} ， \frac{π}{2})$ 是减函数 B、正切函数 $y = t a n x$ 在定义域内是增函数 C、 $y = | s i n x |$ 是偶函数也是周期函数 D、已知 $y = k s i n x + 1$ ， $x \in R$ ，则y的最小值为 $- k + 1$

查看试题解析
6. 人工放射性核素碘-131可发射 $β$ 射线治疗甲亢，已知该物质的半衰期为8天，设质量为a的碘-131经过x天后剩留的质量为y ，则y关于x的函数解析式是（）

A、 $y = a {(\frac{1}{2})}^{\frac{x}{8}}$ ， $x \in N^{*}$
B、 $y = a {(\frac{1}{2})}^{8 x}$ ， $x \in N^{*}$ C、 $y = a {(\frac{0.5}{8})}^{x}$ ， $x \in N^{*}$ D、 $y = a {(0.5)}^{\frac{x}{4}}$ ， $x \in N^{*}$

查看试题解析
7. 已知 $p ： m > n > 0$ ， $q ： \frac{n + 1}{m + 1} > \frac{n}{m}$ ，则p是q的（）

A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件

查看试题解析
8. 已知函数 $f (x) = {\begin{cases} x + 1 ， x > 0 \\ f (f (x + 1)) ， x \leq 0 \end{cases}$ ；则 $f (- 2) =$ （）

A、2 B、3 C、4 D、5

查看试题解析

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，至少有两项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 如图所示的是某池塘中的浮萍蔓延的面积y（ $m^{2}$ ）与时间t（月）的关系为 $y = a^{t}$ ，则以下叙述正确的有（）

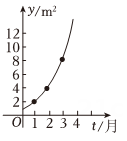A、浮萍蔓延的面积逐月翻一番 B、第5个月时，浮萍面积会超过30 $m^{2}$ C、第7个月的浮萍面积超过第6个月和第8个月的平均值 D、浮萍每月增加的面积都相等

查看试题解析
10. 若 $m \geq 1$ ，则（）

A、 $1 - m \leq 0$ B、 $m^{3} \geq 1$ C、 $m^{2} \leq m$ D、 ${(\frac{2}{3})}^{m} > {(\frac{1}{3})}^{m}$

查看试题解析
11. 下列求解结果正确的是（）

A、不等式 $(x - 1) \sqrt{x + 2} \geq 0$ 的解集为 $[1 ， + \infty)$ B、 $2 {(l g 2)}^{2} + l g 5 l g 20 + l g 2 l g 50 + l g 25 = 6$ C、 $\sqrt[6]{24} \times \sqrt[3]{3} \times \sqrt{\frac{3}{2}} = 3$ D、若 $\frac{s i n α}{c o s α - 1} = - \frac{1}{2}$ ，则 $\frac{1 + c o s α}{s i n α} = \frac{1}{2}$

查看试题解析
12. 已知函数 $y = f (x)$ 的图象关于 $P (a ， b)$ 成中心对称图形的充要条件是 $y = f (x + a) - b$ 是奇函数，函数 $y = f (x)$ 的图象关于 $x = a$ 成轴对称图形的充要条件是 $y = f (x + a)$ 是偶函数．则下列说法正确的是（）

A、 $f (x) = x^{3} - 3 x^{2}$ 的图象关于点 $(1 ， - 2)$ 成中心对称图形 B、 $f (x) = x^{4} - 4 x^{3} + 6 x^{2} - 4 x$ 的图象关于 $x = 1$ 成轴对称图形 C、 $f (x) = \frac{2 x + 1}{x - 1}$ 的图象关于点 $(1 ， - 2)$ 成中心对称图形 D、 $f (x) = \frac{x - 2}{x^{2} - 4 x + 5}$ 的图象关于点 $(- 2 ， 0)$ 成中心对称图形

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分．

13. 命题p：“ $\exists x \in R$ ， $e^{x} - x - 1 \leq 0$ ”则命题p的否定为：．

查看试题解析
14. 已知函数 $f (x) = 2^{x}$ 的值域是 $[2 ， 4]$ ，记 $φ (x) = f (x) + l o g_{2} (x - \frac{3}{2})$ 的定义域为：．

查看试题解析
15. 记 $A = 1 \times 2 \times 3 \times \cdot \cdot \cdot \times 2024$ ，那么 $\frac{1}{l o g_{2} A} + \frac{1}{l o g_{3} A} + \frac{1}{l o g_{4} A} + \cdot \cdot \cdot + \frac{1}{l o g_{2024} A} =$ ．

查看试题解析
16. 已知函数 $f (x) = \frac{e^{x} - 1}{e^{x} + 1}$ ，若对任意的正数a、b ，满足 $f (a) + f (2 b - 2) = 0$ ，则 $\frac{2}{a} + \frac{1}{b}$ 的最小值为：．

查看试题解析

四、解答题：本题共6小题，第17题满分10分，其它5个小题满分均为12分，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 在平面直角坐标系 $x O y$ 中，角 $α$ 以 $O x$ 为始边，它的终边与单位圆交于第二象限内的点 $P (x ， y)$ ．

(1)、若 $y = \frac{2 \sqrt{5}}{5}$ ，求 $t a n α$ 及 $\frac{7 s i n α + 2 c o s α}{s i n α - 4 c o s α}$ 的值；

(2)、若 $\frac{s i n α}{1 - c o s α} = \frac{1}{2}$ ，求点P的坐标．

查看试题解析
18. 已知函数 $f (x) = \sqrt{x}$ ； $g (x) = f (l o g_{\frac{1}{2}} (9 - x^{2}))$

(1)、判断函数 $f (x)$ 在区间 $[0 ， + \infty)$ 上的单调性，并用定义证明；

(2)、求不等式 $g (x) \leq 1$ 的解集．

查看试题解析
19. 潮汕人喜欢喝功夫茶，茶水的口感和水的温度有关，如果刚泡好的茶水温度是 $θ_{1}$ ℃，环境温度是 $θ_{0}$ ℃，那么t分钟后茶水的温度 $θ$ （单位：℃）可由公式 $θ (t) = θ_{0} + (θ_{1} - θ_{0}) e^{- k t}$ 求得．现有刚泡好茶水温度是100℃，放在室温25℃的环境中自然冷却，5分钟以后茶水的温度是50℃．

(1)、求k的值；

(2)、经验表明，当室温为15℃时，该种茶刚泡好的茶水温度95℃，自然冷却至60℃时饮用，可以产生最佳口感，那么，刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感？（结果精确到0.1；参考值： $l n 2 \approx 0.7$ ， $l n 3 \approx 1.1$ ）

查看试题解析
20. 已知函数 $f (x) = l o g_{3} (9^{x} + 1) - a x$ 是偶函数．

(1)、求实数a的值；

(2)、当 $x \geq 0$ 时，函数 $g (x) = 3^{x} + 3^{f (x)} - t$ 有零点，求实数t的取值范围．

查看试题解析
21. 已知二次函数 $f (x)$ 满足 $\forall x \in R$ ， $f (x - 2) = f (- x)$ 恒成立；且 $f (0) = 4$ ， $f (- 1) = 3$ ．

(1)、求 $f (x)$ 的解析式；

(2)、对任意 $λ \in R$ ，总存在 $μ \in [- 4 ， 4]$ ，使得不等式 $| f (μ) - μ^{2} + λ | \geq k$ 成立，求实数k的取值范围．

查看试题解析
22. 定义：函数 $f (x)$ 若存在正常数T ，使得 $f (x + T) = f (x) + M$ ， M为常数，对任意 $x \in R$ 恒成；则称函数 $f (x)$ 为“T代M阶函数”．

(1)、判断下列函数是否为“2代M阶函数”？并说明理由．
① $f_{1} (x) = s i n π x$ ， ② $f_{2} (x) = 2^{x}$ ．

(2)、设函数 $F (x) = f (x) + g (x)$ 为“4代M阶函数”，其中 $f (x)$ 是奇函数， $g (x)$ 是偶函数．若 $f (2) = 1$ ，求 $f (2026)$ 的值．

查看试题解析