广东省汕头市潮阳区2023-2024学年高二上学期1月期末教学质量监测数学试题

试卷更新日期：2024-03-07 类型：期末考试

进入出卷网下载

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 拼音chao所有字母组成的集合记为 $A$ ，拼音yang所有字母组成的集合记为 $B$ ，则 $A ∩ B =$ （）

A、 ${c}$ B、 ${h}$ C、 ${a}$ D、 ${0}$

查看试题解析
2. 设 $z = \frac{1 + i}{i^{3}}$ ，则 $| z | =$ （）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
3. 已知 $A$ 为抛物线 $C$ ： $y^{2} = 2 p x$ （ $p > 0$ ）上一点，点 $A$ 到 $C$ 的焦点的距离为8，到 $y$ 轴的距离为5，则 $p =$ （）

A、2 B、3 C、6 D、9

查看试题解析
4. 已知函数 $f (x) = {(\frac{1}{3})}^{x} - l o g_{2} x$ ，若实数 $x_{0}$ 是函数 $f (x)$ 的零点，且 $0 < x_{1} < x_{0}$ ，则 $f (x_{1})$ 的值（）

A、恒为正 B、等于0 C、恒为负 D、不大于0

查看试题解析
5. 设 $a = \frac{2 t a n 25 °}{1 - t a n^{2} 25 °}$ ， $b = 2 s i n 25 ° c o s 25 °$ ， $c = \sqrt{\frac{1 + c o s 100 °}{2}}$ ，则有（）

A、 $b < c < a$ B、 $a < b < c$ C、 $a < c < b$ D、 $c < b < a$

查看试题解析
6. 若等差数列 ${a_{n}}$ 的前项和为 $S_{n}$ ，且 $a_{1} > 0$ ， $a_{3} + a_{10} > 0$ ， $a_{6} a_{7} < 0$ ，则满足 $S_{n} > 0$ 的最大自然数 $n$ 的值为（）

A、6 B、7 C、12 D、13

查看试题解析
7. 已知函数 $f (x) = l n x + l n (2 - x)$ ，则（）

A、 $f (x)$ 在 $(0 ， 2)$ 单调递增 B、 $f (x)$ 在 $(0 ， 2)$ 单调递减 C、 $y = f (x)$ 的图像关于点 $(1 ， 0)$ 对称 D、 $y = f (x)$ 的图像关于直线 $x = 1$ 对称

查看试题解析
8. 如图，在一个单位正方形中，首先将它等分成4个边长为 $\frac{1}{2}$ 的小正方形，保留一组不相邻的2个小正方形，记这2个小正方形的面积之和为 $S_{1}$ ；然后将剩余的2个小正方形分别继续四等分，各自保留一组不相邻的2个小正方形，记这4个小正方形的面积之和为 $S_{2}$ ．以此类推，操作 $n$ 次，若 $S_{1} + S_{2} + \cdot \cdot \cdot + S_{n} \geq \frac{2023}{2024}$ ，则 $n$ 的最小值是（）

A、12 B、11 C、10 D、9

查看试题解析

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，至少有两项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 若直线 $y = \sqrt{3} x + b$ 与圆 $x^{2} + y^{2} = 1$ 相切，则 $b$ 的取值可以是（）

A、 $- 2$ B、 $\sqrt{2}$ C、2 D、 $\sqrt{5}$

查看试题解析
10. 已知一组样本数据 $x_{1}$ ， $x_{2}$ ， …， $x_{15}$ ，其中 $x_{i} = 2 i$ （ $i = 1 ， 2 ， \cdot \cdot \cdot ， 15$ ），由这组数据得到另一组新的样本数据 $y_{1}$ ， $y_{2}$ ， …， $y_{15}$ ，其中 $y_{i} = x_{i} - 20$ ，则（）

A、两组样本数据的样本方差相同 B、两组样本数据的样本平均数相同 C、 $y_{1}$ ， $y_{2}$ ， …， $y_{15}$ 样本数据的第30百分位数为 $- 10$ D、将两组数据合成一个样本容量为30的新的样本数据，该样本数据的平均数为5

查看试题解析
11. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，已知 $A B = 4$ ， $B C = A A_{1} = 2$ ，点 $P$ 在线段 $A D_{1}$ 上运动（不含端点），则下列说法正确的是（）

A、 $B P \in [4 ， 2 \sqrt{6}]$ B、三棱锥 $B_{1} - A_{1} B C_{1}$ 的体积为 $\frac{8}{3}$ C、平面 $C_{1} D_{1} P ⊥$ 平面 $B_{1} C P$ D、若点 $P$ 是线段 $A D_{1}$ 的中点，则三棱锥 $P - A B D$ 的外接球的表面积为 $20 π$

查看试题解析
12. 设 $F_{1}$ ， $F_{2}$ 为椭圆 $C$ ： $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ 的两个焦点， $P (x_{0} ， y_{0})$ 为 $C$ 上一点且在第一象限， $I (x_{1} ， y_{1})$ 为 $△ F_{1} P F_{2}$ 的内心，且 $△ F_{1} P F_{2}$ 内切圆半径为1，则（）

A、 $| I P | = 2$ B、 $y_{0} = \frac{8}{3}$ C、 $| O I | = \sqrt{6}$ D、 $O$ 、 $I$ 、 $P$ 三点共线

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分．

13. 将函数 $y = s i n x$ 的图象纵坐标不变，横坐标扩大为原来的3倍，则得到了函数为．

查看试题解析
14. 已知数列 ${a_{n}}$ 为等比数列， $a_{1} = 1$ ， $a_{5} = 16$ ，则 $a_{3} =$ ．

查看试题解析
15. 如图，正方形 $A B C D$ 中， $\vec{D E} = 2 \vec{E C}$ ， $P$ 是线段 $B E$ 上的动点且 $\vec{A P} = x \vec{A B} + y \vec{A D}$ （ $x > 0$ ， $y > 0$ ），则 $\frac{3}{x} + \frac{1}{y}$ 的最小值为．

查看试题解析
16. 定义：点 $P$ 为曲线 $L$ 外的一点， $A$ ， $B$ 为 $L$ 上的两个动点，则 $∠ A P B$ 取最大值时， $∠ A P B$ 叫点 $P$ 对曲线 $L$ 的张角．已知点 $P$ 为双曲线 $C$ ： $x^{2} - \frac{y^{2}}{8} = 1$ 上的动点，设 $P$ 对圆 $M$ ： ${(x - 3)}^{2} + y^{2} = 1$ 的张角为 $θ$ ，则 $c o s θ$ 的最小值为．

查看试题解析

四、解答题：本题共6小题，第17题满分10分，其它5个小题满分均为12分，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 已知 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别是 $a ， b ， c$ ，且 $b \sin 2 A = a \sin B$ .

(1)、求A；

(2)、若 $a = 2$ ， $△ A B C$ 的面积为 $\sqrt{3}$ ，求 $△ A B C$ 的周长.

查看试题解析
18. 2023年上海书展于8月16日至22日在上海展览中心举办.展会上随机抽取了50名观众，调查他们每个月用在阅读上的时长，得到如图所示的频率分布直方图：

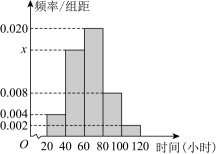(1)、求x的值，并估计这50名观众每个月阅读时长的平均数；

(2)、用分层抽样的方法从 $[20 ， 40) ， [80 ， 100)$ 这两组观众中随机抽取6名观众，再若从这6名观众中随机抽取2人参加抽奖活动，求所抽取的2人恰好都在 $[80 ， 100)$ 这组的概率.

查看试题解析
19. 已知正项数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ ，满足： $S_{n} = {(\frac{a_{n} + 1}{2})}^{2}$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、记 $b_{n} = \frac{1}{\sqrt{S_{n}} \sqrt{S_{n + 1}}}$ ，设数列 ${b_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，求 $T_{n}$ ．

查看试题解析
20. 如图，已知长方体 $A C_{1}$ 中， $A B = B C = 1$ ， $B B_{1} = 2$ ，连接 $B_{1} C$ ，过 $B$ 点作 $B_{1} C$ 的垂线交 $C C_{1}$ 于 $E$ ，交 $B_{1} C$ 于 $F$ ．

(1)、求证： $A_{1} C ⊥$ 平面 $E B D$ ；

(2)、求点 $A$ 到平面 $A_{1} B_{1} C$ 的距离；

(3)、求直线 $D E$ 与平面 $A_{1} B_{1} C$ 所成角的正弦值．

查看试题解析
21. 随着科技的发展，手机上各种APP层出不穷，其中抖音就是一种很火爆的自媒体软件，抖音是一个帮助用户表达自我，记录美好生活的视频平台．在大部分人用来娱乐的同时，部分有商业头脑的人用抖音来直播带货，可谓赚得盆满钵满，抖音上商品的价格随着播放的热度而变化．经测算某服装的价格近似满足： $J = J_{b} + (J_{0} - J_{b}) {(\frac{1}{2})}^{\frac{1}{h}}$ ，其中 $J_{0}$ （单位：元）表示开始卖时的服装价格， $J$ （单位：元）表示经过一定时间 $t$ （单位：天）后的价格， $J_{b}$ （单位：元）表示波动价格， $h$ （单位：天）表示波动周期．某位商人通过抖音卖此服装，开始卖时的价格为每件120元，波动价格为每件20元，服装价格降到70元每件时需要10天时间．

(1)、求 $h$ 的值；

(2)、求服装价格降到60元每件时需要的天数．（结果精确到整数）
参考数据： $l g 2 \approx 0.3010$

查看试题解析
22. 已知 $F_{1} ， F_{2}$ 分别为椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点，椭圆E的离心率为 $\frac{1}{2}$ ，过 $F_{2}$ 且不与坐标轴垂直的直线 $l$ 与椭圆E交于A，B两点， $△ F_{1} A B$ 的周长为8．

(1)、求椭圆E的标准方程；

(2)、过 $F_{1}$ 且与 $l$ 垂直的直线 $l^{'}$ 与椭圆E交于C，D两点，求四边形ACBD面积的最小值．

查看试题解析