广东省广州市重点中学2023-2024学年高三上学期第一次调研数学试题
试卷更新日期:2024-03-07 类型:高考模拟
一、单选题(本大题8小题,每小题5分,共40分)
-
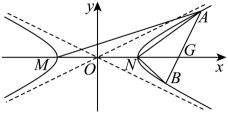
1. 已知集合 , , 则( )A、 B、或 C、或 D、2. 是虚数单位,复数满足 , 则( )A、 B、 C、 D、3. 已知两单位向量与的夹角为 , 则向量与的夹角( )A、 B、 C、 D、4. 在锐角中,若 , 则的取值范围是( )A、 B、 C、 D、5. 数列成为斐波那契数列,是由十三世纪意大利数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,该数列从第三项开始,每项等于其前两相邻两项之和,记该数的前项和为 , 则下列结论正确的是( )A、 B、 C、 D、6. 生物学家认为,睡眠中的恒温动物的脉搏率(单位:心跳次数)与体重(单位:)的次方成反比.若、为两个睡眠中的恒温动物,的体重为、脉搏率为210次 , 的脉搏率是70次 , 则的体重为( )A、 B、 C、 D、7. 已知正三棱锥的底面边长为 , 外接球表面积为 , , 点M , N分别是线段AB , AC的中点,点P , Q分别是线段SN和平面SCM上的动点,则的最小值为( )A、 B、 C、 D、8. 点均在抛物线上,若直线分别经过两定点 , 则经过定点 , 直线分别交轴于 , 为原点,记 , 则的最小值为( )A、 B、 C、 D、
二、多选题(本大题共4小题,每小题5分,共20分.每题在给出的四个选项中,有多项符合要求,全部选对得5分,选对但不全的得2分,有选错的得0分)
-
9. 将函数的图象向右平移个单位长度,再把所得图象上各点的横坐标缩短为原来的 , 纵坐标保持不变,得到函数的图象,则关于的说法正确的是( )A、最小正周期为 B、偶函数 C、在上单调递减 D、关于中心对称10. 如图,在平面直角坐标系中,直角三角形中, , 它的两个锐角的顶点A和B分别在x正半轴、y正半轴上滑动,则下列结论正确的是( )
 A、点C在直线 上 B、点C在直线上 C、点C的轨迹长度等于 D、点C的轨迹长度等于11. 投掷一枚质地不均匀的硬币,已知出现正面向上的概率为p , 记表示事件“在n次投掷中,硬币正面向上出现偶数次”,则下列结论正确的是( )A、与是互斥事件 B、 C、 D、12. 设函数 , 则( )A、 B、函数有最大值 C、若 , 则 D、若 , 且 , 则
A、点C在直线 上 B、点C在直线上 C、点C的轨迹长度等于 D、点C的轨迹长度等于11. 投掷一枚质地不均匀的硬币,已知出现正面向上的概率为p , 记表示事件“在n次投掷中,硬币正面向上出现偶数次”,则下列结论正确的是( )A、与是互斥事件 B、 C、 D、12. 设函数 , 则( )A、 B、函数有最大值 C、若 , 则 D、若 , 且 , 则三、填空题(本大题4小题,每小题5分,共20分)
-
13. 在的二项式中,所有的二项式系数之和为256,则常数项等于 .14. 已知数列中, , 为数列的前项和,且 , 则.15. 已知 , 分别是椭圆的左、右焦点,P点是直线上一动点,当P点的纵坐标为时,最大,则椭圆C的离心率为 .16. 函数的定义域为 , 其导函数为 , 若 , 且当时, , 则不等式的解集为 .
四、解答题(本大题6小题,共70分)
-
17. 在中,角 , , 对的边分别为 , , , , .(1)、求的值;(2)、若 , 求的面积.18. 已知数列是等差数列, , 的前项和为 , 满足 , 是数列的前项和,且 , , 成等比数列.(1)、求数列和的通项公式;(2)、求数列前项的和 .19. 如图,平行四边形中, , 将沿翻折,得到四面体 .
 (1)、若 , 作出二面角的平面角,说明作图理由并求其大小;(2)、若 , 求点到平面的距离.20. 某电商专门生产某种电子元件,生产的电子元件除编号外,其余外观完全相同,为了检测元件是否合格,质检员设计了图甲、乙两种电路.
(1)、若 , 作出二面角的平面角,说明作图理由并求其大小;(2)、若 , 求点到平面的距离.20. 某电商专门生产某种电子元件,生产的电子元件除编号外,其余外观完全相同,为了检测元件是否合格,质检员设计了图甲、乙两种电路. (1)、在设备调试初期,已知该电商试生产了一批电子元件共5个,只有2个合格,质检员从这批元件中随机抽取2个安装在甲图电路中的 , 处,请用集合的形式写出试验的样本空间,并求小灯泡发亮的概率;(2)、通过设备调试和技术升级后,已知该电商生产的电子元件合格率为0.9,且在生产过程中每个电子元件是否合格互不影响,质检员从该电商生产的一批电子元件中随机抽取3个安装在乙图电路中的 , , 处,求小灯泡发亮的概率.
(1)、在设备调试初期,已知该电商试生产了一批电子元件共5个,只有2个合格,质检员从这批元件中随机抽取2个安装在甲图电路中的 , 处,请用集合的形式写出试验的样本空间,并求小灯泡发亮的概率;(2)、通过设备调试和技术升级后,已知该电商生产的电子元件合格率为0.9,且在生产过程中每个电子元件是否合格互不影响,质检员从该电商生产的一批电子元件中随机抽取3个安装在乙图电路中的 , , 处,求小灯泡发亮的概率.