贵州省桐梓县荣兴高级中学2023-2024学年高二上学期第四次月考数学试卷
试卷更新日期:2024-03-07 类型:月考试卷
一、单选题
-
1. 若 , 则( )A、 B、 C、 D、2. 直线的倾斜角为( )A、 B、 C、 D、3. 函数的图象大致是( )A、
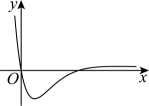 B、
B、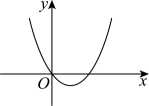 C、
C、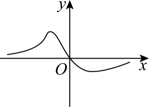 D、
D、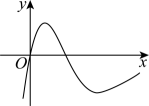 4. 已知抛物线上的点到其焦点的距离为4,则( )A、1 B、2 C、3 D、45. 已知偶函数的定义域为R,当时, , 则的大小关系是( )A、 B、 C、 D、6. “”是“直线和直线平行”的( )A、充要条件 B、必要不充分条件 C、充分不必要条件 D、既不充分也不必要条件7. 两条不同直线的方向向量分别为 , 则这两条直线( )A、平行 B、垂直 C、异面 D、相交或异面8. 抛掷一枚质地均匀的骰子两次,设“第一次向上的点数是2”为事件 , “第二次向上的点数是奇数”为事件 , “两次向上的点数之和能被3整除”为事件 , 则下列说法正确的是( )A、事件与事件互为对立事件 B、 C、 D、事件与事件相互不独立
4. 已知抛物线上的点到其焦点的距离为4,则( )A、1 B、2 C、3 D、45. 已知偶函数的定义域为R,当时, , 则的大小关系是( )A、 B、 C、 D、6. “”是“直线和直线平行”的( )A、充要条件 B、必要不充分条件 C、充分不必要条件 D、既不充分也不必要条件7. 两条不同直线的方向向量分别为 , 则这两条直线( )A、平行 B、垂直 C、异面 D、相交或异面8. 抛掷一枚质地均匀的骰子两次,设“第一次向上的点数是2”为事件 , “第二次向上的点数是奇数”为事件 , “两次向上的点数之和能被3整除”为事件 , 则下列说法正确的是( )A、事件与事件互为对立事件 B、 C、 D、事件与事件相互不独立二、多选题
-
9. 设函数 , 则下列结论错误的是( )A、的最小正周期为 B、的图象关于直线对称 C、的一个零点为 D、的最大值为110. 已知圆C: , 直线l:(),下列说法正确的是( )A、无论a取何值,直线l与圆C相交 B、直线l被圆C截得的最短弦长为4 C、若 , 则圆C关于直线l对称的圆的方程为 D、直线l的方程能表示过点的所有直线的方程11. 已知 , 分别是双曲线:的左、右焦点,点是双曲线上异于双曲线顶点的一点,且 , 则下列结论正确的是( )A、双曲线C的离心率为 B、的面积为 C、到双曲线的一条渐近线的距离为 D、以为直径的圆的方程为12. 对于抛物线 , 下列描述不正确的是( )A、开口向上,焦点为 B、开口向上,焦点为 C、准线方程为 D、准线方程为
三、填空题
-
13. 已知点 , 若 , , 则点坐标为.14. 若角 的终边经过点 ,则 .15. 已知实数 , 函数 , 若 , 则a的值为.16. 下列四个幂函数:①;②;③;④的值域为同一区间的是.(只需填写正确答案的序号)
四、问答题
-
17. 某中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲、乙两位同学的20次成绩如茎叶图所示:

 (1)、根据茎叶图求甲、乙两位同学成绩的中位数,并将乙同学的成绩的频率分布直方图填充完整;(2)、根据茎叶图比较甲、乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可).18. 在中,内角所对的边分别为 , , , 已知已知.(1)、求角的大小;(2)、若 , , 求的值;(3)、若 , 判断的形状.19. 圆的圆心坐标为 , 且过点(1)、求圆的方程;(2)、判断直线与圆的位置关系,说明理由.如果相交,则求弦长.
(1)、根据茎叶图求甲、乙两位同学成绩的中位数,并将乙同学的成绩的频率分布直方图填充完整;(2)、根据茎叶图比较甲、乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可).18. 在中,内角所对的边分别为 , , , 已知已知.(1)、求角的大小;(2)、若 , , 求的值;(3)、若 , 判断的形状.19. 圆的圆心坐标为 , 且过点(1)、求圆的方程;(2)、判断直线与圆的位置关系,说明理由.如果相交,则求弦长.