广东省揭阳市普宁市2023-2024学年高二上学期期末数学试题
试卷更新日期:2024-03-07 类型:期末考试
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合要求.
-
1. 已知椭圆 , 则它的短轴长为( )A、2 B、4 C、6 D、82. 已知直线m经过 , 两点,则直线m的斜率为( )A、-2 B、 C、 D、23. 已知空间向量 , , 则( )A、 B、19 C、17 D、4. 在等差数列中,已知 , 则数列的前6项之和为( )A、12 B、32 C、36 D、375. 地震预警是指在破坏性地震发生以后,在某些区域可以利用“电磁波”抢在“地震波”之前发出避险警报信息,以减小相关预警区域的灾害损失.根据Rydelek和Pujol提出的双台子台阵方法,在一次地震发生后,通过两个地震台站的位置和其接收到的信息,可以把震中的位置限制在双曲线的一支上,这两个地震台站的位置就是该双曲线的两个焦点.在一次地震预警中,两地震台站和站相距.根据它们收到的信息,可知震中到站与震中到站的距离之差为.据此可以判断,震中到地震台站的距离至少为( )A、 B、 C、 D、6. 已知圆和存在公共点,则m的值不可能为( )A、3 B、 C、5 D、7. 如图,在四面体中,是的中点,设 , , , 则( )
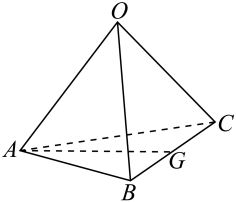 A、 B、 C、 D、8. 对于数列 , 若存在正数 , 使得对一切正整数 , 都有 , 则称数列是有界的.若这样的正数不存在,则称数列是无界的.记数列的前项和为 , 下列结论正确的是( )A、若 , 则数列是无界的 B、若 , 则数列是有界的 C、若 , 则数列是有界的 D、若 , 则数列是有界的
A、 B、 C、 D、8. 对于数列 , 若存在正数 , 使得对一切正整数 , 都有 , 则称数列是有界的.若这样的正数不存在,则称数列是无界的.记数列的前项和为 , 下列结论正确的是( )A、若 , 则数列是无界的 B、若 , 则数列是有界的 C、若 , 则数列是有界的 D、若 , 则数列是有界的二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
-
9. 已知向量 , 则与同向共线的单位向量( )A、 B、 C、 D、10. 已知数列满足 , , 记 , 则( )A、 B、 C、 D、11. 已知直线与圆 , 则下列结论正确的是( )A、存在 , 使得的倾斜角为 B、存在 , 使得的倾斜角为 C、存在 , 使直线与圆相离 D、对任意的 , 直线与圆相交,且时相交弦最短12. 已知双曲线的左、右焦点分别为、 , 左、右顶点分别为、 , 为双曲线右支上的一点,且直线与的斜率之积等于 , 则下列说法正确的是( )A、双曲线的渐近线方程为 B、若 , 且 , 则 C、分别以线段、为直径的两个圆内切 D、
三、填空题:本题共4小题,每小题5分,共20分.
-
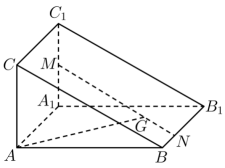
13. 若直线 与直线 平行,则 .14. 已知双曲线的一条渐近线方程为 , 则 .15. 已知数列为 , , , , , 则该数列的一个通项公式可以是 .16. 《九章算术》中的“商功”篇主要讲述了以立体几何为主的各种形体体积的计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵 , 中,M是的中点, , , , 若 , 则 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 已知直线和直线 .(1)、若时,求a的值;(2)、当平行,求两直线 , 的距离.18. 已知直线l:与x轴的交点为A,圆O:经过点A.(1)、求r的值;(2)、若点B为圆O上一点,且直线垂直于直线l,求弦长 .19. 如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=1,BC=2,PA=1.
 (1)、求证:AB⊥PC;(2)、点M在线段PD上,二面角M﹣AC﹣D的余弦值为 , 求三棱锥M﹣ACP体积.20. 已知数列 的前 项和为 . .(1)、求数列 的通项公式;(2)、从下面两个条件中选择一个填在横线上,并完成下面的问题.① , ;② 是 和 的等比中项, .若公差不为0的等差数列 的前 项和为 ,且 ▲ , 求数列 的前 项和 .
(1)、求证:AB⊥PC;(2)、点M在线段PD上,二面角M﹣AC﹣D的余弦值为 , 求三棱锥M﹣ACP体积.20. 已知数列 的前 项和为 . .(1)、求数列 的通项公式;(2)、从下面两个条件中选择一个填在横线上,并完成下面的问题.① , ;② 是 和 的等比中项, .若公差不为0的等差数列 的前 项和为 ,且 ▲ , 求数列 的前 项和 .