2024年北师大版数学七（下）期中专项复习3 平方差公式和完全平方公式

试卷更新日期：2024-03-07 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、 $a^{2} + b^{2} = (a + b)^{2}$ B、 $(x + 2)^{2} = x^{2} + 2 x + 4$ C、 $(x - 6) (x + 6) = x^{2} - 6$ D、 $(x - y)^{2} = (y - x)^{2}$

查看试题解析
2. 我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉 $($ 约 $13$ 世纪 $)$ 所著的 $《$ 详解九章算术 $》$ 一书中，用如图的三角形解释二项和 $(a + b)^{n}$ 的展开式的各项系数，此三角形称为“杨辉三角”，根据“杨辉三角”计算 $(a + b)^{9}$ 的展开式中第三项的系数为（）

A、 $28$ B、 $36$ C、 $45$ D、 $56$

查看试题解析
3. 下列多项式，为完全平方式的是（）

A、 $1 + 4 a^{2}$ B、 $4 b^{2} + 4 b - 1$ C、 $a^{2} - 4 a + 4$ D、 $a^{2} + a b + b^{2}$

查看试题解析
4. 下列各式中，不能用平方差公式计算的是（）

A、 $(- x - y) (x - y)$ B、 $(- x + y) (- x - y)$ C、 $(x + y) (- x + y)$ D、 $(x - y) (- x + y)$

查看试题解析
5. 下列各式中，不能用平方差公式的是（）

A、（4x-3y）（3y-4x） B、（-4x+3y）（4x+3y） C、（-4x+3y）（-4x-3y） D、（4x+3y）（4x-3y）

查看试题解析
6. 下列计算正确的一项是（）

A、 $a^{5} + a^{5} = 2 a^{10}$ B、 $(a + 2) (a - 2) = a^{2} - 4$ C、 $(a - b)^{2} = a^{2} - b^{2}$ D、 $4 a - 2 a = 2$

查看试题解析
7. 下列多项式乘法中可以用平方差公式计算的是（）

A、 $(- a + b) (a - b)$ B、 $(x + 2) (2 + x)$ C、 $(\frac{x}{3} + y) (y - \frac{x}{3})$ D、 $(x - 2) (x + 1)$

查看试题解析
8. 若x²+mx+16是完全平方式，则m的值是（）

A、-2 B、±8 C、2 D、3

查看试题解析
9. 已知 $a b = - 5$ ， $a - b = 6$ ，则 $a^{2} + b^{2} =$ （）

A、13 B、19 C、26 D、37

查看试题解析
10. 下列计算中① $x (2 x^{2} - x + 1) = 2 x^{3} - x^{2} + 1$ ；② ${(a + b)}^{2} = a^{2} + b^{2}$ ；③ ${(x - 4)}^{2} = x^{2} - 4 x + 16$ ；④ $(5 a - 1) (- 5 a - 1) = 25 a^{2} - 1$ ；⑤ ${(- a - b)}^{2} = a^{2} + 2 a b + b^{2}$ ；正确的个数有…（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知 $x^{2} + 2 (m + 1) x + 25$ 是完全平方式，则 $m$ 的值为．

查看试题解析
12. $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{99^{2}}) (1 - \frac{1}{100^{2}})$ =；

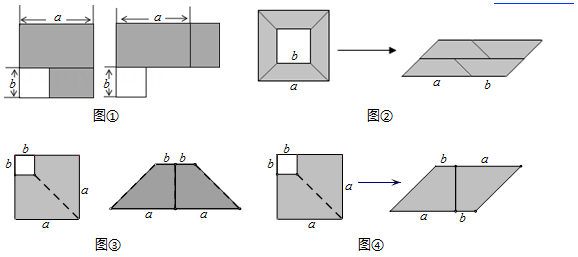
查看试题解析
13. 若 $4 x^{2} - (a - 1) x y + 9 y^{2}$ 是完全平方式，则a＝．

查看试题解析
14. 如图，阴影部分是边长是 $a$ 的大正方形剪去一个边长是 $b$ 的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，给出下列4幅图割拼方法中，其中能够验证平方差公式的有（填序号）

查看试题解析
15. 阅读材料解决问题．
小明遇到下面一个问题：
计算：(2+1)(2²+1)(2⁴+1)(2⁸+1)．
经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：
(2+1)(2²+1)(2⁴+1)(2⁸+1)
=(2-1)(2+1)(2²+1)(2⁴+1)(2⁸+1)
=(2²-1)(2²+1)(2⁴+1)(2⁸+1)
=(2⁴-1)(2⁴+1)(8+1)
=(2⁸-1)(2⁸+1)
=2¹⁶-1．
请你仿照小明解决问题的方法，计算：(6+1)(6²+1)(6⁴+1)(6⁸+1)=

查看试题解析

三、计算题

16. 计算：

(1)、 $(π - 2)^{0} - | 8 | + (\frac{1}{3})^{- 2}$ ；

(2)、 $(2 x)^{3} \cdot (- 3 x y^{2}) \div (- 2 x^{2} y^{2})$ ；

(3)、 $(4 - x)^{2} - (x - 2) (x + 3)$ ；

(4)、 $12 5^{2} - 124 \times 126 . ($ 请用简便运算 $)$

查看试题解析
17. 计算：

(1)、 (π-3)⁰+( $\frac{1}{2}$ )^-2+(-1)²⁰²²；

(2)、x·x²·x³+(x²)³-2(x³)²；

(3)、 (a+3b-2c)(a+3b+2c)；

(4)、 2022²-2021×2023．

查看试题解析

四、解答题

18. 如图，是由四个长为 $m$ ，宽为 $n$ 的小长方形拼成的正方形．

(1)、图中的阴影正方形的边长可表示为 $($ 用含 $m$ ， $n$ 的代数式表示 $)$ ；

(2)、根据图形中的数量关系，请你结合图形直接写出 $(m + n)^{2}$ ， $(m - n)^{2}$ ， $m n$ 之间的一个等量关系；

(3)、根据(2)中的结论，解决下列问题：若 $m + n = 7$ ， $m n = 3$ ，求阴影正方形的面积．

查看试题解析
19. 先化简，再求值： [(x+2y)²-(x-2y)²-(x+2y)(x-2y)-4y²]÷2x，其中x=-2，y= $\frac{1}{2}$ ；

查看试题解析

五、实践探究题

20.

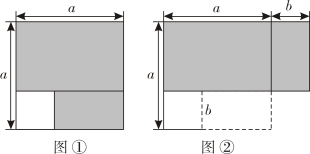(1)、【探究】如图 $①$ ，从边长为 $a$ 的大正方形中剪掉一个边长为 $b$ 的小正方形，将阴影部分沿虚线剪开，拼成图 $②$ 的长方形 $.$ 比较两图的阴影部分面积，可以得到乘法公式： $($ 用字母 $a$ 、 $b$ 表示 $)$ ；

(2)、【应用】请应用这个公式完成下列各题：
$①$ 已知 $2 m - n = 3$ ， $2 m + n = 4$ ，则 $4 m^{2} - n^{2}$ 的值为 ▲ ；
$②$ 计算： $(x - 3) (x + 3) (x^{2} + 9)$ ；

(3)、【拓展】计算 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \cdot \cdot \cdot (2^{32} + 1)$ 的结果为．

查看试题解析
21. 【阅读理解】
完全平方公式： $(a \pm b)^{2} = a^{2} \pm 2 a b + b^{2}$ 适当的变形，可以解决很多的数学问题．
例：若 $a + b = 3$ ， $a b = 1$ ，求 $a^{2} + b^{2}$ 的值．
解： $∵ a + b = 3$ ， $a b = 1$ ，
$∴ (a + b)^{2} = 9$ ， $2 a b = 2$ ．
$∴ (a + b)^{2} = a^{2} + 2 a b + b^{2} = 9$ ．
$∴ a^{2} + b^{2} = 7$ ．
根据上面的解题思路与方法，解决下列问题：

(1)、若 $x + y = 8$ ， $x y = 12$ ，则 $x^{2} + y^{2} =$ ；

(2)、类比应用：
若 $x + y = 4$ ， $x^{2} + y^{2} = 10$ ，求 $x y$ 的值；

(3)、思维拓展：
如图，点 $C$ 是线段 $A B$ 上的一点，以 $A C$ ， $B C$ 为边向两边作正方形，若 $A B = 6$ ，两正方形的面积和 $S_{1} + S_{2} = 18$ ，求图中阴影部分面积．

查看试题解析

六、综合题

22. 阅读下面的材料，然后解答后面的问题：在数学中，“算两次”是一种常用的方法 $.$ 其思想是，对一个具体的量用方法甲来计算，得到的答案是A，而用方法乙计算则得到的答案是B，那么等式 $A = B$ 成立 $.$ 例如，我们运用“算两次”的方法计算图1中最大的正方形的面积，可以得到等式 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ．

(1)、理解：运用“算两次”的方法计算图2中最大的正方形的面积，可以得到的等式是.

(2)、应用：七①班某数学学习小组用8个直角边长为 $a$ 、 $b$ 的全等直角三角形拼成如图3所示的中间内含正方形 $A_{1} B_{1} C_{1} D_{1}$ 与 $A_{2} B_{2} C_{2} D_{2}$ 的正方形 $A B C D$ ，运用“算两次”的方法计算正方形 $A_{2} B_{2} C_{2} D_{2}$ 的面积，可以得到的等式是；

(3)、拓展：如图4，已知 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 6$ ， $B C = 8$ ， $A B = 10$ ，点 $D$ 是 $A B$ 上一动点.求 $C D$ 的最小值．

查看试题解析
23. 如图1是一个长为2a，宽为2b的长方形，沿图中虚线剪开分成四块小长方形，然后按如图2的形状拼成一个正方形．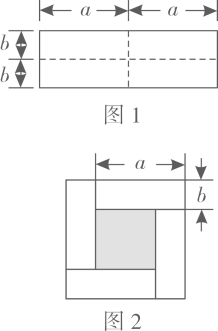

(1)、图2的阴影部分的正方形的边长是．

(2)、用两种不同的方法求图中阴影部分的面积．
【方法1】S_阴影＝；
【方法2】S_阴影＝；

(3)、观察如图2，写出（a+b）² ，（a-b）² ， ab这三个代数式之间的等量关系．

(4)、根据（3）题中的等量关系，解决问题：
若x+y＝10，xy＝16，求x-y的值．

查看试题解析