2024年浙教版数学八年级下学期第三章 数据分析初步 单元测试（培优卷）
试卷更新日期：2024-03-07 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 已知数据x₁，x₂，⋯，xn的平均数是2，则 3x₁-2，3x₂-2，…，3x，-2的平均数是 （ ）A、0 B、2 C、4 D、62. 某超市销售A，B，C，D四种矿泉水，它们的单价依次是5元、3元、2元、1元，某天的销售情况如图所示，则这天销售矿泉水的平均单价是 （ ）
A、1.95元 B、2.15元 C、2.25 元 D、2.75 元3. 某工厂生产质量分别为1g，5g，10g，25 g四种规格的球，现从中取 x个球装到一个空箱子里，这时箱子里球的平均质量为 20g，若再放入一个 25 g的球，此时箱子里球的平均质量变为2lg，则x的值为 （ ）A、3 B、4 C、5 D、64. 5名学生投篮训练，规定每人投10次，记录他们每人投中的次数，得到五个数据，经分析这五个数据的中位数为6，唯一众数是7，则他们投中次数占投篮总次数的百分率可能是（ ）A、40% B、56% C、60% D、62%5. 若数据1，2，3，4，5，x存在唯一的众数，且该组数据的平均数等于众数，则x的值为（ ）A、2 B、3 C、4 D、56. 如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5 分)，则所打分数的众数为（ ）课后延时服务的打分情况扇形统计图
A、5分 B、4分 C、3分 D、45%7. 某射击运动员在训练中射击了10次，成绩如图所示：某射击运动员在训练中射击环数折线统计图
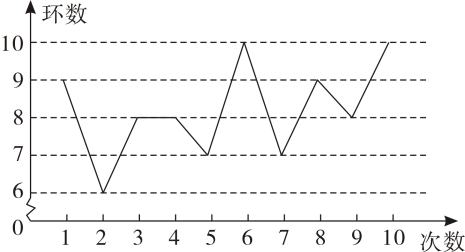
下列结论中，错误的是 （ ）
A、众数是8 B、中位数是8 C、平均数是8.2 D、方差是 1.28. 一组数据2，3，4，5，6的方差是 （ ）A、 B、2 C、4 D、59. 某一公司共有51名员工（包括经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（ ）A、平均数和中位数不变 B、平均数增加，中位数不变 C、平均数不变，中位数增加 D、平均数和中位数都增大10. 若一组数据 ， ， 的平均数为4，方差为3，那么数据 ， ， 的平均数和方差分别是（ ）A、4， 3 B、6 3 C、3 4 D、6
5
二、填空题（每题4分，共24分）
-
11. 某计算机程序第一次算得m个数据的平均数是x，第二次算得另外n个数据的平均数是y，则这(m+n)个数据的平均数是.12. 甲、乙两位同学上学期有5 次数学检测，成绩如下表所示：
第1次
第2次
第3次
第4次
第5次
甲
103分
102分
104分
105分
106分
乙
100分
107分
102分
106分
105 分
(1)、甲、乙两位同学这五次数学检测成绩的平均分分别为.(2)、若前 3次为平时单元考成绩，第 4次为期中考成绩，第 5 次为期末考成绩.规定：平时单元考成绩的平均分占 30%，期中考成绩占20%，期末考成绩占 50%来计算总评成绩，甲、乙两位同学的学期总评成绩更好的是（填“甲”或“乙”）.13. 若一组数据1，2，4，6，x的中位数和平均数相等，则x的值是.14. 有5个不同的整数1，3，5，12，a，其中a是这组数据的中位数，则该组数据的平均数是.15. 为了解“睡眠管理”落实情况，某校随机调查了46名学生每天平均睡眠时间，并将样本数据绘制成如图所示的统计图(其中有两个数据被遮盖).有以下关于睡眠时间的统计量：①平均数，②中位数，③众数，④方差，其中与被遮盖的数据无关的是(填序号).
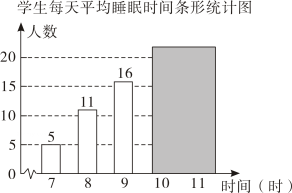
16. 如果一组按从小到大排序的数据a，b，c的平均数是b，方差是S2 ， 那么数据a+99，b+100，c+101的方差将 S2（填“大于”“小于”或“等于”）.三、解答题（共8题，共66分）
-
17. 某公司为提高服务质量，对其某个部门开展了客户满意度问卷调查，客户满意度以分数呈现，满意度从低到高为1分，2分，3分，4分，5分，共5档公司规定：若客户所评分数的平均数或中位数低于3.5分，则该部门需要对服务质量进行整改．工作人员从收回的问卷中随机抽取了20份，如图是根据这20份问卷中的客户所评分数绘制的统计图．
(1)、求客户所评分数的中位数平均数，并判断该部门]是否需要整改．(2)、监督人员从余下的问卷中又随机抽取了1份，与之前的20份合在一起，重新计算后，发现客户所评分数的平均数大于3.55分，求监督人员抽取的问卷所评分数为几分．与(1)相比，中位数是否发生变化？18. 某校要从甲、乙两名队员中选派一人参加射击比赛，甲、乙两名队员在相同的条件下各射击10次，每次命中的环数如下表所示．次数
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
甲成绩(环数)
6
8
7
4
5
6
6
5
6
7
乙成绩(环数)
7
5
6
7
9
5
4
3
6
(1)、已知甲、乙两名队员的射击成绩的平均成绩相等，请补齐乙的成绩．(2)、甲运动员射击训练成绩的众数是 ， 中位数是.(3)、在(1)的情况下，甲、乙两名队员的射击成绩的方差分别是多少？根据计算结果，从平均数和方差的角度分析，谁将被选中．19. 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了 5箭，他们的总成绩(单位：环)相同，小宇根据他们的成绩绘制了尚不完整的统计图表，并计算了甲成绩的平均数和方差(见小宇的作业).甲、乙两人射箭成绩统计表
第1次
第2次
第3次
第4次
第5次
甲
9
4
7
4
6
乙
7
5
7
a
7
小宇的作业：
解
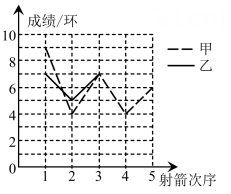(1)、a= ， x₂= ， 甲成绩的众数是 ， 乙成绩的中位数是(2)、请完成图中表示乙成绩变化情况的折线.(3)、①请求出乙成绩的方差，并比较谁的成绩比较稳定.②请你从平均数和方差的角度分析，谁将被选中.
甲、乙两人射箭成绩折线统计图
20. 已知一组数据-1，0，3，5，x 的方差是 ， 求 x 的值.21. 已知一组数据-3，-2，5 ，6，13，x的中位数是2．(1)、求这组数据的平均数；(2)、求这组数据的方差与标准差(结果保留两位小数)22. 某校组织了一次“校徽设计”竞赛活动，邀请5名老师作为专业评委，50名学生代表参与民主测评，且民主测评的结果无弃权票，某作品的评比数据统计如下：专业评委 给分（单位：分） ① 88 ② 87 ③ 94 ④ 91 ⑤ 90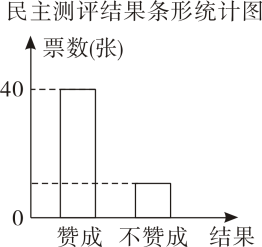 
(1)、求该作品在民主测评中得到“不赞成”的票数.(2)、记“专业评委给分”的平均数为.对于该作品，的值是多少?(3)、记“民主测评得分”为 ， “综合得分”为S，若规定：①=“赞成”的票数×3分+“不赞成”的票数×(-1)分；
②S=0.7+0.3.
求该作品的“综合得分”S的值.
23. 某公司共19名员工，如表是他们月收入的资料．月收入(元)
23000
12000
8000
5500
4600
4200
3700
2500
1800
人数
1
1
1
1
5
3
2
3
2
(1)、该公司员工月收入的众数是元，中位数是元(2)、根据上表，可以算得该公司员工月收入的平均数为5 400元你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适？说明理由．24.某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小明已根据成绩表算出了甲成绩的平均数和方差，请你完成下面两个问题．
甲、乙两人射箭成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
m
7
小明的正确计算：
=（9+4+7+6）=6（环），s甲2=[（9﹣6）2+（4﹣6）2+（7﹣6）2+（4﹣6）2+（6﹣6）2]=3.6（环2）（1）求m的值和乙的平均数及方差；
（2）请你从平均数和方差的角度分析，谁将被选中．