浙江省杭州市钱江区(闻堰)2023-2024学年八年级上册数学期中试卷
试卷更新日期:2024-03-07 类型:期中考试
一、仔细选一选(本题有10个小题,每小题3分,共30分。下面每小题给出的四个选项中,只有一个是正确的.)
-
1. 下列长度的三段钢条,不能组成一个三角形框架的是(单位:cm)( )A、2,3,4 B、3,7,7 C、2,2,6 D、5,6,72. 下列四个图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列命题中,是真命题的是( )A、有两条边和一个角对应相等的两个三角形全等 B、等腰三角形的对称轴是底边上的高线 C、在同一平面内,过一点有且只有一条直线垂直于已知直线 D、同位角相等4. 在 中, ,则 等于( )A、 B、 C、 D、5. 下列条件中,能判定为直角三角形的是( )A、 B、 C、:::: D、6. 若直角三角形的两边长分别是5和12,则它的斜边长是( )A、13 B、13或 C、 D、12或137. 如图所示,已知 , 那么添加下列一个条件后,仍无法判定≌的是( )
3. 下列命题中,是真命题的是( )A、有两条边和一个角对应相等的两个三角形全等 B、等腰三角形的对称轴是底边上的高线 C、在同一平面内,过一点有且只有一条直线垂直于已知直线 D、同位角相等4. 在 中, ,则 等于( )A、 B、 C、 D、5. 下列条件中,能判定为直角三角形的是( )A、 B、 C、:::: D、6. 若直角三角形的两边长分别是5和12,则它的斜边长是( )A、13 B、13或 C、 D、12或137. 如图所示,已知 , 那么添加下列一个条件后,仍无法判定≌的是( ) A、 B、 C、 D、8. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A、 B、 C、 D、8. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )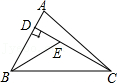 A、10 B、7 C、5 D、49. 如图,在中, , , 以顶点为圆心,长为半径画弧,交边于点 , 再分别以点 , 为圆心,适当的长度为半径画弧,两弧交于点 , 作射线交边于点 , 点为边上的动点,若 , 则的取值范围是( )
A、10 B、7 C、5 D、49. 如图,在中, , , 以顶点为圆心,长为半径画弧,交边于点 , 再分别以点 , 为圆心,适当的长度为半径画弧,两弧交于点 , 作射线交边于点 , 点为边上的动点,若 , 则的取值范围是( ) A、 B、 C、 D、3≤PF≤510. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BGC=90+ ∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则 = mn.其中正确的结论有( )
A、 B、 C、 D、3≤PF≤510. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BGC=90+ ∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则 = mn.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、认真填一填(本题有6个小题,每小题4分,共24分)
-
11. 命题“对顶角相等”的逆命题是12. 已知等腰三角形的一个内角为110°,则等腰三角形的底角的度数为.13. 如图,在△ABC中,∠BAC=90°,AB=6,BC=10,EF垂直平分BC,点P为直线EF上的任一点,则△ABP周长的最小值是 .
 14. 如图,已知∠OAB=∠OBC=∠OCD=90°,AB=BC=CD=1,OA=3,则OD=.
14. 如图,已知∠OAB=∠OBC=∠OCD=90°,AB=BC=CD=1,OA=3,则OD=. 15. 如图,在△ABC中,D是B C上一点,AB=AD,E,F分别是AC,BD的中点,EF=3,则AC的长是.
15. 如图,在△ABC中,D是B C上一点,AB=AD,E,F分别是AC,BD的中点,EF=3,则AC的长是. 16. 如图,在△ABC中,D为边AC上一点,且BD平分∠ABC,过A作AE⊥BD于 点E.若∠ABC+4∠C=180°,AB=5,BC=12,则AE= .
16. 如图,在△ABC中,D为边AC上一点,且BD平分∠ABC,过A作AE⊥BD于 点E.若∠ABC+4∠C=180°,AB=5,BC=12,则AE= .
三、全面答一答(本大题有7个小题,共66分)
-
17. 如图,CD是△ABC的AB边上的中线,CD=AB,求证:△ABC是直角三角形.

将下面证明的过程补充完整.
证明:∵CD是AB边上的中线 (已知),
∴AD=BD= ▲ ( ).
∵CD=AB,
∴CD=AD .
∴∠A=∠▲( ).
同理,∠B=∠BCD .
∵∠A +∠B+∠ACD+∠BCD=180° ( ),
∴∠A +∠B=∠ACD+∠BCD=80 =90°.
∴△ABC是直角三角形( ).
18. (如图,∠AOB=90° , 且OB=6. (1)、只用直尺(没有刻度)和圆规,求作一个点P , 使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):
(1)、只用直尺(没有刻度)和圆规,求作一个点P , 使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):①点P到0 , B两点的距离相等;
②点P到∠AOB的两边的距离相等.
(2)、在(1)作出点P后,写出OP的长 .19. 如图:在△ABC中,AB=AD=CD. (1)、若∠C=36°,求∠B的度数.(2)、若∠BAD=x°,∠C=y°, 求x和y的数量关系(用x的代数式表示y).20. 如图,在长方形ABCD中, AD=BC=6(cm),点P从点B出发,以 1 (cm/s)的速度沿BC向点C运动,设点 P的运动时间为t(s):
(1)、若∠C=36°,求∠B的度数.(2)、若∠BAD=x°,∠C=y°, 求x和y的数量关系(用x的代数式表示y).20. 如图,在长方形ABCD中, AD=BC=6(cm),点P从点B出发,以 1 (cm/s)的速度沿BC向点C运动,设点 P的运动时间为t(s): (1)、经过t秒后,CP=厘米;(2)、当△ABP≌△DCP时,此时t= 秒;(3)、在(2)的条件下,当∠APD=90°时,求AB的长;21. 在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E, EF⊥AB于点F,EG⊥AG交AC的延长线于点G.求证:
(1)、经过t秒后,CP=厘米;(2)、当△ABP≌△DCP时,此时t= 秒;(3)、在(2)的条件下,当∠APD=90°时,求AB的长;21. 在△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E, EF⊥AB于点F,EG⊥AG交AC的延长线于点G.求证: (1)、EF=EG.(2)、AB-AC=2BF.22. 如图,这是某市工业开发区设计图纸的局部平面图,直线AB是一条河流,河旁边建有一个工厂P,点O,E在直线AB上,O是工厂P的进水口,E是污水净化后的出水口,且PE⊥AB,现计划在河旁边工厂P的同侧再建一座工厂Q,设计要求是:工厂Q也从点O处引水,OQ⊥OP,OQ=OP,污水净化后的排污出口为AB上的点F处,且FQ⊥AB.
(1)、EF=EG.(2)、AB-AC=2BF.22. 如图,这是某市工业开发区设计图纸的局部平面图,直线AB是一条河流,河旁边建有一个工厂P,点O,E在直线AB上,O是工厂P的进水口,E是污水净化后的出水口,且PE⊥AB,现计划在河旁边工厂P的同侧再建一座工厂Q,设计要求是:工厂Q也从点O处引水,OQ⊥OP,OQ=OP,污水净化后的排污出口为AB上的点F处,且FQ⊥AB. (1)、 请根据设计要求把图形补充完整(不需要尺规作图)。(2)、已知QF=350米,PE=150米,求两个出水口E,F之间的距离(不计河的宽度).23. 如图一,△ABC中,D是BC 的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G, DE⊥DF,交AB于点E,连结EG、EF.
(1)、 请根据设计要求把图形补充完整(不需要尺规作图)。(2)、已知QF=350米,PE=150米,求两个出水口E,F之间的距离(不计河的宽度).23. 如图一,△ABC中,D是BC 的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G, DE⊥DF,交AB于点E,连结EG、EF. (1)、求证:BG=CF;(2)、如图二,当∠A=90°时,猜想BE,CF,EF的数量关系,并说明理由;(3)、如图三,在(2)的条件下,当AB=AC时,求证ED=FD.
(1)、求证:BG=CF;(2)、如图二,当∠A=90°时,猜想BE,CF,EF的数量关系,并说明理由;(3)、如图三,在(2)的条件下,当AB=AC时,求证ED=FD.