2023年湖北省中考数学真题分类汇编:03 函数
试卷更新日期:2024-03-06 类型:二轮复习
一、选择题
-
1. 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系().下列反映电流I与电阻R之间函数关系的图象大致是( )A、
 B、
B、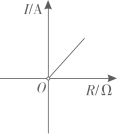 C、
C、 D、
D、 2. 函数的自变量的取值范围是( )A、 B、 C、且 D、3. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位: )是反比例函数关系,它的图象如图所示.则这个反比例函数的解析式为( )
2. 函数的自变量的取值范围是( )A、 B、 C、且 D、3. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位: )是反比例函数关系,它的图象如图所示.则这个反比例函数的解析式为( )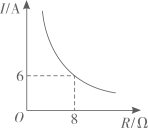 A、 B、 C、 D、4. 已知二次函数的图象经过三点 , , , 且对称轴为直线有以下结论:;;当 , 时,有;对于任何实数 , 关于的方程必有两个不相等的实数根其中结论正确的有( )A、个 B、个 C、个 D、个5. 如图,在平面直角坐标系中,O为坐标原点,抛物线的对称轴为 , 与x轴的一个交点位于 , 两点之间.下列结论:①; ②;③; ④若 , 为方程的两个根,则 . 其中正确的有( )个.
A、 B、 C、 D、4. 已知二次函数的图象经过三点 , , , 且对称轴为直线有以下结论:;;当 , 时,有;对于任何实数 , 关于的方程必有两个不相等的实数根其中结论正确的有( )A、个 B、个 C、个 D、个5. 如图,在平面直角坐标系中,O为坐标原点,抛物线的对称轴为 , 与x轴的一个交点位于 , 两点之间.下列结论:①; ②;③; ④若 , 为方程的两个根,则 . 其中正确的有( )个. A、1 B、2 C、3 D、46. 如图,取一根长的匀质木杆,用细绳绑在木杆的中点O并将其吊起来,在中点O的左侧距离中点处挂一个重的物体,在中点O的右侧用一个弹簧秤向下拉,使木杆处于水平状态.弹簧秤与中点O的距离L(单位:)及弹簧秤的示数F(单位:N)满足 . 以L的数值为横坐标,F的数值为纵坐标建立直角坐标系.则F关于L的函数图象大致是( )
A、1 B、2 C、3 D、46. 如图,取一根长的匀质木杆,用细绳绑在木杆的中点O并将其吊起来,在中点O的左侧距离中点处挂一个重的物体,在中点O的右侧用一个弹簧秤向下拉,使木杆处于水平状态.弹簧秤与中点O的距离L(单位:)及弹簧秤的示数F(单位:N)满足 . 以L的数值为横坐标,F的数值为纵坐标建立直角坐标系.则F关于L的函数图象大致是( ) A、
A、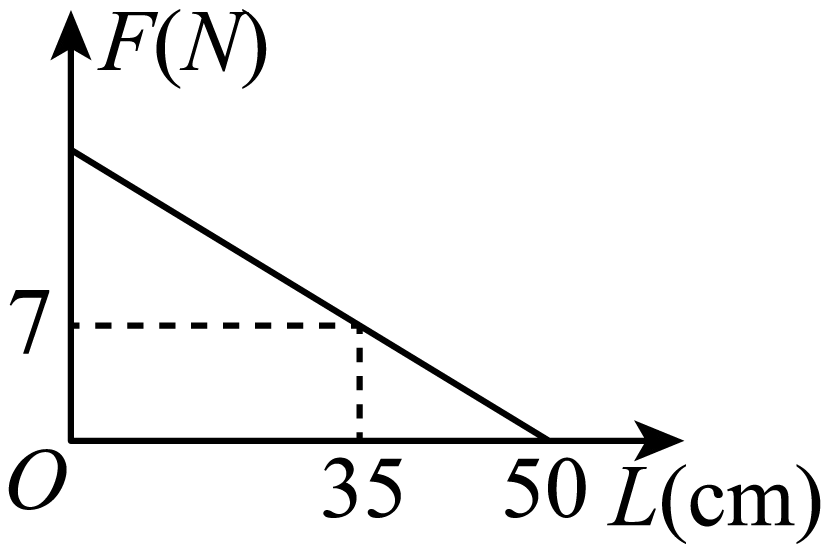 B、
B、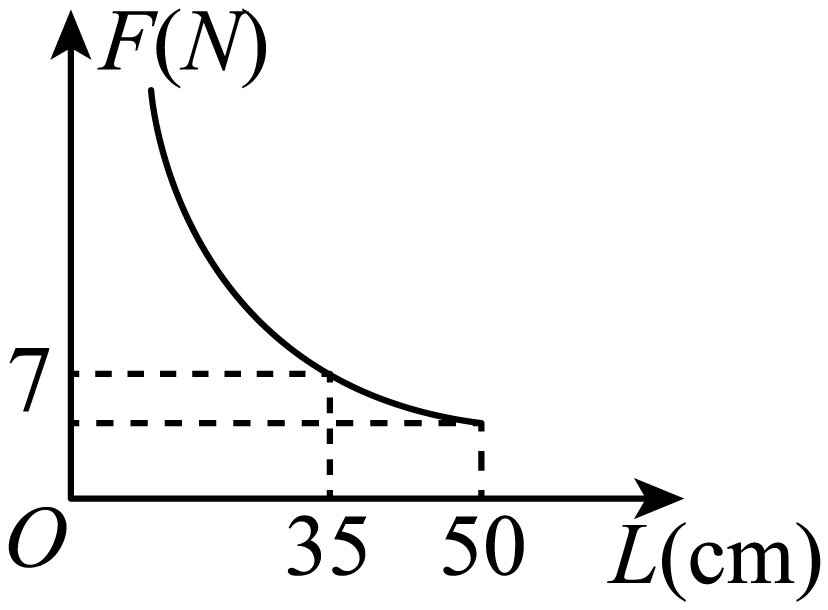 C、
C、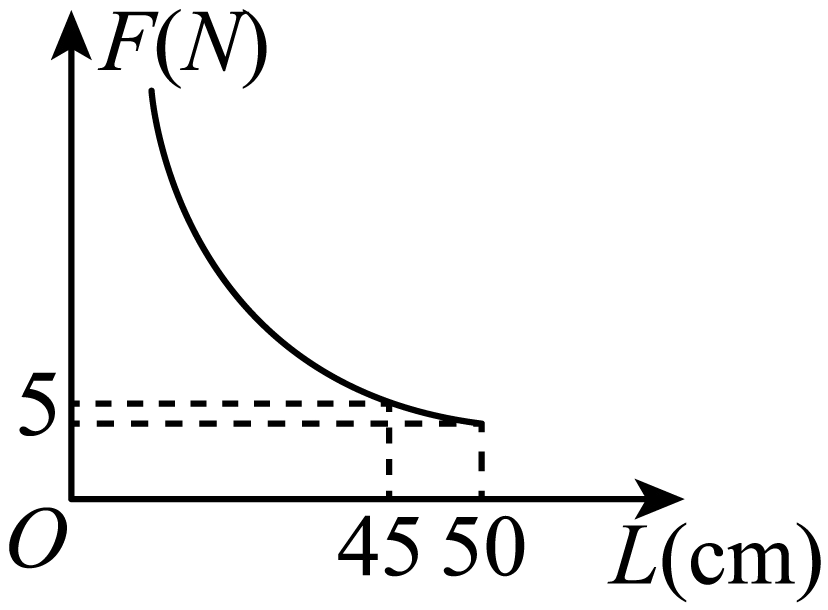 D、
D、 7. 已知二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列论中:①;②若点均在该二次函数图象上,则;③若m为任意实数,则;④方程的两实数根为 , 且 , 则 . 正确结论的序号为( )A、①②③ B、①③④ C、②③④ D、①④8. 象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( )
7. 已知二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列论中:①;②若点均在该二次函数图象上,则;③若m为任意实数,则;④方程的两实数根为 , 且 , 则 . 正确结论的序号为( )A、①②③ B、①③④ C、②③④ D、①④8. 象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( ) A、y=x+1 B、y=x-1 C、y=2x+1 D、y=2x-19. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且过点(-1,0),顶点在第一象限,其部分图象如图所示.给出以下结论:①ab<0;②4a+2b+c>0;③3a+c>0;④若A( , ),B( , )(其中<)是抛物线上的两点,且+>2,则> , 其中正确的选项是( )
A、y=x+1 B、y=x-1 C、y=2x+1 D、y=2x-19. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且过点(-1,0),顶点在第一象限,其部分图象如图所示.给出以下结论:①ab<0;②4a+2b+c>0;③3a+c>0;④若A( , ),B( , )(其中<)是抛物线上的两点,且+>2,则> , 其中正确的选项是( )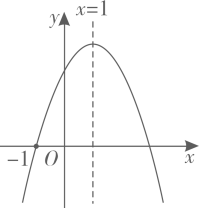 A、①②③ B、①③④ C、②③④ D、①②④10. 如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为(细实线)表示铁桶中水面高度,(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则随时间变化的函数图象大致为( )
A、①②③ B、①③④ C、②③④ D、①②④10. 如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为(细实线)表示铁桶中水面高度,(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则随时间变化的函数图象大致为( ) A、
A、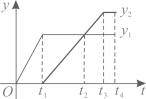 B、
B、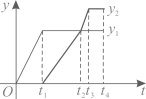 C、
C、 D、
D、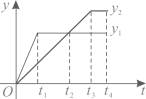 11. 拋物线与轴相交于点 . 下列结论:
11. 拋物线与轴相交于点 . 下列结论:①;②;③;④若点在抛物线上,且 , 则 . 其中正确的结论有( )
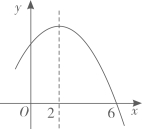
A、1个 B、2个 C、3个 D、4个12. 如图,直线分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转得到△CAD,则点B的对应点D的坐标是( ) A、(2,5) B、(3,5) C、(5,2) D、( , 2)13. 已知点在直线上,点在抛物线上,若且 , 则的取值范围是( )A、 B、 C、 D、14. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线 . 则下列结论正确的有( )
A、(2,5) B、(3,5) C、(5,2) D、( , 2)13. 已知点在直线上,点在抛物线上,若且 , 则的取值范围是( )A、 B、 C、 D、14. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线 . 则下列结论正确的有( )①;
②;
③方程的两个根为;
④抛物线上有两点和 , 若且 , 则 .
 A、1个 B、2个 C、3个 D、4个15. 已知蓄电池的电压为定值,使用某蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示,则当电阻为时,电流为( )
A、1个 B、2个 C、3个 D、4个15. 已知蓄电池的电压为定值,使用某蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示,则当电阻为时,电流为( )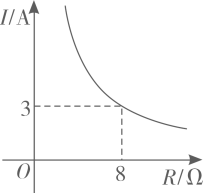 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16. 如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 , 则铅球推出的距离m.
 17. 如图,点和在反比例函数的图象上,其中过点作轴于点 , 则的面积为;若的面积为 , 则 .
17. 如图,点和在反比例函数的图象上,其中过点作轴于点 , 则的面积为;若的面积为 , 则 . 18. 如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1·k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是 .
18. 如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1·k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是 . 19. 在平面直角坐标系中,若反比例函数的图象经过点和点 , 则的面积为 .20. 如图,点A(2,2)在双曲线上,将直线OA向上平移若干个单位长度交y轴于点B,交双曲线于点C. 若BC=2,则点C的坐标是 .
19. 在平面直角坐标系中,若反比例函数的图象经过点和点 , 则的面积为 .20. 如图,点A(2,2)在双曲线上,将直线OA向上平移若干个单位长度交y轴于点B,交双曲线于点C. 若BC=2,则点C的坐标是 .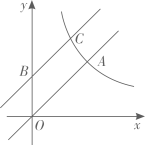 21. 抛物线(是常数,)经过三点,且 . 下列四个结论:
21. 抛物线(是常数,)经过三点,且 . 下列四个结论:①;
②;
③当时,若点在该抛物线上,则;
④若关于的一元二次方程有两个相等的实数根,则 .
其中正确的是(填写序号).
22. 我国古代数学经典著作《九章算术》记载:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”如图是善行者与不善行者行走路程(单位:步)关于善行者的行走时间的函数图象,则两图象交点的纵坐标是 .
三、解答题
-
23. 如图,在平面直角坐标系中,O为坐标原点,直线交y轴于点A , 交x轴于点B , 与双曲线在一,三象限分别交于C , D两点, , 连接 , .
 (1)、求k的值;(2)、求的面积.24. 某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为万元件设第个生产周期设备的售价为万元件,售价与之间的函数解析式是 , 其中是正整数当时,;当时, .(1)、求 , 的值;(2)、设第个生产周期生产并销售完设备的数量为件,且与满足关系式 .
(1)、求k的值;(2)、求的面积.24. 某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为万元件设第个生产周期设备的售价为万元件,售价与之间的函数解析式是 , 其中是正整数当时,;当时, .(1)、求 , 的值;(2)、设第个生产周期生产并销售完设备的数量为件,且与满足关系式 .当时,工厂第几个生产周期获得的利润最大?最大的利润是多少万元?
当时,若有且只有个生产周期的利润不小于万元,求实数的取值范围.
25. 如图,在平面直角坐标系中,抛物线与轴交于两点 , , 与轴交于点 . (1)、求此抛物线的解析式;(2)、已知抛物线上有一点 , 其中 , 若 , 求的值;(3)、若点 , 分别是线段 , 上的动点,且 , 求的最小值.26. 在平面直角坐标系中,为坐标原点,已知抛物线与轴交于点 , 抛物线的对称轴与轴交于点 .
(1)、求此抛物线的解析式;(2)、已知抛物线上有一点 , 其中 , 若 , 求的值;(3)、若点 , 分别是线段 , 上的动点,且 , 求的最小值.26. 在平面直角坐标系中,为坐标原点,已知抛物线与轴交于点 , 抛物线的对称轴与轴交于点 .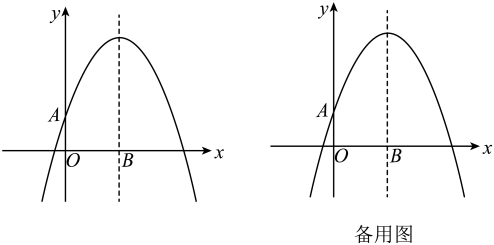 (1)、如图,若 , 抛物线的对称轴为 . 求抛物线的解析式,并直接写出时的取值范围;(2)、在(1)的条件下,若为轴上的点,为轴上方抛物线上的点,当为等边三角形时,求点 , 的坐标;(3)、若抛物线经过点 , , , 且 , 求正整数m , n的值.27. 为积极响应州政府“悦享成长·书香恩施”的号召,学校组织150名学生参加朗诵比赛,因活动需要,计划给每个学生购买一套服装.经市场调查得知,购买1套男装和1套女装共需220元;购买6套男装与购买5套女装的费用相同.(1)、男装、女装的单价各是多少?(2)、如果参加活动的男生人数不超过女生人数的 , 购买服装的总费用不超过17000元,那么学校有几种购买方案?怎样购买才能使费用最低,最低费用是多少?
(1)、如图,若 , 抛物线的对称轴为 . 求抛物线的解析式,并直接写出时的取值范围;(2)、在(1)的条件下,若为轴上的点,为轴上方抛物线上的点,当为等边三角形时,求点 , 的坐标;(3)、若抛物线经过点 , , , 且 , 求正整数m , n的值.27. 为积极响应州政府“悦享成长·书香恩施”的号召,学校组织150名学生参加朗诵比赛,因活动需要,计划给每个学生购买一套服装.经市场调查得知,购买1套男装和1套女装共需220元;购买6套男装与购买5套女装的费用相同.(1)、男装、女装的单价各是多少?(2)、如果参加活动的男生人数不超过女生人数的 , 购买服装的总费用不超过17000元,那么学校有几种购买方案?怎样购买才能使费用最低,最低费用是多少?四、综合题
-
28. 加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位;元/)与其种植面积x(单位:)的函数关系如图所示,其中;乙种蔬菜的种植成本为50元/ .
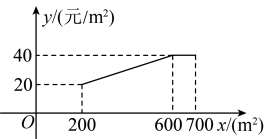 (1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?29. 已知抛物线与x轴交于两点,与y轴交于点 , 点P为第一象限抛物线上的点,连接 .
(1)、当时,元/;(2)、设2023年甲乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小?(3)、学校计划今后每年在这土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降,若甲种蔬菜种植成本平均每年下降 , 乙种蔬菜种植成本平均每年下降 , 当a为何值时,2025年的总种植成本为元?29. 已知抛物线与x轴交于两点,与y轴交于点 , 点P为第一象限抛物线上的点,连接 .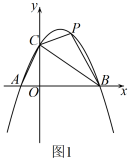
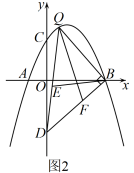
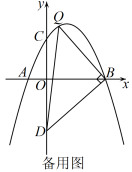 (1)、直接写出结果; , , 点A的坐标为 , ;(2)、如图1,当时,求点P的坐标;(3)、如图2,点D在y轴负半轴上, , 点Q为抛物线上一点, , 点E,F分别为的边上的动点, , 记的最小值为m.
(1)、直接写出结果; , , 点A的坐标为 , ;(2)、如图1,当时,求点P的坐标;(3)、如图2,点D在y轴负半轴上, , 点Q为抛物线上一点, , 点E,F分别为的边上的动点, , 记的最小值为m.①求m的值;
②设的面积为S,若 , 请直接写出k的取值范围.
30. 如图,一次函数与函数为的图象交于两点. (1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.31. 1号探测气球从海拔10m处出发,以1m/min的速度竖直上升.与此同时,2号探测气球从海拔20m处出发,以am/min的速度竖直上升.两个气球都上升了1h.1号、2号气球所在位置的海拔 , (单位:m)与上升时间x(单位:min)的函数关系如图所示.请根据图象回答下列问题:
(1)、求这两个函数的解析式;(2)、根据图象,直接写出满足时x的取值范围;(3)、点P在线段上,过点P作x轴的垂线,垂足为M,交函数的图象于点Q,若面积为3,求点P的坐标.31. 1号探测气球从海拔10m处出发,以1m/min的速度竖直上升.与此同时,2号探测气球从海拔20m处出发,以am/min的速度竖直上升.两个气球都上升了1h.1号、2号气球所在位置的海拔 , (单位:m)与上升时间x(单位:min)的函数关系如图所示.请根据图象回答下列问题: (1)、a= , b;(2)、请分别求出 , 与x的函数关系式;(3)、当上升多长时间时,两个气球的海拔竖直高度差为5m?32. 某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表:
(1)、a= , b;(2)、请分别求出 , 与x的函数关系式;(3)、当上升多长时间时,两个气球的海拔竖直高度差为5m?32. 某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表:时间:第x(天)
日销售价(元/件)
50
日销售量(件)
( , x为整数)
设该商品的日销售利润为w元.
(1)、直接写出w与x的函数关系式;(2)、该商品在第几天的日销售利润最大?最大日销售利润是多少?33. 如图1,在平面直角坐标系中,已知抛物线与轴交于点 , 与轴交于点 , 顶点为 , 连接 . (1)、抛物线的解析式为;(直接写出结果)(2)、在图1中,连接并延长交的延长线于点 , 求的度数;(3)、如图2,若动直线与抛物线交于两点(直线与不重合),连接 , 直线与交于点 . 当时,点的横坐标是否为定值,请说明理由.34. 已知:y关于x的函数 .
(1)、抛物线的解析式为;(直接写出结果)(2)、在图1中,连接并延长交的延长线于点 , 求的度数;(3)、如图2,若动直线与抛物线交于两点(直线与不重合),连接 , 直线与交于点 . 当时,点的横坐标是否为定值,请说明理由.34. 已知:y关于x的函数 . (1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .
(1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .①当点P为抛物线顶点时,求△PBC的面积;
②探究直线l在运动过程中,-是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
35. 荆州古城旁“荆街”某商铺打算购进A,B两种文创饰品对游客销售.已知1400元采购A种的件数是630元采购B种件数的2倍,A种的进价比B种的进价每件多1元,两种饰品的售价均为每件15元;计划采购这两种饰品共600件,采购B种的件数不低于390件,不超过A种件数的4倍.(1)、求A,B饰品每件的进价分别为多少元?(2)、若采购这两种饰品只有一种情况可优惠,即一次性采购A种超过150件时,A种超过的部分按进价打6折.设购进A种饰品x件,①求x的取值范围;②设计能让这次采购的饰品获利最大的方案,并求出最大利润.36. 函数的图象可以由函数的图象左右平移得到.(1)、将函数的图象向右平移4个单位得到函数的图象,则;(2)、下列关于函数的性质:①图象关于点对称;②随的增大而减小;③图象关于直线对称;④的取值范围为 . 其中说法正确的是(填写序号);(3)、根据(1)中的值,写出不等式的解集: .37. “端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进一种品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒,根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒,设每盒售价为x元,日销售量为p盒.(1)、当时,;(2)、当每盒售价定为多少元时,日销售利润W(元)最大?最大利润是多少?(3)、小强说:“当日销售利润最大时,日销售额不是最大,”小红说:“当日销售利润不低于8000元时,每盒售价x的范围为 . ”你认为他们的说法正确吗?若正确,请说明理由;若不正确,请直接写出正确的结论.38. 为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为 , 已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元(1)、 , ;(2)、求第x天的销售额W元与x之间的函数关系式;(3)、在试销售的30天中,销售额超过1000元的共有多少天?39. 如图1,平面直角坐标系中,抛物线过点 , 和 , 连接 , 点为抛物线上一动点,过点作轴交直线于点 , 交轴于点 . (1)、直接写出抛物线和直线的解析式;(2)、如图2,连接 , 当为等腰三角形时,求的值;(3)、当点在运动过程中,在轴上是否存在点 , 使得以 , , 为顶点的三角形与以 , , 为顶点的三角形相似(其中点与点相对应),若存在,直接写出点和点的坐标;若不存在,请说明理由.40. 抛物线交轴于两点(在的左边),交轴于点 .
(1)、直接写出抛物线和直线的解析式;(2)、如图2,连接 , 当为等腰三角形时,求的值;(3)、当点在运动过程中,在轴上是否存在点 , 使得以 , , 为顶点的三角形与以 , , 为顶点的三角形相似(其中点与点相对应),若存在,直接写出点和点的坐标;若不存在,请说明理由.40. 抛物线交轴于两点(在的左边),交轴于点 .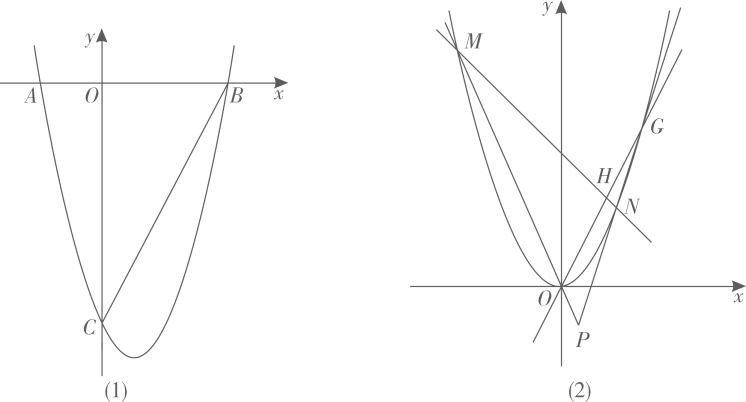 (1)、直接写出三点的坐标;(2)、如图(1),作直线 , 分别交轴,线段 , 抛物线于三点,连接 . 若与相似,求的值;(3)、如图(2),将抛物线平移得到抛物线 , 其顶点为原点.直线与抛物线交于两点,过的中点作直线(异于直线)交抛物线于两点,直线与直线交于点 . 问点是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.
(1)、直接写出三点的坐标;(2)、如图(1),作直线 , 分别交轴,线段 , 抛物线于三点,连接 . 若与相似,求的值;(3)、如图(2),将抛物线平移得到抛物线 , 其顶点为原点.直线与抛物线交于两点,过的中点作直线(异于直线)交抛物线于两点,直线与直线交于点 . 问点是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.