2023年湖北省中考数学真题分类汇编：02 方程和不等式

试卷更新日期：2024-03-06 类型：二轮复习

进入出卷网下载

一、选择题

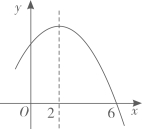
1. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根木条，绳子还余4.5尺；将绳子对折再量木条，木条余1尺，问木条长多少尺？若设木条长x尺，绳子长y尺，则可列方程组为（）

A、 ${\begin{cases} y = x + 4.5 \\ 0.5 y = x - 1 \end{cases}$ B、 ${\begin{cases} y = x - 4.5 \\ 0.5 y = x + 1 \end{cases}$ C、 ${\begin{cases} y = x + 4.5 \\ y = 2 x - 1 \end{cases}$ D、 ${\begin{cases} y = x - 4.5 \\ y = 2 x - 1 \end{cases}$

查看试题解析
2. 分式方程 $\frac{x}{x - 3} = \frac{x + 1}{x - 1}$ 的解是（　　）

A、 $x = 3$ B、 $x = - 3$ C、 $x = 2$ D、 $x = 0$

查看试题解析
3. 不等式组 ${\begin{array}{l} 3 x - 1 \geq x + 1 \\ x + 4 > 4 x - 2 \end{array}$ 的解集是（）

A、 $1 \leq x < 2$ B、 $x \leq 1$ C、 $x > 2$ D、 $1 < x \leq 2$

查看试题解析
4. 为了落实“双减”政策，进一步丰富文体活动，学校准备购进一批篮球和足球，已知每个篮球的价格比每个足球的价格多20元，用1500元购进篮球的数量比用800元购进足球的数量多5个，如果设每个足球的价格为x元，那么可列方程为（）

A、 $\frac{1500}{x + 20} - \frac{800}{x} = 5$ B、 $\frac{1500}{x - 20} - \frac{800}{x} = 5$ C、 $\frac{800}{x} - \frac{1500}{x + 20} = 5$ D、 $\frac{800}{x} - \frac{1500}{x - 20} = 5$

查看试题解析
5. 如图，已知开口向下的抛物线 $y = a x^{2} + b x + c$ 与x轴交于点 $(6 ， 0)$ ，对称轴为直线 $x = 2$ ．则下列结论正确的有（）
① $a b c < 0$ ；

② $a - b + c > 0$ ；

③方程 $c x^{2} + b x + a = 0$ 的两个根为 $x_{1} = \frac{1}{2} ， x_{2} = - \frac{1}{6}$ ；

④抛物线上有两点 $P (x_{1} ， y_{1})$ 和 $Q (x_{2} ， y_{2})$ ，若 $x_{1} < 2 < x_{2}$ 且 $x_{1} + x_{2} > 4$ ，则 $y_{1} < y_{2}$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 甲、乙两个工程队共同修一条道路，其中甲工程队需要修9千米，乙工程队需要修12千米．已知乙工程队每个月比甲工程队多修1千米，最终用的时间比甲工程队少半个月．若设甲工程队每个月修x千米，则可列出方程为（）

A、 $\frac{9}{x} - \frac{12}{x + 1} = \frac{1}{2}$ B、 $\frac{12}{x + 1} - \frac{9}{x} = \frac{1}{2}$ C、 $\frac{9}{x + 1} - \frac{12}{x} = \frac{1}{2}$ D、 $\frac{12}{x} - \frac{9}{x + 1} = \frac{1}{2}$

查看试题解析
7. 解不等式 $\frac{1 + 4 x}{3} > x - 1$ ，下列在数轴上表示的解集正确的是（）．

A、 B、 C、 D、

查看试题解析

二、填空题

8. 已知一元二次方程 $x^{2} - 3 x + k = 0$ 的两个实数根为 $x_{1} ， x_{2}$ ，若 $x_{1} x_{2} + 2 x_{1} + 2 x_{2} = 1$ ，则实数 $k =$ ．

查看试题解析
9. 若实数a、b分别满足a²-3a+2=0，b²-3b+2=0，且a≠b，则 $\frac{1}{a} + \frac{1}{b}$ = ．

查看试题解析
10. 已知一元二次方程x²-3x＋1＝0有两个实数根x₁ ， x₂ ，则x₁＋x₂-x₁x₂的值等于．

查看试题解析
11. 已知 $x_{1}$ 、 $x_{2}$ 是方程 $2 x^{2} - 3 x + 1 = 0$ 的两根，则代数式 $\frac{x_{1} + x_{2}}{1 + x_{1} x_{2}}$ 的值为．

查看试题解析

三、计算题

12.

(1)、计算： $(12 x^{4} + 6 x^{2}) \div 3 x - (- 2 x)^{2} (x + 1)$ ；

(2)、解分式方程： $\frac{5}{x^{2} + x} - \frac{1}{x^{2} - x} = 0$ ．

查看试题解析

四、解答题

13. 为积极响应州政府“悦享成长·书香恩施”的号召，学校组织150名学生参加朗诵比赛，因活动需要，计划给每个学生购买一套服装．经市场调查得知，购买1套男装和1套女装共需220元；购买6套男装与购买5套女装的费用相同．

(1)、男装、女装的单价各是多少？

(2)、如果参加活动的男生人数不超过女生人数的 $\frac{2}{3}$ ，购买服装的总费用不超过17000元，那么学校有几种购买方案？怎样购买才能使费用最低，最低费用是多少？

查看试题解析
14. 关于 $x$ 的一元二次方程 $x^{2} + m x - 1 = 0$ ，当 $m = 1$ 时，该方程的正根称为黄金分割数 $.$ 宽与长的比是黄金分割数的矩形叫做黄金矩形，希腊的帕特农神庙采用的就是黄金矩形的设计；我国著名数学家华罗庚的优选法中也应用到了黄金分割数．

(1)、求黄金分割数；

(2)、已知实数 $a$ ， $b$ 满足： $a^{2} + m a = 1$ ， $b^{2} - 2 m b = 4$ ，且 $b \neq - 2 a$ ，求 $a b$ 的值；

(3)、已知两个不相等的实数 $p$ ， $q$ 满足： $p^{2} + n p - 1 = q$ ， $q^{2} + n q - 1 = p$ ，求 $p q - n$ 的值．

查看试题解析

五、综合题

15. 为纪念爱国诗人屈原，人们有了端午节吃粽子的习俗．某顾客端午节前在超市购买豆沙粽10个，肉粽12个，共付款136元，已知肉粽单价是豆沙粽的2倍．

(1)、求豆沙粽和肉粽的单价；

(2)、超市为了促销，购买粽子达20个及以上时实行优惠，下表列出了小欢妈妈、小乐妈妈的购买数量（单位：个）和付款金额（单位：元）；

	豆沙粽数量	肉粽数量	付款金额
小欢妈妈	20	30	270
小乐妈妈	30	20	230

①根据上表，求豆沙粽和肉粽优惠后的单价；

②为进一步提升粽子的销量，超市将两种粽子打包成A，B两种包装销售，每包都是40个粽子（包装成本忽略不计），每包的销售价格按其中每个粽子优惠后的单价合计．A，B两种包装中分别有m个豆沙粽，m个肉粽，A包装中的豆沙粽数量不超过肉粽的一半．端午节当天统计发现，A，B两种包装的销量分别为 $(80 - 4 m)$ 包， $(4 m + 8)$ 包，A，B两种包装的销售总额为17280元．求m的值．

查看试题解析

16. 解不等式组 ${\begin{array}{l} 2 x - 4 < 2 ① \\ 3 x + 2 \geq x ② \end{array}$ 请按下列步骤完成解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集是．

查看试题解析
17. 加强劳动教育，落实五育并举．孝礼中学在当地政府的支持下，建成了一处劳动实践基地.2023年计划将其中 $1000 m^{2}$ 的土地全部种植甲乙两种蔬菜．经调查发现：甲种蔬菜种植成本y（单位；元/ $m^{2}$ ）与其种植面积x（单位： $m^{2}$ ）的函数关系如图所示，其中 $200 \leq x \leq 700$ ；乙种蔬菜的种植成本为50元/ $m^{2}$ ．

(1)、当 $x =$ $m^{2}$ 时， $y = 35$ 元/ $m^{2}$ ；

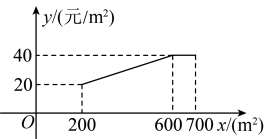(2)、设2023年甲乙两种蔬菜总种植成本为W元，如何分配两种蔬菜的种植面积，使W最小？

(3)、学校计划今后每年在这 $1000 m^{2}$ 土地上，均按（2）中方案种植蔬菜，因技术改进，预计种植成本逐年下降，若甲种蔬菜种植成本平均每年下降 $10 %$ ，乙种蔬菜种植成本平均每年下降 $a %$ ，当a为何值时，2025年的总种植成本为 $28920$ 元？

查看试题解析
18. 创建文明城市，构建美好家园．为提高垃圾分类意识，幸福社区决定采购A，B两种型号的新型垃圾桶．若购买3个A型垃圾桶和4个B型垃圾桶共需要580元，购买6个A型垃圾桶和5个B型垃圾桶共需要860元．

(1)、求两种型号垃圾桶的单价；

(2)、若需购买A，B两种型号的垃圾桶共200个，总费用不超过15000元，至少需购买A型垃圾桶多少个？

查看试题解析
19. 1号探测气球从海拔10m处出发，以1m/min的速度竖直上升．与此同时，2号探测气球从海拔20m处出发，以am/min的速度竖直上升．两个气球都上升了1h.1号、2号气球所在位置的海拔 $y_{1}$ ， $y_{2}$ （单位：m）与上升时间x（单位：min）的函数关系如图所示．请根据图象回答下列问题：

(1)、a= ， b；

(2)、请分别求出 $y_{1}$ ， $y_{2}$ 与x的函数关系式；

(3)、当上升多长时间时，两个气球的海拔竖直高度差为5m？

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - (2 m + 1) x + m^{2} + m = 0$ ．

(1)、求证：无论m取何值时，方程都有两个不相等的实数根；

(2)、设该方程的两个实数根为a，b，若 $(2 a + b) (a + 2 b) = 20$ ，求m的值．

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $k x^{2} - (2 k + 4) x + k - 6 = 0$ 有两个不相等的实数根．

(1)、求 $k$ 的取值范围；

(2)、当 $k = 1$ 时，用配方法解方程．

查看试题解析
22. 荆州古城旁“荆街”某商铺打算购进A，B两种文创饰品对游客销售．已知1400元采购A种的件数是630元采购B种件数的2倍，A种的进价比B种的进价每件多1元，两种饰品的售价均为每件15元；计划采购这两种饰品共600件，采购B种的件数不低于390件，不超过A种件数的4倍．

(1)、求A，B饰品每件的进价分别为多少元？

(2)、若采购这两种饰品只有一种情况可优惠，即一次性采购A种超过150件时，A种超过的部分按进价打6折．设购进A种饰品x件，①求x的取值范围；②设计能让这次采购的饰品获利最大的方案，并求出最大利润．

查看试题解析