浙教版数学八年级下学期第六章 反比例函数 单元测试(培优卷)
试卷更新日期:2024-03-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 已知函数 是反比例函数,则 的值为( )A、2 B、-2 C、2或-2 D、任意实数2. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、3. 用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I2R,下面说法正确的是( )A、P为定值,I与R成反比例 B、P为定值,I2与R成反比例 C、P为定值,I与R成正比例 D、P为定值,I2与R成正比例4. 在同一直角坐标系中,函数与的图象可能是( )A、
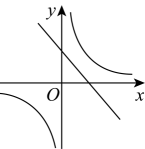 B、
B、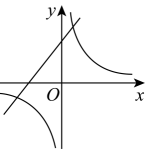 C、
C、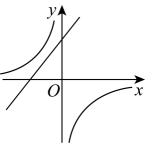 D、
D、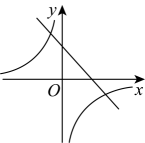 5. 已知反比例函数y=﹣ ,下列结论不正确的是( )A、图象必经过点(﹣1,2) B、y随x的增大而增大 C、图象在第二、四象限内 D、若x>1,则﹣2<y<06. 若点A(x₁,-2),B(x₂,1),C(x₃,2)都在反比例函数的图象上,则x₁,x₂,x₂的大小关系是( )A、 B、 C、 D、7. 如图,正方形ABCD的顶点A,B在y轴上,反比例函数的图象经过点C和AD的中点E,若AB=2,则k的值是( )
5. 已知反比例函数y=﹣ ,下列结论不正确的是( )A、图象必经过点(﹣1,2) B、y随x的增大而增大 C、图象在第二、四象限内 D、若x>1,则﹣2<y<06. 若点A(x₁,-2),B(x₂,1),C(x₃,2)都在反比例函数的图象上,则x₁,x₂,x₂的大小关系是( )A、 B、 C、 D、7. 如图,正方形ABCD的顶点A,B在y轴上,反比例函数的图象经过点C和AD的中点E,若AB=2,则k的值是( )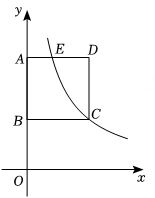 A、3 B、4 C、5 D、68. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( )
A、3 B、4 C、5 D、68. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、49. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( )
A、1 B、 C、2 D、49. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,正方形的顶点 , 分别在轴、轴上,反比例函数( , )的图象与正方形的两边 , 分别交于点 , , 轴,垂足为 , 连接 , , , 下列结论:①;②四边形与的面积相等;③;④若 , , 则点的坐标为 . 其中正确的是( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,正方形的顶点 , 分别在轴、轴上,反比例函数( , )的图象与正方形的两边 , 分别交于点 , , 轴,垂足为 , 连接 , , , 下列结论:①;②四边形与的面积相等;③;④若 , , 则点的坐标为 . 其中正确的是( ) A、①② B、①②④ C、②③④ D、①②③④
A、①② B、①②④ C、②③④ D、①②③④二、填空题(每题4分,共24分)
-
11. 若点在反比例函数图像上,则代数式 .12. 已知 , 那么 .13. 把 化为 的形式为比例系数为自变量 的取值范围是.14. 反比例函数的图象在第一、三象限,则的取值范围是 .15. 若点 , 在反比例函数的图象上,且 , 则m的取值范围是 .16. 将一定体积的面团做成拉面,面条的总长度y(cm)与粗细(横截面面积)x(cm2)之间的函数关系如图所示.如果将这个面团做成粗细为0.16 cm2 的拉面,那么做出来的面条的长度为cm.

三、解答题(共8题,共66分)
-
17. 已知直线与轴、轴交于、两点,是该直线上在第一象限内的一点,轴,为垂足, .
 (1)、求点的坐标;(2)、求过点的反比例函数解析式.18. 某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变实验发现,当每次漂洗用水量v(升)一定时,衣服中残留的洗衣粉量y(克)与漂洗次数x(次)满足y=(k为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.(1)、求k的值.(2)、如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?(3)、现将20升水等分成x次(x>1)漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?19. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长米,另一边长加长米,可得与之间的函数关系式某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数 , 现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整:
(1)、求点的坐标;(2)、求过点的反比例函数解析式.18. 某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变实验发现,当每次漂洗用水量v(升)一定时,衣服中残留的洗衣粉量y(克)与漂洗次数x(次)满足y=(k为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.(1)、求k的值.(2)、如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?(3)、现将20升水等分成x次(x>1)漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?19. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长米,另一边长加长米,可得与之间的函数关系式某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数 , 现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整: (1)、类比反比例函数可知,函数的自变量的取值范围是 , 这个函数值的取值范围是 .(2)、“数学兴趣小组”进一步思考函数的图象和性质,请根据函数的图象,画出函数的图象;(3)、结合函数的图象解答下列问题:
(1)、类比反比例函数可知,函数的自变量的取值范围是 , 这个函数值的取值范围是 .(2)、“数学兴趣小组”进一步思考函数的图象和性质,请根据函数的图象,画出函数的图象;(3)、结合函数的图象解答下列问题:①求出方程的根;
②如果方程有2个实数根,请直接写出的取值范围.
20. 如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于A,BC⊥y轴于C,BA=3,BC=5,有一反比例函数图象刚好过点B.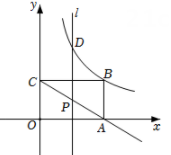 (1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.21. 为预防传染病,某校定期对教室进行“药熏消毒”.已知某种药物在燃烧阶段,室内每立方米空气中的含药量与燃烧时间成正比例;一次性燃烧完以后,y与x成反比例(如图所示).在药物燃烧阶段,实验测得在燃烧5分钟后,此时教室内每立方米空气含药量为 .
(1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.21. 为预防传染病,某校定期对教室进行“药熏消毒”.已知某种药物在燃烧阶段,室内每立方米空气中的含药量与燃烧时间成正比例;一次性燃烧完以后,y与x成反比例(如图所示).在药物燃烧阶段,实验测得在燃烧5分钟后,此时教室内每立方米空气含药量为 . (1)、若一次性燃烧完药物需10分钟.
(1)、若一次性燃烧完药物需10分钟.①分别求出药物燃烧时及一次性燃烧完以后y关于x的函数表达式.
②当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时间段学生不能停留在教室里?
(2)、已知室内每立方米空气中的含药量不低于时,才能有效消毒,如果有效消毒时间要持续120分钟,问要一次性燃烧完这种药物需多长时间?22. 如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=2OB,反比例函数 在第一象限的图象经过正方形的顶点C. (1)、求点C的坐标;(2)、如图2,将正方形ABCD沿x轴向右平移得到正方形 A'B'CD',点 A'恰好落在反比例函数的图象上,求此时点 D'的坐标;(3)、在(2)的条件下,点P为y轴上一动点,平面内是否存在点Q,使以点O、A'、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.23. 如图,已知A(-3,2),B(n , -3)是一次函数y=kx+b的图象与反比例函数的图象的两个交点.
(1)、求点C的坐标;(2)、如图2,将正方形ABCD沿x轴向右平移得到正方形 A'B'CD',点 A'恰好落在反比例函数的图象上,求此时点 D'的坐标;(3)、在(2)的条件下,点P为y轴上一动点,平面内是否存在点Q,使以点O、A'、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.23. 如图,已知A(-3,2),B(n , -3)是一次函数y=kx+b的图象与反比例函数的图象的两个交点. (1)、求反比例函数和一次函数的解析式;(2)、根据图象写出使一次函数的值大于反比例函数的值的x的取值范围;(3)、求△AOB的面积;(4)、在x轴上是否存在一点P , 使△AOP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.24. 根据以下素材,探索完成任务.
(1)、求反比例函数和一次函数的解析式;(2)、根据图象写出使一次函数的值大于反比例函数的值的x的取值范围;(3)、求△AOB的面积;(4)、在x轴上是否存在一点P , 使△AOP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.24. 根据以下素材,探索完成任务.制作检测酒精的漂浮吸管
素材1
如图1,装有钢珠且下端密封的吸管漂浮在液体中时,所受重力与浮力大小相等,吸管浸在液体中的深度会因液体密度的改变而改变.

素材2
小明通过观察与测量,得到漂浮在液体中吸管的示数与液体密度ρ()之间的几组数据如下表:
h(cm)
…
…
ρ()
…
…
素材3
浓度为a%的酒精密度(酒精与水的密度分别为 , ):
问题解决
任务1
求ρ关于h的函数表达式.
任务2
由吸管上对应的刻度线可判断配置的酒精浓度.图2已标出吸管在水中的位置,请通过计算,标出可以检测75%酒精的吸管位置.(精确到)
