2024年浙教版数学八年级下学期第六章反比例函数单元测试（基础卷）

试卷更新日期：2024-03-06 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列关系式中， $y$ 是 $x$ 的反比例函数的是（）

A、 $y = \frac{x}{3}$ B、 $y = x^{2}$ C、 $y = - \frac{3}{x}$ D、 $y = \frac{1}{x^{2}}$

查看试题解析
2. 若反比例函数 $y = \frac{2}{x}$ 中， $x$ 与 $y$ 的值相等，则这个相等的值为（）

A、2 B、 $\pm \sqrt{2}$ C、 $\sqrt{2}$ D、 $- \sqrt{2}$

查看试题解析
3. 已知蓄电池两端电压 $U$ 为定值，电流 $I$ 与 $R$ 的函数关系为 $I = \frac{U}{R} .$ 当 $I = 3 A$ 时， $R = 8 Ω$ ，则当 $I = 6 A$ 时， $R$ 的值为（）

A、 $4 Ω$ B、 $6 Ω$ C、 $8 Ω$ D、 $10 Ω$

查看试题解析
4. 在反比例函数 $y = \frac{m - 1}{x}$ 中， $m$ 的取值范围是（ )

A、 $m \neq 1$ B、 $m > 1$ C、 $m > 0$ D、 $m \neq 0$

查看试题解析
5. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $P (3 ， 2)$ ，则k的值为（）

A、3 B、4 C、5 D、6

查看试题解析
6. 在双曲线 $y = \frac{1 - k}{x}$ 的每一支上，y随x的增大而增大，则k的值可以是（）

A、2 B、0 C、-2 D、1

查看试题解析
7. 反比例函数 $y = - \frac{4}{x}$ 的图象一定经过的点是（）

A、(1，4) B、(-1，-4) C、(-2，2) D、(2，2)

查看试题解析
8. 已知近视眼镜的度数y（度）与镜片焦距x（米）之间成反比例函数关系，如图所示，则眼镜度数y与镜片焦距x之间的函数关系式是（　　）

A、 $y = 100 x$ B、 $y = 200 x$ C、 $y = \frac{100}{x}$ D、 $y = \frac{200}{x}$

查看试题解析
9. 函数 $y = \frac{1}{2 x}$ 中自变量的取值范围是（）

A、 $x \geq 0$ B、 $x \neq 0$ C、 $x \leq 0$ D、 $x > 0$

查看试题解析
10. 反比例函数 $y = \frac{k}{x} (x > 0)$ 图像上有两个点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ， $(x_{1} - x_{2}) (y_{1} - y_{2}) < 0$ ，则 $y = k x - k$ 的图像不经过第（）象限

A、一 B、二 C、三 D、四

查看试题解析

二、填空题（每题4分，共24分）

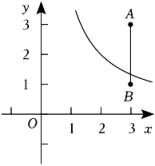
11. 下列关系式：①y= $\frac{x}{3}$ ；②y= $- \frac{6}{7 x}$ ；③xy=-1；④y= $\frac{5}{x + 1}$ ；⑤y=2x^-1 ．其中y是x的反比例函数的为． (只填序号)

查看试题解析
12. $y = (m - 2) x^{m^{2} - 5}$ 是反比例函数，则 $m$ 的值为．

查看试题解析
13. 如图，已知点A（3，3），B（3，1），反比例函数 $y = \frac{k}{x} (k \neq 0)$ 图象的一支与线段AB有交点，写出一个符合条件的k的整数值：．

查看试题解析
14. 若在反比例函数 $y = \frac{m - 2}{x}$ 的图象的每一条曲线上，y都随x的增大而减小，则m的取值范围是

查看试题解析
15. 反比例函数 $y = \frac{m - 3}{x}$ 的图象在二、四象限，则 $m$ 应满足．

查看试题解析
16. 科技小组为了验证某电路的电压U（V）、电流I（A）、电阻 $R (Ω)$ 三者之间的关系： $I = \frac{U}{R}$ ，测得数据如下：

$R (Ω)$

100

200

220

400

$I (A)$

2.2

1.1

1

0.55

那么，当电阻 $R = 55 Ω$ 时，电流 $I =$ A.

查看试题解析

三、解答题（共8题，共66分）

17. 已知y=y₁+y₂ ， y₁与x成正比例，y₂与x+2成反比例，且当x=﹣1时，y=3；当x=3时，y=7．求x=﹣3时，y的值．

查看试题解析
18. 已知反比例函数的解析式 $y = \frac{k}{x}$ ，并且当x=3时，y=4．

(1)、求反比例函数的解析式；

(2)、当x=－2时，求y的值。

查看试题解析
19. 已知反比例函数y= $\frac{n + 6}{x}$ 的图象经过第二、四象限，求n的取值范围．

查看试题解析
20. 如图，根据小孔成像的科学原理，当像距 $($ 小孔到像的距离 $)$ 和物高 $($ 蜡烛火焰高度 $)$ 不变时，火焰的像高 $y ($ 单位： $c m)$ 是物距 $($ 小孔到蜡烛的距离 $) x ($ 单位： $c m)$ 的反比例函数，当 $x = 6$ 时， $y = 2$ ．

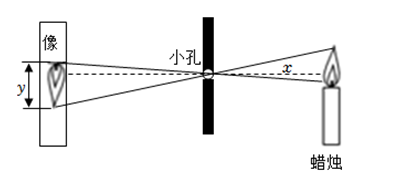(1)、求 $y$ 关于 $x$ 的函数解析式．

(2)、若火焰的像高为 $3 c m$ ，求小孔到蜡烛的距离．

查看试题解析
21. 已知函数 $y = (5 m - 3) x^{2 - n} + (n + m)$ ，

(1)、当 $m$ ， $n$ 为何值时是一次函数？

(2)、当 $m$ ， $n$ 为何值时，为正比例函数？

(3)、当 $m$ ， $n$ 为何值时，为反比例函数？

查看试题解析
22. 如图，一次函数y=kx+b的图象与反比例函数 $y = \frac{4}{x}$ 的图象相交于点A(m，4)，与x轴相交于点B，与y轴相交于点C(0，3).

(1)、求m的值和一次函数的表达式.

(2)、已知P为反比例函数： $y = \frac{4}{x}$ 图象上的一点， $S_{△ O B P} = 2 S_{△ a v c}$ ，求点P的坐标.

查看试题解析
23. 如图，已知一次函数y=2x+b的图象与反比例函数 $y = \frac{m}{x}$ 的图象相交于A，B两点，与y轴相交于点C，且点B的坐标为(-3，-1).

(1)、求一次函数和反比例函数的表达式及点A的坐标.

(2)、若 $2 x + b < \frac{m}{x} ，$ 请直接写出x的取值范围.

(3)、求△AOB的面积.

查看试题解析
24. 如图，在平面直角坐标系中，点 B在第一象限，BA⊥x轴于点A，BC⊥y轴于点C，BA=3，BC=5，有一反比例函数的图象刚好经过点 B.

(1)、分别求出该反比例函数的表达式和直线 AC 的函数表达式.

(2)、动点P 在射线CA(不与点C重合)上，过点 P 作直线l⊥x轴，交反比例函数图象于点 D.在坐标平面内，是否存在这样的点Q，使得以点 B，D，P，Q为顶点的四边形为菱形? 若存在，求出点 Q 的坐标；若不存在，请说明理由.

查看试题解析

$R (Ω)$	100	200	220	400
$I (A)$	2.2	1.1	1	0.55

2024年浙教版数学八年级下学期第六章 反比例函数 单元测试（基础卷）

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2024年浙教版数学八年级下学期第六章反比例函数单元测试（基础卷）