浙教版数学八年级下学期第五章 特殊平行四边形 单元测试(培优卷)
试卷更新日期:2024-03-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD 于点E,F,则阴影部分的面积是矩形ABCD 面积的 ( )
 A、 B、 C、 D、2. 下列说法中,错误的是( )A、有一个角是直角的四边形是矩形 B、四个角都相等的四边形是矩形 C、对角线相等的平行四边形是矩形 D、对角线互相平分且相等的四边形是矩形3. 如图,菱形ABCD的两条对角线交于点O,BE⊥DC,交DC的延长线于点E,若AC=6, BD=8,则BE的长是( )
A、 B、 C、 D、2. 下列说法中,错误的是( )A、有一个角是直角的四边形是矩形 B、四个角都相等的四边形是矩形 C、对角线相等的平行四边形是矩形 D、对角线互相平分且相等的四边形是矩形3. 如图,菱形ABCD的两条对角线交于点O,BE⊥DC,交DC的延长线于点E,若AC=6, BD=8,则BE的长是( ) A、 B、 C、 D、44. 如图,将△ABC沿BC方向平移得到△DCE,连结BD,AD,下列条件不能判定四边形ABCD是菱形的是( )
A、 B、 C、 D、44. 如图,将△ABC沿BC方向平移得到△DCE,连结BD,AD,下列条件不能判定四边形ABCD是菱形的是( )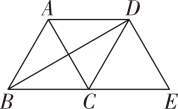 A、∠ABC=∠ACB B、AB=AD C、∠BAC=∠DAC D、AC⊥BD5. 已知,O是矩形ABCD 对角线的交点,作 DE∥AC,AE∥BD,连结BE.有下列说法:①四边形DEAO为菱形;②AE=AB;③∠BAE=120°;④若∠BED=90°,则AD=BE.其中正确的是 ( )
A、∠ABC=∠ACB B、AB=AD C、∠BAC=∠DAC D、AC⊥BD5. 已知,O是矩形ABCD 对角线的交点,作 DE∥AC,AE∥BD,连结BE.有下列说法:①四边形DEAO为菱形;②AE=AB;③∠BAE=120°;④若∠BED=90°,则AD=BE.其中正确的是 ( )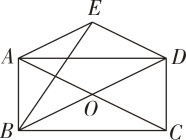 A、①③ B、①④ C、②④ D、③④6. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( )
A、①③ B、①④ C、②④ D、③④6. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( ) A、1 B、 C、 D、7. 如图,在边长为4的正方形ABCD中,∠CDE=30°,DE⊥CF,则AF 的长为 ( )
A、1 B、 C、 D、7. 如图,在边长为4的正方形ABCD中,∠CDE=30°,DE⊥CF,则AF 的长为 ( )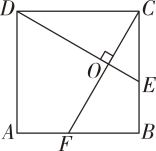 A、 B、 C、 D、8. 如图,在△ABC中,点D,E,F分别在边BC,AB,CA 上,且 DE∥CA,DF∥BA.有下列说法:
A、 B、 C、 D、8. 如图,在△ABC中,点D,E,F分别在边BC,AB,CA 上,且 DE∥CA,DF∥BA.有下列说法: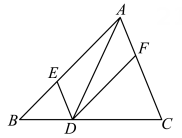
①四边形AEDF 是平行四边形;
②若∠BAC=90°,则四边形AEDF 是矩形;
③若 AD平分∠BAC,则四边形AEDF 是菱形;
④若AD⊥BC,且AB=AC,则四边形AEDF 是正方形.
其中正确的是 ( )
A、①④ B、②③ C、①②③ D、①②③④9. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )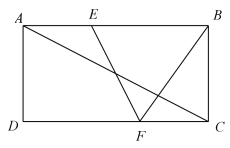 A、 B、 C、4 D、610. 如图,在 Rt△ABC中,LACB=90°,以其三边为边在AB的同侧作三个正方形,点F在GH 上,CG与EF相交于点P,CM 与BE相交于点Q.若HF=FG则的值是( )
A、 B、 C、4 D、610. 如图,在 Rt△ABC中,LACB=90°,以其三边为边在AB的同侧作三个正方形,点F在GH 上,CG与EF相交于点P,CM 与BE相交于点Q.若HF=FG则的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 如图,在矩形ABCD中,E是边AD 上一点,F 是边AB 上一点,EF=CE,且EF⊥CE,连结CF.若 DE= 2cm ,矩形 ABCD的周长为16 cm,求 AE 及 CF 的长.
 12. 如图,在矩形ABCD中,对角线 AC,BD相交于点O,E 是边AD 的中点,点 F 在对角线AC 上,且AF=AC,连结 EF.若AC=10,则EF .
12. 如图,在矩形ABCD中,对角线 AC,BD相交于点O,E 是边AD 的中点,点 F 在对角线AC 上,且AF=AC,连结 EF.若AC=10,则EF . 13. 如图,有两张矩形纸片 ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.将两纸片按如图所示的方式叠放,使点D 与点G 重合,且重叠部分为▱MNDK.若两张纸片交叉所成的角记为α,则当a=30°时,BM=cm;当α最小时,重叠部分的面积为cm2.
13. 如图,有两张矩形纸片 ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.将两纸片按如图所示的方式叠放,使点D 与点G 重合,且重叠部分为▱MNDK.若两张纸片交叉所成的角记为α,则当a=30°时,BM=cm;当α最小时,重叠部分的面积为cm2.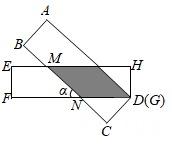 14. 如图,在菱形ABCD中,E是边CD上一点,连结AE 交对角线 BD 于点F,连结CF.若∠AED=40°,则∠BCF的度数为°.
14. 如图,在菱形ABCD中,E是边CD上一点,连结AE 交对角线 BD 于点F,连结CF.若∠AED=40°,则∠BCF的度数为°.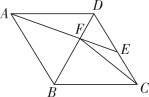 15. 正方形和正方形中,点在上, , , 是的中点,那么的长是 .
15. 正方形和正方形中,点在上, , , 是的中点,那么的长是 . 16. 四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF.
16. 四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF.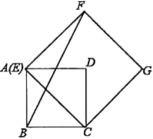
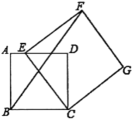
图1 图2
(1)、如图1,当点E与点A重合时,;(2)、如图2,当点E在线段AD上时, , 则 .三、解答题(共8题,共66分)
-
17. 如图,在△ABC 中,AB=AC,D,E 分别是线段 BC,AD的中点,过点 A 作 BC 的平行线交BE 的延长线于点 F,连结 CF.求证:
 (1)、△BDE≌△FAE.(2)、四边形 ADCF 是矩形.18. 如图,点是一次函数图象上一点.过点分别作轴,轴的垂线段,垂足为点A,B.
(1)、△BDE≌△FAE.(2)、四边形 ADCF 是矩形.18. 如图,点是一次函数图象上一点.过点分别作轴,轴的垂线段,垂足为点A,B. (1)、矩形OAPB的周长是否为定值?若是请求出此定值,若不是,请说明理由;(2)、连接的周长是否为定值?若是请求出此定值,如不是,请求出其最小值.19. 如图,菱形ABCD的对角线相交于点O,BE∥AC,AE∥BD,EO与AB相交于点F.
(1)、矩形OAPB的周长是否为定值?若是请求出此定值,若不是,请说明理由;(2)、连接的周长是否为定值?若是请求出此定值,如不是,请求出其最小值.19. 如图,菱形ABCD的对角线相交于点O,BE∥AC,AE∥BD,EO与AB相交于点F.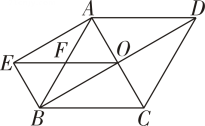 (1)、求证:EO=DC;(2)、若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.20. 如图,在△ABF中,∠A=90°,AB=2,AF=3,E 是边 BF 的中点,D是边 AF 上一点,连结DE 并延长至点C,使得CE=DE.
(1)、求证:EO=DC;(2)、若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.20. 如图,在△ABF中,∠A=90°,AB=2,AF=3,E 是边 BF 的中点,D是边 AF 上一点,连结DE 并延长至点C,使得CE=DE. (1)、求证:四边形 BDFC 是平行四边形.(2)、若CD⊥BF,求CD长.21. 如图,在△ABC中,AB=AC,AD是BC 边上的中线,E 是 AD 上一点,过点 B作BF∥EC,交AD的延长线于点F,连结BE,CF.
(1)、求证:四边形 BDFC 是平行四边形.(2)、若CD⊥BF,求CD长.21. 如图,在△ABC中,AB=AC,AD是BC 边上的中线,E 是 AD 上一点,过点 B作BF∥EC,交AD的延长线于点F,连结BE,CF.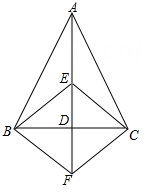 (1)、求证:△BDF≌△CDE.(2)、当 ED 与BC 满足什么数量关系时,四边形BECF 是正方形? 请说明理由.22. 如图1,矩形ABCD中,过对角线AC的中点O画EF⊥AC分别交AB,CD于点E,F,连结AF,CE.
(1)、求证:△BDF≌△CDE.(2)、当 ED 与BC 满足什么数量关系时,四边形BECF 是正方形? 请说明理由.22. 如图1,矩形ABCD中,过对角线AC的中点O画EF⊥AC分别交AB,CD于点E,F,连结AF,CE.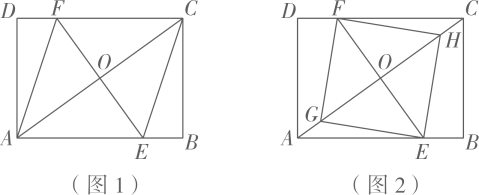 (1)、[证明体验]
(1)、[证明体验]求证:四边形AECF是菱形.
(2)、[基础巩固]若AB=8,BC=6,求菱形AECF的边长.
(3)、[拓展延伸]如图2,在对角线AC上取点G,H,使得四边形EHFG是正方形,若正方形EHFG的边长为 , 且AE=5CH,求矩形ABCD的面积.
23. 如图,四边形 ABCD为正方形,E 为对角线AC 上一点,连结 DE,过点 E 作EF⊥DE,交BC于点 F,以DE,EF为邻边作矩形 DEFG,连结 CG. (1)、求证:矩形 DEFG 是正方形.(2)、若 求 CG 的长.(3)、当 时,求∠EFC的度数.24. 【定义】对于没有公共点的两个图形 , , 点是图形上任意一点,点是图形上任意一点,把、两点之间的距离的最小值称为图形与图形的距离,记为 .
(1)、求证:矩形 DEFG 是正方形.(2)、若 求 CG 的长.(3)、当 时,求∠EFC的度数.24. 【定义】对于没有公共点的两个图形 , , 点是图形上任意一点,点是图形上任意一点,把、两点之间的距离的最小值称为图形与图形的距离,记为 .
【理解】如图1,在平面直角坐标系中,的对角线 , 相交于点 , 若点 , 的坐标分别为 , , 点是边上任意一点.
(1)、当点在边上时,的最小值是 , 因此[点 , 线段]=;(2)、当点在任意边上时,的最小值是 , 因此[点 , ]=;(3)、【拓展】如图2,在平面直角坐标系中,的对角线 , 相交于点 , 平分 , 点 , 的坐标分别为 , , 点是对角线上与点 , , 不重合的一点,点是对角线上与点 , , 不重合的一点.
当[线段 , ]时,则的取值范围为;(4)、当时,(结果用含的式子表示);(5)、【应用】为庆祝母亲节,某商场在广场举行花卉展览,要在长6米,宽4米的长方形花卉展览区外围用彩绳拉出封闭隔离线,要求封闭隔离线与长方形花卉展览区外围的最小距离均为米,请直接写出所需彩绳的长度.