浙教版数学八年级下学期第五章 特殊平行四边形 单元测试(基础卷)
试卷更新日期:2024-03-06 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,四边形ABCD是平行四边形,下列说法不正确的是( )
 A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC平分∠BAD时,四边形ABCD是菱形 D、当∠DAB= 90°时,四边形ABCD是正方形2. 黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形的底边取中点E , 以E为圆心,线段为半径作圆,其与底边的延长线交于点F , 这样就把正方形延伸为矩形 , 称其为黄金矩形.若 , 则( ).
A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC平分∠BAD时,四边形ABCD是菱形 D、当∠DAB= 90°时,四边形ABCD是正方形2. 黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形的底边取中点E , 以E为圆心,线段为半径作圆,其与底边的延长线交于点F , 这样就把正方形延伸为矩形 , 称其为黄金矩形.若 , 则( ).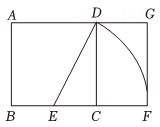 A、 B、 C、 D、3. 已知四边形 ABCD 是平行四边形,有下列条件:①AB=BC;②∠ABC=90°;③∠ABD=∠CBD;④AC⊥BD. 从中选一个条件作为补充,能使□ABCD变为菱形的是 ( )A、① B、①③ C、②④ D、①③④4. 如图,四边形 ABCD的对角线互相平分,要使它变为菱形,还需要添加的条件是( )
A、 B、 C、 D、3. 已知四边形 ABCD 是平行四边形,有下列条件:①AB=BC;②∠ABC=90°;③∠ABD=∠CBD;④AC⊥BD. 从中选一个条件作为补充,能使□ABCD变为菱形的是 ( )A、① B、①③ C、②④ D、①③④4. 如图,四边形 ABCD的对角线互相平分,要使它变为菱形,还需要添加的条件是( )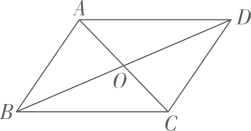 A、AB=CD B、AD=BC C、AC=BD D、AB=BC5. 如图,在矩形ABCD中,AD>AB,点E,F分别在边AD,BC上,EF∥AB,AE=AB,AF与BE相交于点O,连结OC.若BF=2CF,则OC与EF之间的数量关系正确的是( )
A、AB=CD B、AD=BC C、AC=BD D、AB=BC5. 如图,在矩形ABCD中,AD>AB,点E,F分别在边AD,BC上,EF∥AB,AE=AB,AF与BE相交于点O,连结OC.若BF=2CF,则OC与EF之间的数量关系正确的是( ) A、 B、 C、 D、OC=EF6. 小颖用4张长为a、宽为b的长方形纸片,按如图所示的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1 , 阴影部分的面积为S2.若a=2b,则S1 , S2之间的数量关系为( )
A、 B、 C、 D、OC=EF6. 小颖用4张长为a、宽为b的长方形纸片,按如图所示的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1 , 阴影部分的面积为S2.若a=2b,则S1 , S2之间的数量关系为( ) A、 B、 C、 D、7. 如图,在矩形中,分别是上的点,分别是的中点. , , 则线段的长为( )
A、 B、 C、 D、7. 如图,在矩形中,分别是上的点,分别是的中点. , , 则线段的长为( ) A、6 B、6.5 C、7 D、58. 菱形的对角线 , 则菱形的面积是( )A、20 B、15 C、12 D、109. 如图,从边长为的正方形纸片中剪去一个边长为的正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则拼成的矩形的面积是( ).
A、6 B、6.5 C、7 D、58. 菱形的对角线 , 则菱形的面积是( )A、20 B、15 C、12 D、109. 如图,从边长为的正方形纸片中剪去一个边长为的正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则拼成的矩形的面积是( ).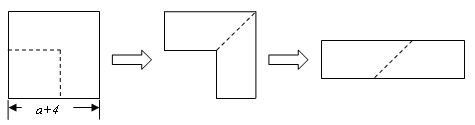 A、 B、 C、 D、10. 如图,正方形ABCD的边长为 10,AG=CH=8,BG=DH=6,连结GH,则GH 的长为 ( )
A、 B、 C、 D、10. 如图,正方形ABCD的边长为 10,AG=CH=8,BG=DH=6,连结GH,则GH 的长为 ( )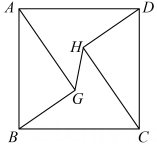 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题(每题4分,共24分)
-
11. 已知黄金矩形的宽为﹣2,则这个黄金矩形的面积是 . (注:宽∶长=的矩形为黄金矩形)12. 一个长方形的宽为x厘米,长比宽的2倍多3厘米,则此长方形的周长为厘米。13. 如图,在菱形ABCD中,若AC=12,BD=9,则菱形ABCD的面积是.
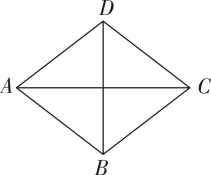 14. 如图,菱形ABCD的周长16cm,则菱形ABCD的一边中点E到对角线交点O的距离为.cm.
14. 如图,菱形ABCD的周长16cm,则菱形ABCD的一边中点E到对角线交点O的距离为.cm.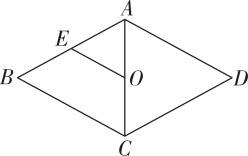 15. 如图,A(0,2),D(1,0),以AD为边作正方形ABCD , 则点B的坐标为 .
15. 如图,A(0,2),D(1,0),以AD为边作正方形ABCD , 则点B的坐标为 . 16. 如图,是正方形内的一点,连结、 , 将绕点逆时针旋转到的位置,则它旋转了 度.
16. 如图,是正方形内的一点,连结、 , 将绕点逆时针旋转到的位置,则它旋转了 度.
三、解答题(共8题,共66分)
-
17. 如图,在 中, 于E,点F在边 上, ,求证:四边形 是矩形.
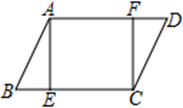 18. 已知:如图,点F在ABC的边AC上,过点F、B分别作AB、AC的平行线相交于点E , 连接BF , AB=AF . 求证:四边形ABEF是菱形.
18. 已知:如图,点F在ABC的边AC上,过点F、B分别作AB、AC的平行线相交于点E , 连接BF , AB=AF . 求证:四边形ABEF是菱形. 19. 如图,矩形 的对角线 , 相交于点O,且 .求证:四边形 是菱形.
19. 如图,矩形 的对角线 , 相交于点O,且 .求证:四边形 是菱形. 20. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.
20. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF,求证:△ABE≌△BCF.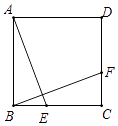 21. 已知:如图,E,F是正方形的对角线上的两点,且 . 求证:四边形是菱形.
21. 已知:如图,E,F是正方形的对角线上的两点,且 . 求证:四边形是菱形.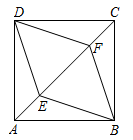 22. 如图,正方形ABCD 的对角线AC,BD相交于点O,E是OC 上一点,OE=2,连结 EB.过点 A 作AM⊥BE,垂足为 M,AM 与BD 相交于点 F.求OF 的长.
22. 如图,正方形ABCD 的对角线AC,BD相交于点O,E是OC 上一点,OE=2,连结 EB.过点 A 作AM⊥BE,垂足为 M,AM 与BD 相交于点 F.求OF 的长. 23. 如图,在平行四边形中,对角线与相交于点 , 点 , 分别为 , 的中点,延长至 , 使 , 连接 .
23. 如图,在平行四边形中,对角线与相交于点 , 点 , 分别为 , 的中点,延长至 , 使 , 连接 . (1)、求证:≌;(2)、当线段与线段满足什么数量关系时,四边形是矩形?请说明理由.24. [推理能力]如图,在□ABCD中,AB=2cm,AC=5cm ,S▱ABCD =8 cm²,点 E 从点 B 出发,以1cm/s的速度在 AB 的延长线上向右运动,同时点 F 从点 D 出发,以同样的速度在 CD的延长线上向左运动,运动时间为t(s).
(1)、求证:≌;(2)、当线段与线段满足什么数量关系时,四边形是矩形?请说明理由.24. [推理能力]如图,在□ABCD中,AB=2cm,AC=5cm ,S▱ABCD =8 cm²,点 E 从点 B 出发,以1cm/s的速度在 AB 的延长线上向右运动,同时点 F 从点 D 出发,以同样的速度在 CD的延长线上向左运动,运动时间为t(s). (1)、在运动过程中,四边形 AECF 的形状是 .(2)、当t=时,四边形 AECF 是矩形.(3)、当 t 的值为多少时,四边形 AECF 是菱形?
(1)、在运动过程中,四边形 AECF 的形状是 .(2)、当t=时,四边形 AECF 是矩形.(3)、当 t 的值为多少时,四边形 AECF 是菱形?