2024年浙教版数学八年级下学期第四章 平行四边形单元测试（基础卷）
试卷更新日期：2024-03-06 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 若一个多边形的每一个外角都是36°，则该多边形的边数为（ ）A、7 B、8 C、9 D、102. 小丽利用最近学习的数学知识，给同伴出了这样一道题：如图，小刚从点 A 出发，沿直线走 6米后向左转θ，接着沿直线前进 6 米后，再向左转θ……如此下去，当他第一次回到点A时，发现自己走了 72米，则θ的度数为（ ）
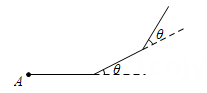A、28° B、30° C、33° D、36°3. 如图，□ABCD的两条对角线相交于点O.若AC=4，BD=5，BC=3，则△BOC的周长为（ ）
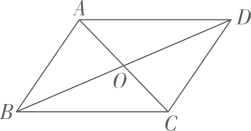A、6 B、7.5 C、9 D、124. 如图，在中， ， 则（ ）
A、30° B、50° C、60° D、120°5. 下列与杭州亚运会有关的图案中，中心对称图形是（ ）A、
B、
C、
D、
6. 如图，在四边形 ABCD中，对角线 AC 和 BD 相交于点O.下列条件中，不能判定四边形ABCD为平行四边形的是 （ ）
A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AB∥DC，AD=BC D、OA=OC，OB=O7. 如图，D，E分别是△ABC的边BA，BC的中点.若AC=3，则 DE 的长为 （ ）
A、2 B、 C、3 D、8. 如图，在△ABC 中，BC=4，D，E分别为AB，AC的中点，则 DE的长为（ ）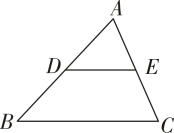
A、 B、 C、1 D、29. 用反证法证明“四边形中至少有一个角是钝角或直角”，可假设四边形的四个角都是（ ）A、钝角或直角 B、钝角 C、直角 D、锐角10. 在中，点D，E分别是 ， 上的点，且 ， 点F是延长线上一点，连接 ． 添加下列条件后，不能判断四边形是平行四边形的是（ ）
A、 B、 C、 D、二、填空题（每题4分，共24分）
-
11. 若从一个多边形的顶点出发可引出6条对角线，则这个多边形共有条对角线.12. 如图，在▱ABCD中，E，F分别在边 BC，AD 上，有以下条件：①AF=CF；②AE=CF；③∠BEA =∠FCE.若要使四边形AFCE 为平行四边形，则还需添加上述条件中的(填序号).
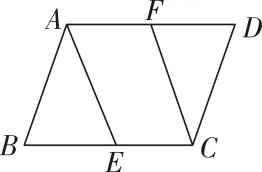13. 如图，在中，、分别是、的中点， ， 则长为 ．
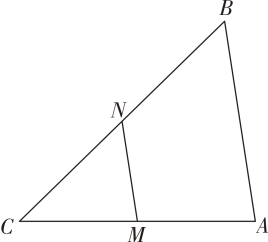14. 已知五个正数的和等于5，用反证法证明这五个数中至少有一个大于或等于1，其中，第一步应假设.15. 用反证法证明，“在△ABC中，∠A、∠B对边是a、b，若∠A>∠B，则a>b．"第一步应假设16. 如图，在菱形中，线段在对角线上运动， ， ， ， 则周长的最小值为 ．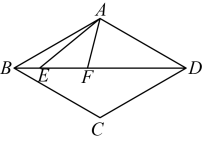
三、解答题（共8题，共66分）
-
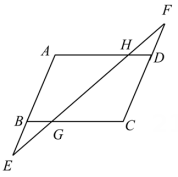
17. 如图，在▱ABCD中，点E在AB的延长线上，点F在CD的延长线上，且满足BE=DF.连结EF，分别与BC，AD相交于点G，H.求证：EG=FH.
18. 如图，E，F分别是▱ABCD的边AB，CD上的点，且AE=CF.求证：DE=BF.
19. 如图，在平行四边形中，点、分别在、延长线上，且求证：四边形为平行四边形．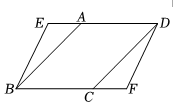
20. 在四边形ABCD中，对角线AC、BD交于点O，若AD=12，OD=OB=5，AC=26，∠ADB=90º，求证：四边形ABCD为平行四边形.
21. 如图，在四边形中，、、分别是、、的中点， ． 求证： ．
