2024年浙教版数学八年级下学期第三章 数据分析初步 单元测试（基础卷）
试卷更新日期：2024-03-05 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 数据-1，0，3，4，4的平均数是（ ）A、4 B、3 C、2.5 D、22. 某校在计算学生的数学学期总评成绩时，规定期中考试成绩占40%，期末考试成绩占60%.如果小林同学的数学期中考试成绩为80分，期末考试成绩为90分，那么他的数学学期总评成绩是（ ）A、8 0分 B、82分 C、84分 D、86分3. 李老师参加本校青年数学教师优质课比赛，笔试得 90分，微型课得 92分，教学反思得 88 分.若分别按照如图所示的权重计算综合成绩，则李老师的综合成绩为 （ ）
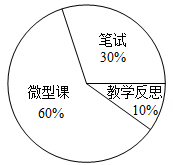A、88分 B、90分 C、91分 D、92分4. 菲尔兹奖是国际上享有崇高声誉的一个数学奖项，每四年评选一次，主要授予年轻的数学家.下面的数据是部分获奖者获奖时的年龄(单位：岁)：29，32，33，35，35，40，则这组数据的众数和中位数分别是（ ）A、35，35 B、34，33 C、34，35 D、35，345. 小楠所在社会实践活动小组的同学们响应“垃圾分类，从我做起”的号召，主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示，那么这组数据的众数和中位数分别是（ ）
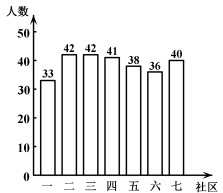A、42，40 B、42，38 C、2，40 D、2，386. 下表是浙江省七个城市某季度 GDP(地区生产总值)数据的情况：城市
嘉兴
绍兴
温州
衢州
杭州
宁波
台州
GDP(亿元)
1517
1610
1889
437
4539
3516
1375
则这组数据的中位数是 （ ）
A、1 889 亿元 B、1610 亿元 C、1517 亿元 D、437亿元7. 甲、乙两人各射击5次，成绩如下表.根据数据分析，在两人的这5次成绩中 （ ）成绩(单位：环)
甲
3
7
8
8
10
乙
7
7
8
9
10
A、甲的平均数大于乙的平均数 B、甲的中位数小于乙的中位数 C、甲的众数大于乙的众数 D、甲的方差小于乙的方差8. 方差是刻画数据波动程度的量，对于一组数据x1 ， x2 ， x3 ， …，xn ， 可用如下算式计算方差： S²= ， 其中“5”是这组数据的 （ ）A、最小值 B、平均数 C、中位数 D、和9. 已知一组数据2，5，4，x，3的平均数是4，则这组数据的标准差是（ ）A、4 B、2 C、 D、10. 有下列说法：①数据7，7，6，5，4的众数是2；②若数据的平均数是 ， 则③数据1，2，3，4，5，6的中位数是3和4；④数据21，22，23，24，25的方差是2.其中正确的是（ ）A、①③ B、②④ C、①②④ D、②③④二、填空题（每题4分，共24分）
-
11. 学校要从王静、李玉两同学中选拔1人参加运动会志愿者工作，选拔项目为普通话、体育知识和旅游知识，并将成绩依次按4：3：3记分.两人的各项选拔成绩如表所示，则最终胜出的同学是.
普通话
体育知识
旅游知识
王静
80
90
70
李玉
90
80
70
12. 学校进行广播操比赛，20 位评委给某班的评分情况统计图如图所示，则该班的平均分是分.广播操比赛某班评分情况统计图
13. 为了落实“双减”政策，增强学生体质，阳光学校篮球兴趣小组开展投篮比赛活动，6名选手投中篮圈的个数分别为2，3，3，4，3，5，则这组数据的众数是.14. 在某中学的一次田径运动会上，参加女子跳高的7名运动员的成绩如下(单位：m)：1.20，1.25，1.10，1.15，1.35，1.30，1.30，则这组数据的中位数是.15. 若一组数据 1，2，3，x的平均数是2，则这组数据的方差是 ．16. 一组数据：2.2，3.3，4.4，11.1，a，其中整数a是这组数据的中位数，则这组数据的平均数是.三、解答题（共8题，共66分）
-
17. 某校学生会要在甲、乙两位候选人中选择一 人担任文艺部干事，对他们进行了文化水平艺术水平组织能力的测试，根据综合成绩择优录取，他们的各项成绩(单项满分100分)如下表所示：
候选人
文化水平
艺术水平
组织能力
甲
80分
87分
82分
乙
80分
96分
76分
(1)、如果把各项成绩的平均数作为综合成绩，应该录取谁？(2)、如果想录取一名组织能力较强的候选人，把文化水平、艺术水平、组织能力三项成绩分别按照20%，20%，60%的比例计人综合成绩，应该录取谁？18. 某中学为加强学生的劳动教育，需要制定学生每周劳动时间(单位：时)的合格标准，为此随机调查了 100 名学生目前每周劳动时间，获得数据并整理成下表.每周劳动时间x(时) 0.5≤x<1.5 1.5≤x<2.5 2.5≤x<3.5 3.5≤x<4.5 4.5≤x<5.5 组中值 1 2 3 4 5 人数 21 30 19 18 12 (1)、画扇形图描述数据时，1.5≤x<2.5这组数据对应的扇形的圆心角是多少度?(2)、估计该校学生目前每周劳动时间的平均数.(3)、请你为该校制定一个学生每周劳动时间的合格标准(时间取整数小时)，并用统计量说明其合理性.19. 小宇观看亚运会跳水比赛，对运动员每一跳成绩的计算方法产生了浓厚的兴趣，查阅资料后，小宇了解到跳水比赛的计分规则为：(a)每次试跳的动作，按照其完成难度的不同，对应一个难度系数 H；
(b)每次试跳都有7 名裁判进行打分(0~10分，分数为0.5的整数倍)，在7个得分中去掉2个最高分和2个最低分，剩下 3个得分的平均值为这次试跳的完成分 P；
(c)运动员该次试跳的得分A=难度系数 H×完成分 P×3.
在比赛中，甲运动员最后一次试跳后的打分如下表所示：
难度系数
裁判
1#
2#
3#
4#
5#
6#
7#
3.5
打分
7.5
8.5
4.0
9.0
8.0
8.5
7.0
(1)、甲运动员这次试跳的完成分 P甲= ， 得分A甲=.(2)、如果按照全部7 名裁判打分的平均分来计算完成分，得到的完成分为 P甲'，那么与(1)中所得的P甲比较， P甲'P甲(填“>”“<”或 “= ”).(3)、在最后一次试跳之前，乙运动员的总分比甲运动员低13.1分，已知乙最后一次试跳的难度系数为3.6，若乙想要在总分上反超甲，则这一跳乙的完成分 P乙至少要达到多少分?20. 某校为响应“传承楚文化，弘扬屈原精神”主题阅读倡议，随机抽取了八年级若干名学生，对其周末课外阅读时间进行了调查.根据收集到的数据，整理后得到如下不完整的统计图表(每组包含最小值，不包含最大值)：时长(分)
30~60
60~90
90~120
120~150
组中值
①
75
105
135
频数
6
20
②
4
数据分组后，一个组的两个端点的数的平均数，叫做这个组的组中值.
请你根据图表中提供的信息，解答下面的问题：
(1)、扇形统计图中，120~150分钟时间段对应扇形的圆心角的度数是°，a的值为.样本数据的中位数位于时间段.(2)、请将表格补充完整.(3)、请通过计算估计该校八年级学生周末平均课外阅读时间.21. 实施“双减”政策后，学生学业负担有所减轻，很多家长选择利用周末时间带孩子去景区游玩.某调查小组从去过甲景区和乙景区的学生中各随机抽取了20名学生对这两个景区分别进行评分(单位：分)，并通过整理和分析，给出了部分信息.甲景区得分情况：7，8，7，10，7，6，9，9，10，10，8，9，8，6，6，10，9，7，9，9；
乙景区得分情况：7，8，7，6，7，6，9，9，10，10，8，8，8，6，6，10，8，7，8，8.
抽取的学生对两个景区分别打分的平均数、众数和中位数如下表.
平均数
众数
中位数
甲景区
8.2
9
b
乙景区
7.8
a
8
根据以上信息，解答下列问题：
(1)、a= ， b=.(2)、根据上述数据，你认为去过这两个景区的学生对哪个景区评价更高? 请说明理由(写出一条理由即可).22. 某中学八年级组织了一次数学计算竞赛，每班选25名同学参加竞赛，成绩分为 A，B，C，D 四个等级，其中A等级得分为100分，B等级得分为90分，C等级得分为80分，D等级得分为 70分.数学教研组将八年级一班和二班的成绩整理并绘制成如图的统计图，请根据图中信息解答下列问题.一班竞赛成绩条形统计图 二班竞赛成绩扇形统计图
(1)、把一班竞赛成绩条形统计图补充完整。(2)、求出下表中a，b，c的值.平均数(分)
中位数(分)
众数(分)
一班
a
b
90
二班
87.6
80
C
(3)、请从以下给出的两个方面对这次竞赛成绩的结果进行分析：①从平均数、众数两方面来比较一班和二班的成绩.
②从B级及以上的人数来比较一班和二班的成绩.
23. 甲乙两名同学进行射击训练，在相同条件下各射靶5次，成绩统计如表：命中环数
7
8
9
10
甲命中相应环数的次数
2
2
0
1
乙命中相应环数的次数
1
3
1
0
(1)、计算甲、乙两人的射击成绩的平均数；(2)、若从甲、乙两人射击成绩方差的角度评价两人的射击水平，请通过计算说明：谁的射击成绩更稳定些？24. 为提高学生的数学思维能力，某中学开展“迎元旦数学知识竞赛”，八(1)班、八(2)班各选出5名选手参加竞赛，整理5名选手的竞赛成绩(满分为100分)绘制如图所示的统计图和不完整的统计表．平均数
中位数
众数
八(1)班(分)
87
80
八(2)班(分)
85
(1)、请你把表格补充完整；(2)、结合两班竞赛成绩的平均数中位数和众数，你认为哪个班的竞赛成绩较好；(3)、计算两个班竞赛成绩的方差，并说明哪个班的成绩较为整齐．