2024年浙教版数学八年级下学期第二章一元二次方程单元测试（培优卷）

试卷更新日期：2024-03-05 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知关于x的方程 $(m + 1) x^{2} - 3 = 0$ 是一元二次方程，则m的取值范围是（）

A、m>-1 B、m≠0 C、m=1 D、m≠-1

查看试题解析
2. 将方程 $x^{2} - 2 x = x + 3$ 化成一般形式后，二次项系数和常数项分别是（）

A、-3，3 B、-1，-3 C、1，3 D、1，-3

查看试题解析
3. 用因式分解法解下列方程，变形正确的是（）

A、(3x-3)(3x-4)=0，于是3x-3=0或3x-4=0 B、(x+3)(x-1)=1，于是x+3=1或x-1=1 C、(x-2)(x-3)=6，于是x-2=2或x-3=3 D、x(x+2)=0，于是x+2=0

查看试题解析
4. 已知三角形的两边长分别是8和6，第三边的长是一元二次方程(x-6)(x-10)=0的一个实数根，则该三角形的面积是（）

A、24或2 $\sqrt{5}$ B、24 C、2 $\sqrt{5}$ D、8 $\sqrt{5}$ 或24

查看试题解析
5. 空地上有一段长为20米的旧墙MN，利用旧墙和木栏围成一个矩形菜园DCBA(如图)，已知木栏总长为40米，所围成的菜园面积为 198平方米，则AB的长为（）

A、9米 B、11米 C、(10+ $\sqrt{2}$ )米 D、9米或11米

查看试题解析
6. 一个长方形纸片内放入两个边长分别为3cm和4cm的小正方形纸片，按照图1放置，长方形纸片没有被两个小正方形纸片覆盖的部分(阴影部分)的面积为8cm²；按照图2 放置，长方形纸片没有被两个小正方形纸片覆盖的部分的面积为11 cm².当把两个小正方形纸片按照图3放置时，长方形纸片没有被两个小正方形纸片覆盖的部分的面积为（）

A、5cm² B、6cm² C、7cm² D、8cm²

查看试题解析
7. 已知 $m ， n$ 是一元二次方程 $x^{2} + 2 x - 5 = 0$ 的两个实数根，则 $m^{2} + m n + 2 m$ 等于（）

A、0
B、4
C、8
D、10

查看试题解析
8. 已知m，n是方程x²+2x﹣5=0的两个实数根，则m²﹣mn+3m+n=（　　）

A、6 B、7 C、8 D、9

查看试题解析
9. 关于x的一元二次方程 $k x^{2} - 2 x + 1 = 0$ 有两个实数根，那么实数k的取值范围是（）

A、 $k \leq 1$ B、 $k < 1$ 且 $k \neq 0$ C、 $k \leq 1$ 且 $k \neq 0$ D、 $k \geq 1$

查看试题解析
10. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a - b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；
②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$
其中正确的：（）

A、只有① B、只有①② C、①②③ D、只有①②④

查看试题解析

二、填空题（每题4分，共24分）

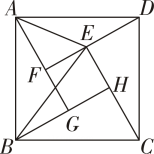
11. 关于x的方程（1-m²）x²+2mx-1=0的所有根都是比1小的正实数，则实数m的取值范围是．

查看试题解析
12. 如图，是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形组成的一个大正方形．设图中AF=a，DF=b，连接AE ，BE，若△ADE与△BEH的面积相等，则 $\frac{b^{2}}{a^{2}} + \frac{a^{2}}{b^{2}}$ =

查看试题解析
13. 某超市销售一种饮料，平均每天可售出100箱，每箱的利润为 12元.为了扩大销售，超市准备适当降价.据测算，若每箱每降价1元，平均每天可多售出 20 箱，如果要使每天销售饮料获利1 400元，那么每箱应降价多少元? 设每箱应降价x 元，则可列方程为
.

查看试题解析
14. 如果关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，若（x﹣1）（mx﹣n）＝0是倍根方程，则 $\frac{2 n}{m}$ 的值为.

查看试题解析
15. 已知关于一元二次方程ax²＋bx＋c＝0(a≠0)，有下列说法：
①若a－b＋c＝0则b²－4ac≥0；②若方程ax²＋bx＋c＝0两根为1和2，则2a－c＝0；③若方程ax²＋c＝0有两个不相等的实根，则方程ax²＋bx＋c＝0必有实根；④若b＝2a＋c，则方程有两个不相等的实数根．

其中正确的是． (填写序号)

查看试题解析
16. 设x₁ ， x₂是一元二次方程x²+5x﹣3=0的两根，且2x₁（x₂²+6x₂﹣3）+a=4，则a= ．

查看试题解析

三、解答题（共8题，共66分）

17. 已知m是方程x²-2x-1=0的一个根，求代数式2m²-4m+19的值

查看试题解析
18. 已知x=1是关于x的一元二次方程x²+ax-b=0的一个解，求代数式a²+b²-2ab的值

查看试题解析
19. 已知关于x的一元二次方程 $x^{2} - 2 m x - 5 m^{2} - 3$ =0.

(1)、当m=1时，试求出该方程的解.

(2)、求证：不论m取何值，该方程总有两个不相等的实数根.

查看试题解析
20. 已知关于x的方程 $x^{2} + 2 x + n = 0 (n \neq 0) .$

(1)、当方程有两个不相等的实数根时，求 n的取值范围.

(2)、当x=n是原方程的一个根时，求n的值与方程的根.

查看试题解析
21. 某种植物主干长出若干数目的分支，每个分支长出相同数目的小分支.若主干、分支、小分支的总数为73，求每个分支长出的小分支的数目

查看试题解析
22. 已知关于x的一元二次方程x²-(2k+1)x+k²+k=0，若△ABC的两边AB，AC的长是这个方程的两个实数根，第三边BC的长为5．

(1)、若k=3，请判断△ABC的形状并说明理由；

(2)、若△ABC是等腰三角形，求k的值．

查看试题解析
23. 已知关于 $x$ 的一元二次方程 $x^{2} + (2 k + 1) x$ $+ k^{2} + 1 = 0$ 有两个不相等的实数根 $x_{1} ， x_{2}$ .

(1)、求实数 $k$ 的取值范围.

(2)、若 $x_{1} ， x_{2}$ 满足 $x_{1} + x_{2} = - x_{1} x_{2}$ ，求 $k$ 的值.

查看试题解析
24. 已知关于x的方程(k-1)x²-2kx+k+2=0有实数根．

(1)、求k的取值范围．

(2)、若x₁ ， x₂是方程(k-1)x²-2kx+k+2=0的两个实数根，问：是否存在实数k，使其满足(k-1)x₁²+2kx₂+k+2=4x₁x₂？若存在，求出k的值；若不存在，请说明理由．

查看试题解析

2024年浙教版数学八年级下学期第二章 一元二次方程 单元测试（培优卷）

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2024年浙教版数学八年级下学期第二章一元二次方程单元测试（培优卷）