吉林省长春市汽开区2023-2024学年七年级上学期期末数学试卷

试卷更新日期：2024-03-05 类型：期末考试

进入出卷网下载

一、选择题（本大题共8小题，每小题3分，共24分）

1. 中国人最早使用负数，可追溯到两千多年前的秦汉时期，则﹣2023的相反数为（）

A、﹣2023 B、2023 C、 $\frac{1}{2023}$ D、- $\frac{1}{2023}$

查看试题解析
2. 杭州奥体博览城是2022年亚运会的主场馆，它的核心区占地154.37公顷，建筑总面积大约有2700000平方米．数据2700000用科学记数法表示为（）

A、27×10⁵ B、2.7×10⁵ C、27×10⁶ D、2.7×10⁶

查看试题解析
3. 如图所示的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 已知a、b两数在数轴上对应的点如图所示，则下列结论正确的是（）

A、a+b＞0 B、a﹣b＞0 C、|a|＞|b| D、ab＜0

查看试题解析
5. 下列各组式子中，是同类项的是（）

A、﹣6xy和xz B、4x²y和0.5xy² C、 $\frac{1}{3}$ x²y和﹣yx² D、2xy和3xyz

查看试题解析
6. 下列说法中，错误的是（）

A、数字0也是单项式 B、单项式﹣x³y的系数为﹣1，次数是3 C、多项式﹣2x³﹣2的常数项是﹣2 D、3x²y²+2y³﹣xy是四次三项式

查看试题解析
7. 如图是一个正方体的展开图，则与”学”字相对的是（）

A、核 B、心 C、数 D、养

查看试题解析
8. 如图，将木条a，b与c钉在一起，∠1＝85°，∠2＝50°，要使木条a与b平行，木条a旋转的度数至少是（）

A、50° B、35° C、25° D、15°

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

9. 比较大小： $- \frac{3}{4}$ $- \frac{4}{5}$ （填“＞”或“＜”）

查看试题解析
10. 用四舍五入法取近似数：3.2652≈（精确到十分位）．

查看试题解析
11. 将多项式3x²﹣1﹣6x⁵﹣4x³按字母x的降幂排列为．

查看试题解析
12. 下列三个日常现象：
其中，可以用“两点之间线段最短”来解释的是（填序号）．

查看试题解析
13. 如图，射线 $O A$ 的方向是北偏东 $26 ° 38'$ ，那么 $∠ α =$ ．

查看试题解析
14. 如图，直线AB∥CD，∠C＝44°，∠E为直角，则∠1＝.

查看试题解析

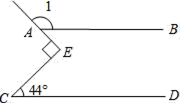
三、解答题（本大题共10个小题，共78分）

15. 计算：

(1)、18+16÷（﹣2）³﹣（﹣4）；

(2)、 $(\frac{1}{2} - \frac{1}{9} + \frac{1}{12}) \times 36$ ．

查看试题解析
16. 化简：

(1)、5a²﹣7﹣3a﹣5+a﹣2a²；

(2)、（2a²b﹣ab²）﹣2（ab²+3a²b）．

查看试题解析
17. 已知C为线段AB的中点，D在线段CB上，且DA＝6，DB＝4，求CD的长度．

查看试题解析
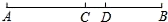18. 如图所示的正方形网格，小正方形的顶点称为格点．点A、B、C均在格点上，只用无刻度的直尺在给定的网格中按要求画图，不要求写作法．

(1)、画射线AC．

(2)、过点B画AC的平行线BD，点D在格点上．

(3)、在射线AC上取一点E，画线段BE，使其长度表示点B到AC的距离．

查看试题解析
19. 先化简，再求值：2xy+（3xy﹣2y²）﹣2（xy﹣y²），其中x＝﹣1，y＝2．

查看试题解析
20. 如图，学校要利用专款建一长方形的自行车停车场，其他三面用护栏围起，其中长方形停车场的长为（2a+3b）米，宽比长少（a﹣b）米．

(1)、用a、b表示长方形停车场的宽；

(2)、求护栏的总长度；

(3)、若a＝30，b＝10，每米护栏造价80元，求建此停车场所需的费用．

查看试题解析
21. 如图：已知直线AB、CD相交于点O，EO⊥CD．

(1)、若∠AOC＝34°，求∠BOE的度数；

(2)、若∠BOD：∠BOC＝1：4，直接写出∠AOE＝．

查看试题解析
22. 吉大力旺中学召开运动会，初一某班需要购买运动鞋和短裤，运动鞋每双定价200元，短裤每条定价50元．某商店开展促销活动，可以向客户提供两种优惠方案：
方案一：买一双运动鞋送一条短裤；
方案二：运动鞋和短裤都按定价的90%付款．
现某班要购买运动鞋20双，短裤x条（x＞20的整数）．

(1)、若该班按方案一购买，求需付款多少元（用含x代数式表示）；

(2)、若该班按方案二购买，求需付款多少元（用含x代数式表示）；

(3)、当x＝30时，哪种方案更划算？请通过计算说明理由．

查看试题解析
23. 如图

(1)、【感知】已知：如图①，点E在AB上，且CE平分∠ACD，∠1＝∠2．求证：AB∥CD．
将下列证明过程补充完整：
证明：∵CE平分∠ACD（已知），
∴∠2＝∠    ▲        （角平分线的定义），
∵∠1＝∠2（已知），
∴∠1＝∠    ▲        （等量代换），
∴AB∥CD（      ）．

(2)、【探究】已知：如图②，点E在AB上，且CE平分∠ACD，AB∥CD．求证：∠1＝∠2．

(3)、【应用】如图③，BE平分∠DBC，点A是BD上一点，过点A作AE∥BC交BE于点E，∠ABC：∠BAE＝4：5，直接写出∠E的度数．

查看试题解析
24. 如图

(1)、【材料阅读】
如图①，数轴上的点A、B表示的数分别为﹣1、7，C是线段AB的中点．
点C表示的数是．

(2)、若点P、Q分别从点C、B同时出发，以每秒3个单位长度和1个单位长度的速度沿数轴正方向运动，则t秒后，点P、Q表示的数分别是、．（用含t的代数式表示）

(3)、在（2）的条件下，若P、Q两点之间的距离为2，求t的值．

(4)、【方法迁移】
如图②，∠AOB＝140°，OC平分∠AOB．现有射线OP、OQ分别从OC、OB同时出发，以每秒15°和每秒10°的速度绕点O顺时针旋转，当OP旋转一周时，这两条射线都停止旋转．问经过几秒后，射线OP、OQ的夹角为30°，直接写出t的值．

查看试题解析