吉林省吉林市丰满区2023-2024学年八年级上学期期末考试数学试题
试卷更新日期：2024-03-05 类型：期末考试
一、单项选择题（每小题2分，共12分）
-
1. x满足什么条件时分式有意义（ ）A、x≠0 B、x≠±5 C、x≠－5 D、x≠52. 下列图形中具有稳定性的是（ ）A、
B、
C、
D、
3. 在下列计算中，正确的是（ ）A、a3•a3=3a6 B、（－3a2）3=－27a6 C、a3＋a4=a7 D、a6÷a2=a34. 若等腰三角形的一个角为70°，则它的底角为（ ）A、55° B、70° C、55°或70° D、40°或70°5. 若16x2＋mx＋1是完全平方式，则m的值是（ ）A、±8 B、±4 C、8 D、－86. 如图，在3×3的网格中，每个网格线的交点称为格点，A，B在两个格点上，请在图中再寻找另一个格点C，使△ABC成为等腰三角形，则满足条件的C点的个数为（ ）
A、10个 B、8个 C、6个 D、4个二、填空题（每小题3分，共24分）
-
7. 在平面直角坐标系中，点A（2，6）关于y轴对称的点B的坐标是.8. 分解因式：m3n－mn=.9. 若等腰三角形有两条边长分别为1和3，则其周长为.10. 若一个正多边形的一个外角为30°，则这个正多边形的边数是.11. 如图，△ABC与△A'B'C'关于直线l对称，∠B的度数是.
12. 如图，在△ABC中，分别以点A和点B为圆心，大于的长为半径作弧，两弧相交于M，N两点，作直线MN，交BC于点D，连接AD，若△ADC的周长为5cm，AB=3cm，则△ABC的周长为cm.
13. 如图，在△ABC中，M为边BC的中点，ME⊥AB于点E，MF⊥AC于点F，且BE=CF．若∠BME=25°，则∠A=°.
14. 如图，△ABC是等边三角形，AD是BC边上的高．E是AC边中点，点M是AD上的一个动点，当MC＋ME最小时，∠CME=°.
三、解答题（每小题5分，共20分）
-
15. 运用完全平方公式计算：（4m－3n）2.16. 计算：17. 解方程： ．18. 先化简，再求值： ， 其中x=－1.
四、解答题（每小题7分，共28分）
-
19. 如图，AC=EB，∠ACB=∠EBD，BC=DB，求证△ABC≌△EDB.
20. 如图，在△ABC中，∠C=90°，AD平分∠BAC，AB=17，DC=5，求S△ABD.
21. 在3×3的方格纸中，每个小正方形的顶点为格点，以格点为顶点的三角形称为格点三角形．图中△ABC是一个格点三角形.请在图①和图②中各画出一个与△ABC成轴对称的格点三角形，并画出对称轴.
22. 如图，在△ABC中，AC=2n，∠B=∠ACB=15°，∠D=90°，求CD的长（用含n的式子表示）.
五、解答题（每小题8分，共16分）
-
23. 两个工程队共同参与一项筑路工程，甲队单独施工1个月完成总工程的 ， 这时增加了乙队，两队又共同工作了半个月，总工程全部完成.(1)、设乙队单独施工1个月能完成总工程的 ， 两队半个月完成总工程的（用含x的式子表示）.(2)、哪个队的施工速度快？24. 如图，在△ABC中，AB=AC，D是BC边的中点，连接 AD，BM平分∠ABC，交AC于点M，过点M作MN∥BC，交AB于点N.
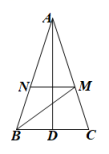(1)、若∠C=72°，求∠BAD的度数.(2)、求证：NB= NM.六、解答题（每小题10分，共20分）
-
25. 如图，在三角形ABC中，AB=BC=AC=8，点M从点A出发，沿折线A-B-C-A以每秒4个单位长度的速度向终点A运动.点N从点B出发，沿折线B-C-A以每秒2个单位长度的速度运动．M，N两点同时出发，点M停止时，点N也随之停止.设点M运动的时间为t秒．
(1)、当M，N两点重合时，求t的值．(2)、当△BMN是以MN为底边的等腰三角形时，求t的值．(3)、直接写出∠BMN=90°时t的值．26. 用图①中的1张边长为m的正方形M图纸、1张边长为n的正方形N图纸和2张边长分别为m，n的长方形D图纸拼成图②的一张大正方形图片，观察图形，并解答下列问题.
(1)、由图②和图①可以得到关于面积的等式为.(2)、小丽同学用图①中这三张图纸拼出一张面积为（2m+3n）（3m+2n）的大长方形图片，求需要M，N，D三种纸片各多少张.(3)、如图③，已知点P为线段AF上的动点，分别以PF，AP为边在AF的两侧作正方形PMEF和正方形APCD.若AF=5，且两个正方形的面积之和为S1＋S2=13，利用（1）中得到的结论求图③中阴影部分面积S△PCF.