吉林省白山市江源区2023-2024学年八年级上学期12月期末数学试题

试卷更新日期：2024-03-05 类型：期末考试

进入出卷网下载

一、选择题（每小题2分，共12分）

1. 下列长度的三条线段，能组成三角形的是（　　）

A、2cm，3cm，6cm B、5cm，20cm，20cm C、7cm，1cm，3cm D、5cm，4cm，9cm

查看试题解析
2. 下面四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（　　）

A、a⁴•a³＝a¹² B、a⁸÷a⁴＝a² C、a³+a³＝2a⁶ D、（a²）⁴＝a⁸

查看试题解析
4. 如图，将两根钢条AA'、BB'的中点O连在一起，使AA'、BB'可以绕着点O自由旋转，就做成了一个测量工件，则A'B'的长等于内槽宽AB，那么判定△OAB≌△OA'B'的理由是（）

A、SSS B、SAS C、AAS D、ASA

查看试题解析
5. 在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是（）

A、点M B、点N C、点P D、点Q

查看试题解析
6. 有一块直角三角板DEF放置在△ABC上，三角板DEF的两条直角边DE、DF恰好分别经过点B、C ，在△ABC中， $∠ D B A + ∠ D C A = 45 °$ ，则∠A的度数是（）

A、 $40 °$ B、 $44 °$ C、 $45 °$ D、 $50 °$

查看试题解析

二、填空题（每小题3分，共24分）

7. 若 $\frac{1}{\sqrt{x - 3}}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
8. 因式分解：4a²﹣1＝.

查看试题解析
9. （3a²﹣6ab）÷3a= ．

查看试题解析
10. 若一个多边形内角和为900°，则这个多边形是边形．

查看试题解析
11. 已知点P（﹣2，3）关于x轴的对称点P₁的坐标是．

查看试题解析
12. 如图，AB∥CD，AD与BC交于点E，EF是∠BED的平分线，若∠1=30°，∠2=40°，则∠BEF=度．

查看试题解析
13. 如图，在△ABC中，∠B＝30°，BC的垂直平分线交AB于点E，垂足为点D，若ED＝5，则EC的长为．

查看试题解析
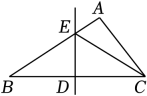14. 如图（1）是长方形纸带，∠DEF＝m，将纸带沿EF折叠成图（2），再沿BF折叠成图（3），则图（3）中的∠CFE度数（用含m的代数式表示）．

查看试题解析

三、解答题（每小题5分，共20分）

15. 计算：（﹣5）³÷（ $\frac{1}{2}$ ）^﹣¹+（3.14﹣π）⁰﹣|﹣ $\sqrt{2}$ +1|．

查看试题解析
16. 先化简，再求值 $(\frac{1}{m - 3} + \frac{1}{m + 3}) \div \frac{2 m}{m^{2} - 6 m + 9}$ ，其中m= $\frac{1}{2}$ 。

查看试题解析
17. 解方程： $\frac{2}{3 x - 3} + \frac{1}{1 - x} = 1$ ．

查看试题解析
18. 如图所示， $A C ⊥ B C$ ， $D C ⊥ E C$ ，垂足均为点C，且 $A C = B C$ ， $E C = D C$ ．求证： $A E = B D$ ．

查看试题解析

四、解答题（每小题7分，共28分）

19. 如图，△ABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，5）．

(1)、若△A'B'C'与△ABC关于x轴成轴对称，作出△A'B'C'；

(2)、若P为y轴上一点，使得△APC周长最小，在图中作出点P，并写出P点的坐标为 ▲ ；

(3)、计算△ABC的面积．

查看试题解析
20. 如图，在△ABC中，AD是高，角平分线AE，BF相交于点O，∠BAC＝50°，∠C＝70°，求∠DAC和∠BOA的大小．

查看试题解析
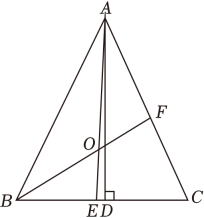21. 下面是小明设计的“作一个含30°角的直角三角形”的尺规作图过程．
已知：如图1，直线l及直线l上一点A．
求作：△ABC，使得∠ACB＝90°，∠ABC＝30°．
作法：如图2，
①在直线l上取点D；
②分别以点A，D为圆心，AD长为半径画弧，交于点B，E；
③作直线BE，交直线l于点C；
④连接AB．
△ABC就是所求作的三角形．
根据小明设计的尺规作图过程，

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明：
证明：连接BD，EA，ED．
∵BA＝BD＝AD，
∴△ABD是等边三角形．
∴∠BAD＝60°．
∵BA＝BD，EA＝    ▲         ，
∴点B，E在线段AD的垂直平分线上（     ）（填推理的依据）．
∴BE⊥AD．
∴∠ACB＝90°．
∴∠ABC+∠BAD＝90°（　               　）（填推理的依据）．
∴∠ABC＝30°．

查看试题解析
22. 如图，已知某船于上午8点在A处观测小岛C在北偏东60°方向上．该船以每小时40海里的速度向东航行到B处，此时测得小岛C在北偏东30°方向上．船以原速度再继续向东航行2小时到达小岛C的正南方D点．求船从A到D一共走了多少海里？

查看试题解析

五、解答题（每小题8分，共16分）

23. 李明到离家2.1千米的学校参加初三联欢会，到学校时发现演出道具还放在家中，此时距联欢会开始还有42分钟，于是他立即匀速步行回家，在家拿道具用了1分钟，然后立即匀速骑自行车返回学校．已知李明骑自行车到学校比他从学校步行到家用时少20分钟，且骑自行车的速度是步行速度的3倍．

(1)、李明步行的速度（单位：米/分）是多少？

(2)、李明能否在联欢会开始前赶到学校？

查看试题解析
24. 如图1，将一个长为4a，宽为2b的长方形，沿图中虚线均匀分成4个小长方形，然后按图2形状拼成一个正方形.

(1)、图2的空白部分的边长是多少？（用含a、b的式子表示）

(2)、若2a+b＝7，且ab＝3，求图2中的空白正方形的面积.

(3)、观察图2，用等式表示出（2a﹣b）² ， ab和（2a+b）²的数量关系.

查看试题解析

六、解答题（每小题10分，共20分）

25. 某茶店用4000元购进了A种茶叶若干盒，用8400元购进了B种茶叶若干盒，所购B种茶叶比A种茶叶多10盒，且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍．
（Ⅰ）A，B两种茶叶每盒进价分别为多少元？
（Ⅱ）若第一次所购茶叶全部售完后，第二次购进A，B两种茶叶共100盒（进价不变），A种茶叶的售价是每盒300元，B种茶叶的售价是每盒400元，两种茶叶各售出一半后，为庆祝元旦，两种茶叶均打七折销售，全部售出后，第二次所购茶叶的利润为5800元（不考虑其他因素），求本次购进A，B两种茶叶各多少盒？

查看试题解析
26. 通过对下面数学模型的研究学习，解决下列问题：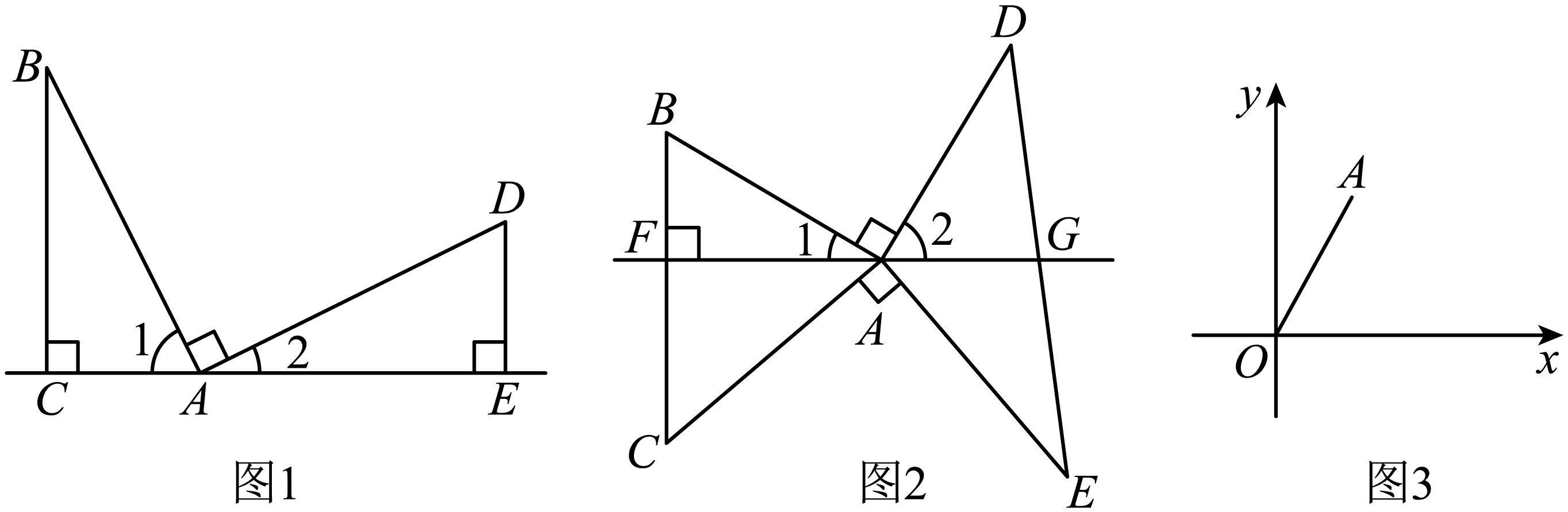

(1)、【模型呈现】
如图1， $∠ B A D ＝ 90 ° ， A B ＝ A D$ ，过点B作 $B C ⊥ A C$ 于点C，过点D作 $D E ⊥ A C$ 于点E．由 $∠ 1 + ∠ 2 = ∠ 2 + ∠ D = 90 °$ ，得 $∠ 1 = ∠ D$ ．又 $∠ A C B = ∠ A E D = 90 °$ ，可以推理得到 $△ A B C ≌ △ D A E$ ．进而得到AC＝， BC＝．我们把这个数学模型称为“K字”模型或“一线三等角”模型；

(2)、【模型应用】
①如图2， $∠ B A D = ∠ C A E = 90 ° ， A B ＝ A D ， A C ＝ A E$ ，连接 $B C ， D E$ ，且 $B C ⊥ A F$ 于点F， $D E$ 与直线 $A F$ 交于点G．求证：点G是 $D E$ 的中点；
②如图3，在平面直角坐标系xOy中，点A的坐标为 $(2 ， 4)$ ，点B为平面内任一点．若 $△ A O B$ 是以 $O A$ 为斜边的等腰直角三角形，请直接写出点B的坐标．

查看试题解析