四川省攀枝花市2023年中考数学真题
试卷更新日期:2024-03-05 类型:中考真卷
一、选择题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
-
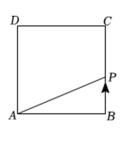
1. 的绝对值是( )A、 B、 C、 D、2. 下列各数是不等式x-1≥0的解的是( )A、-2 B、-1 C、0 D、13. 将数据用科学记数法表示正确的是( )A、 B、 C、 D、4. 计算 , 以下结果正确的是( )A、 B、 C、 D、无意义5. 以下因式分解正确的是( )A、 B、 C、 D、6. 中,、、的对边分别为、、已知 , , , 则的值为( )A、 B、 C、 D、7. 为了回馈客户,商场将定价为元的某种儿童玩具降价进行销售“六一”儿童节当天,又将该种玩具按新定价再次降价销售,那么该种玩具在儿童节当天的销售价格为( )A、元 B、元 C、元 D、元8. 已知的周长为 , 其内切圆的面积为 , 则的面积为( )A、 B、 C、 D、9. 如图,正方形的边长为 , 动点从点出发沿折线做匀速运动,设点运动的路程为 , 的面积为 , 下列图象能表示与之间函数关系的是( )
 A、
A、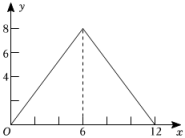 B、
B、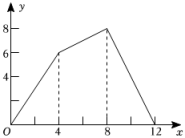 C、
C、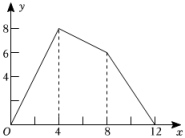 D、
D、 10. 每次监测考试完后,老师要对每道试题难度作分析已知:题目难度系数该题参考人数得分的平均分该题的满分上期全市八年级期末质量监测,有名学生参考数学选择题共设置了道单选题,每题分最后一道单选题的难度系数约为 , 学生答题情况统计如表:
10. 每次监测考试完后,老师要对每道试题难度作分析已知:题目难度系数该题参考人数得分的平均分该题的满分上期全市八年级期末质量监测,有名学生参考数学选择题共设置了道单选题,每题分最后一道单选题的难度系数约为 , 学生答题情况统计如表:选项
留空
多选
人数
占参考人数比
根据数据分析,可以判断本次监测数学最后一道单选题的正确答案应为( )
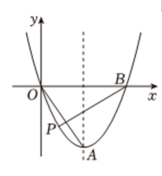
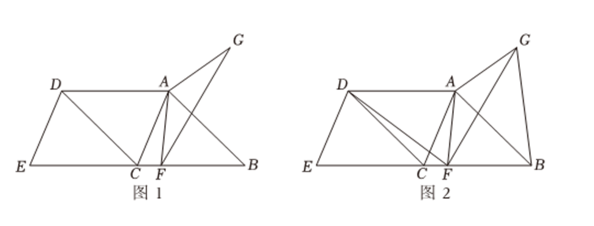
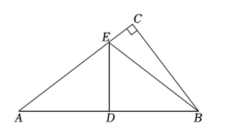
A、 B、 C、 D、11. 如图,已知正方形的边长为 , 点是对角线上的一点,于点 , 于点 , 连接 , 当::时,则( )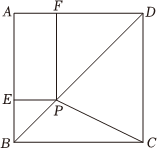 A、 B、 C、 D、12. 我们可以利用图形中的面积关系来解释很多代数恒等式给出以下组图形及相应的代数恒等式:
A、 B、 C、 D、12. 我们可以利用图形中的面积关系来解释很多代数恒等式给出以下组图形及相应的代数恒等式: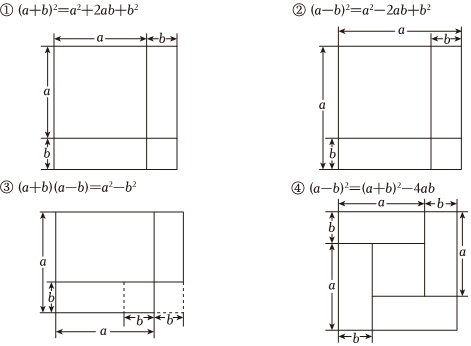
其中,图形的面积关系能正确解释相应的代数恒等式的有( )A、个 B、个 C、个 D、个二、填空题(本大题共4小题,共20.0分)
-
13. 的两根分别为、 , 则 .14. 如图,在中, , , 线段的垂直平分线交于点 , 交于点 , 则 .
 15. 如图,在正方形中,分别以四个顶点为圆心,以边长的一半为半径画圆弧,若随机向正方形内投一粒米米粒大小忽略不计 , 则米粒落在图中阴影部分的概率为 .
15. 如图,在正方形中,分别以四个顶点为圆心,以边长的一半为半径画圆弧,若随机向正方形内投一粒米米粒大小忽略不计 , 则米粒落在图中阴影部分的概率为 .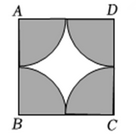 16. 如图,在直角中, , , 将绕点顺时针旋转至的位置,点是的中点,且点在反比例函数的图象上,则的值为 .
16. 如图,在直角中, , , 将绕点顺时针旋转至的位置,点是的中点,且点在反比例函数的图象上,则的值为 .
三、解答题(本大题共8小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 解不等式组: .18. 已知 , 求的值.19. 如图,点和是一次函数的图象与反比例函数的图象的两个交点.
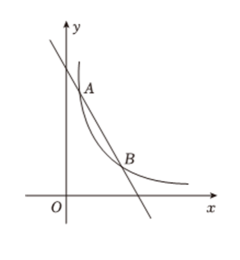 (1)、求一次函数与反比例函数的表达式;(2)、当为何值时,?20. 如图,为的直径,如果圆上的点恰使 , 求证:直线与相切.
(1)、求一次函数与反比例函数的表达式;(2)、当为何值时,?20. 如图,为的直径,如果圆上的点恰使 , 求证:直线与相切.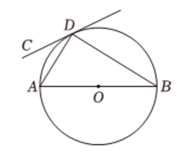 21. 年卡塔尔世界杯共有支球队进行决赛阶段的比赛决赛阶段分为分组积分赛和复赛支球队通过抽签被分成个小组,每个小组支球队,进行分组积分赛,分组积分赛采取单循环比赛同组内每支球队之间都只进行一场比赛 , 各个小组的前两名共支球队将获得出线资格,进入复赛;进入复赛后均进行单场淘汰赛,支球队按照既定的规则确定赛程,不再抽签,然后进行决赛,决赛,最后胜出的支球队进行半决赛,半决赛胜出的支球队决出冠、亚军,另外支球队决出三、四名.(1)、本届世界杯分在组的支球队有阿根廷、沙特、墨西哥、波兰,请用表格列一个组分组积分赛对阵表不要求写对阵时间 .
21. 年卡塔尔世界杯共有支球队进行决赛阶段的比赛决赛阶段分为分组积分赛和复赛支球队通过抽签被分成个小组,每个小组支球队,进行分组积分赛,分组积分赛采取单循环比赛同组内每支球队之间都只进行一场比赛 , 各个小组的前两名共支球队将获得出线资格,进入复赛;进入复赛后均进行单场淘汰赛,支球队按照既定的规则确定赛程,不再抽签,然后进行决赛,决赛,最后胜出的支球队进行半决赛,半决赛胜出的支球队决出冠、亚军,另外支球队决出三、四名.(1)、本届世界杯分在组的支球队有阿根廷、沙特、墨西哥、波兰,请用表格列一个组分组积分赛对阵表不要求写对阵时间 .
(2)、请简要说明本届世界杯冠军阿根廷队在决赛阶段一共踢了多少场比赛?
(3)、请简要说明本届世界杯支球队在决赛阶段一共踢了多少场比赛?22. 拜寺口双塔,分为东西两塔,位于宁夏回族自治区银川市贺兰县拜寺口内,是保存最为完整的西夏佛塔,已有近年历史,是中国佛塔建筑史上不可多得的艺术珍品某数学兴趣小组决定采用我国古代数学家赵爽利用影子对物体进行测量的原理,来测量东塔的高度东塔的高度为 , 选取与塔底在同一水平地面上的、两点,分别垂直地面竖立两根高为的标杆和 , 两标杆间隔为 , 并且东塔、标杆和在同一竖直平面内从标杆后退到处即 , 从处观察点,、、在一直线上;从标杆后退到处即 , 从处观察点,、、三点也在一直线上,且、、、、在同一直线上,请你根据以上测量数据,帮助兴趣小组求出东塔的高度.