初中数学同步训练必刷培优卷（北师大版七年级下册第一单元测试卷）

试卷更新日期：2024-03-05 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列运算中，正确的是（）

A、 $3 a^{2} - a^{2} = 2$ B、 ${(2 a^{2})}^{2} = 2 a^{4}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 $a^{3} \cdot a^{2} = a^{5}$

查看试题解析
2. 若( $(x^{2} + a x) (x^{2} - 3 x - 9 b)$ 的乘积中不含x²和x³的项，则ab的值为（）

A、 $\frac{1}{3}$ B、3 C、 $- \frac{1}{3}$ D、-3

查看试题解析
3. 设( $(a + 2 b)^{2} = (a - 2 b)^{2} + A_{1}$ ，则单项式A等于（）

A、8ab B、-8ab C、8b² D、4ab

查看试题解析
4. 如图在边长为a的正方形纸片中剪去一个边长为b的小正方形，把余下的部分沿虚线剪开，拼成一个矩形，分别计算这两个图形阴影部分的面积，可以验证的等式是（）

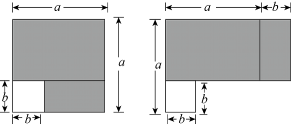A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $a^{2} + a b = a (a + b)$

查看试题解析
5. 下列多项式相乘，能用平方差公式计算的是（）

A、 $(x + 2) (x + 2)$ B、 $(- x + y) (x - y)$ C、 $(2 x - y) (2 x + y)$ D、 $(- x - y) (x + y)$

查看试题解析
6. 如图1，有边长分别为a和b（a>b）的A类和B类正方形纸片、长为a、宽为b的C类矩形纸片若干张，要拼一个边长为a+b的正方形（如图2所示），则需要1张A类纸片、1张B类纸片和⒉张C类纸片.若要拼一个长为3a+b、宽为2a+2b的矩形，则需要C类纸片的张数为（）

A、6 B、7 C、8 D、9

查看试题解析
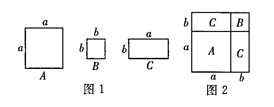7. 已知 $x - \frac{1}{x} = 2$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值为（）

A、2 B、4 C、6 D、8

查看试题解析
8. 国际数学家大会是数学界的最高水平盛典，大合邀请著名数学粽子者，交流报告数学最新迸展和成果，由承办国的国泉元曾颁发世界数学最高奖——菲尔兹奖.2002年在北京召开了国数学家大会，会标图案是我国古代著名的”赵爽弦图”．图中包合四个面积为24的全等的直角三角形，围成的大正方形面积为100．则直角三角形中较长直角边与较短直角边的长度差为（）

A、2 B、4 C、6 D、8

查看试题解析
9. 如图，美美不小心在课后作业的第1题滴了一点墨水，留下一道残缺不全的题目，则被墨水覆盖的部分为（）

A、 $x^{3} - x^{2} + x$ B、 $- x^{3} - x^{2} + x$ C、 $- x^{3} + x^{2} - x$ D、 $x^{3} + x^{2} - x$

查看试题解析
10. 有 $n$ 个依次排列的整式：第 $1$ 项是 $(x + 1)$ ，用第 $1$ 项乘 $(x - 1)$ ，所得之积记为 $a_{1}$ ，将第 $1$ 项加上 $(a_{1} + 1)$ 得到第 $2$ 项，再将第 $2$ 项乘 $(x - 1)$ 得到 $a_{2}$ ，将第 $2$ 项加上 $(a_{2} + 1)$ 得到第 $3$ 项 $\dots \dots$ 以此类推，某数学兴趣小组对此展开研究，得到下列 $4$ 个结论：
$①$ 第 $4$ 项为 $x^{4} + x^{3} + x^{2} + x + 1$ ；
$② a_{5} = x^{5} - 1$ ；
$③$ 若第 $2023$ 项的值为 $0$ ，则 $x^{2024} = 1$ ．
以上结论正确的个数为（）

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个

查看试题解析

二、填空题（每题3分，共15分）

11. 已知a＝2023x+2023，b＝2023x+2024，c＝2023x+2025，则a²+b²+c²-ab-ac-bc的值是．

查看试题解析
12. 已知 $(x^{2} + m x + n) (x^{2} - 3 x + 2)$ 的展开式中不含 $x^{2}$ 和 $x^{3}$ 项，则 $m + n =$ ．

查看试题解析
13. 有一个正方形的花园，如果它的边长增加 $2 m$ ，那么花园面积将增加 $16 m^{2}$ ，则原花园的面积为．

查看试题解析
14. 观察下列各数，按照某种规律在横线上填上一个适当的数。
$- \frac{1}{4}$ ， $\frac{2}{8}$ ， $- \frac{3}{16}$ ， $\frac{4}{32}$ ， $- \frac{5}{64}$ ，.

查看试题解析
15. 如图，长方形 $A B C D$ 中放入一个边长为 $8$ 的大正方形 $A L M N$ 和两个边长为6的小正方形 $D E F G$ 及正方形 $H I J K$ ．

(1)、若阴影部分 $S_{2}$ 与 $S_{3}$ 为正方形，且 $S_{2}$ 的面积为1，则 $S_{3} =$ ．

(2)、若3个阴影部分的面积满足 $2 S_{3} + S_{1} - S_{2} = 12$ ，则长方形 $A B C D$ 的面积为．

查看试题解析

三、综合题

16.

(1)、已知m+4n﹣3＝0，求2^m•16ⁿ的值；

(2)、已知n为正整数，且x²ⁿ＝4，求（x³ⁿ）²﹣2（x²）²ⁿ的值．

查看试题解析
17. 如图

(1)、数学课堂上老师留了一道数学题，如图①，用式子表示空白部分的面积，
甲、乙两名同学表示的式子是：甲：10×6-10x-6x；乙：（10- x）（6-x）．
正确的学生是

(2)、如图②，有一块长为（8a+3b）米。宽为（7a-3b）米的长方形空地，计划修筑东西、南北走向的两条道路。其余进行绿化。已知两条道路的宽分别为2a米和3a米，求绿化的面积．（用含a，b的式子来表示）

查看试题解析
18.
阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如 $3 + 2 \sqrt{2} = (1 + \sqrt{2})^{2}$ 善于思考的小明进行了以下探索：设 $a + b \sqrt{2} = (m + n \sqrt{2})^{2}$ ， $($ 其中 $a$ 、 $b$ 、 $m$ 、 $n$ 均为整数 $)$ ，则有 $a + b \sqrt{2} = m^{2} + 2 n^{2} + 2 m n \sqrt{2}$ ， $∴ a = m^{2} + 2 n^{2}$ ， $b = 2 m n .$ 这样小明就找到了一种把类似 $a + b \sqrt{2}$ 的式子化为平方式的方法 $.$ 请你仿照小明的方法探索并解决下列问题：

(1)、当 $a$ 、 $b$ 、 $m$ 、 $n$ 均为整数时，若 $a + b \sqrt{5} = (m + n \sqrt{5})^{2}$ ，用含 $m$ 、 $n$ 的式子分别表示 $a$ 、 $b$ ，得： $a =$ ， $b =$ ．

(2)、利用所探索的结论，找一组正整数 $a$ 、 $b$ 、 $m$ 、 $n$ ，填空： $+$ $\sqrt{5} = ($ $+$ $\sqrt{5})^{2}$ ．

(3)、若 $a + 6 \sqrt{5} = (m + n \sqrt{5})^{2}$ ，且 $a$ 、 $m$ 、 $n$ 均为正整数，求 $a$ 的值．

查看试题解析
19. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1可以得到 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，请解答下列问题：

(1)、写出图2中所表示的数学等式.

(2)、根据整式乘法的运算法则，通过计算验证上述等式.

(3)、利用（1）中得到的结论，解决下面的问题：若 $a + b + c = 18$ ， $a^{2} + b^{2} + c^{2} = 116$ ，则 $a b + a c + b c =$ .

查看试题解析
20. 18世纪欧拉引进了求和符号“ $\sum_{k = i}^{n} k$ ”（其中 $i \leq n$ ，且i和n表示正整数），对这个符号我们进行如下定义： $\sum_{k = i}^{n} k$ 表示k从i开始取数一直取到n，全部加起来，即 $\sum_{k = i}^{n} k = i + (i + 1) + (i + 2) + (i + 3) + \cdot \cdot \cdot + n$ ．例如：当i=1时， $\sum_{k = 1}^{n} k = 1 + 2 + 3 + 4 + \cdot \cdot \cdot + n$ ．

(1)、① $\sum_{k = 1}^{9} k$ ， ② $\sum_{k = 9}^{12} k$ ， ③ $\sum_{k = 14}^{16} k$ 中和为45的是；（填写编号）

(2)、 $\sum_{k = 3}^{5} (1 + k) =$ ；

(3)、 $\sum_{k = 3}^{n} (2 - k) =$ ；（用含n的式子表示）

(4)、若 $\sum_{k = 2}^{n} (x - k) (x - k + 1) = 3 x^{2} + p x + m$ ，则 $n =$ ， $p =$ ， $m =$ ．

查看试题解析

21. 阅读下面的材料：

材料一：比较 $3^{22}$ 和 $4^{11}$ 的大小．	材料二：比较 $2^{8}$ 和 $8^{2}$ 的大小．
解：因为 $4^{11} = {(2^{2})}^{11} = 2^{22}$ ，且 $3 > 2$ ，所以 $3^{22} > 2^{22}$ ，即 $3^{22} > 4^{11}$ ．	解：因为 $8^{2} = {(2^{3})}^{2} = 2^{6}$ ，且 $8 > 6$ ，所以 $2^{8} > 2^{6}$ ，即 $2^{8} > 8^{2}$ ．
小结：指数相同的情况下，通过比较底数的大小，来确定两个幂的大小．	小结：底数相同的情况下，通过比较指数的大小，来确定两个幂的大小．

解决下列问题：

(1)、比较

3^{44}

，

4^{33}

，

5^{22}

的大小；

(2)、比较

8 1^{31}

，

2 7^{41}

，

9^{61}

的大小．

查看试题解析

22. 如图1，边长为 $a$ 的正方形中有一个边长为 $b$ 的小正方形，图2是由图1中阴影部分拼成的一个长方形，设图1中阴影部分面积为 $S_{1}$ ，图2中阴影部分面积为 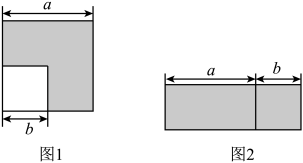$S_{2}$ ．

(1)、请直接用含 $a$ 和 $b$ 的代数式表示 $S_{1} =$ ， $S_{2} =$ ；写出利用图形的面积关系所得到的公式：（用式子表示）．

(2)、依据这个公式，康康展示了“计算： $(2 + 1) \times (2^{2} + 1) \times (2^{4} + 1) \times (2^{8} + 1)$ ”的解题过程．
解：原式 $= (2 - 1) \times (2 + 1) \times (2^{2} + 1) \times (2^{4} + 1) \times (2^{8} + 1)$
$= (2^{2} - 1) \times (2^{2} + 1) \times (2^{4} + 1) \times (2^{8} + 1)$
$= (2^{4} - 1) \times (2^{4} + 1) \times (2^{8} + 1)$
$= (2^{8} - 1) \times (2^{8} + 1)$
$= 2^{16} - 1$ ．
请仿照康康的解题过程计算： $2 \times (3 + 1) \times (3^{2} + 1) \times (3^{4} + 1) \times (3^{8} + 1) + 1$ ．

(3)、对数学知识要会举一反三，请用（1）中的公式证明：任意两个相邻奇数的平方差必是 $8$ 的倍数．

查看试题解析

初中数学同步训练必刷培优卷（北师大版七年级下册 第一单元测试卷）

一、选择题（每题3分，共30分）

二、填空题（每题3分，共15分）

三、综合题

初中数学同步训练必刷培优卷（北师大版七年级下册第一单元测试卷）