【北师大版·数学】2024年中考二轮复习之投影与视图
试卷更新日期:2024-03-05 类型:二轮复习
一、选择题
-
1. 如图所示几何体的主视图是( )
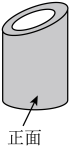 A、
A、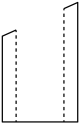 B、
B、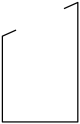 C、
C、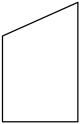 D、
D、 2. 如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图,则所需的小正方体的个数最多是( )
2. 如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图,则所需的小正方体的个数最多是( )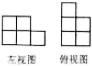 A、7 B、8 C、9 D、103. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( )
A、7 B、8 C、9 D、103. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( ) A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似4. 如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m.则路灯的高度OP为( )
A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似4. 如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4.5m.则路灯的高度OP为( ) A、3m B、4m C、4.5m D、5m5. 观察如图所示的几何体,下列关于其三视图的说法正确的是( )
A、3m B、4m C、4.5m D、5m5. 观察如图所示的几何体,下列关于其三视图的说法正确的是( ) A、主视图既是中心对称图形,又是轴对称图形 B、左视图既是中心对称图形,又是轴对称图形 C、俯视图既是中心对称图形,又是轴对称图形 D、主视图、左视图、俯视图都是中心对称图形6. 佳佳练习几何体素描(如图),其中几何体的主视图是轴对称图形但不是中心对称图形的为( )
A、主视图既是中心对称图形,又是轴对称图形 B、左视图既是中心对称图形,又是轴对称图形 C、俯视图既是中心对称图形,又是轴对称图形 D、主视图、左视图、俯视图都是中心对称图形6. 佳佳练习几何体素描(如图),其中几何体的主视图是轴对称图形但不是中心对称图形的为( ) A、圆锥 B、正方体 C、圆柱 D、球7. 下列对如图物体三视图描述正确的是( )
A、圆锥 B、正方体 C、圆柱 D、球7. 下列对如图物体三视图描述正确的是( )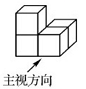 A、左视图和俯视图相同 B、主视图和左视图相同 C、主视图和俯视图相同 D、三视图都相同8.
A、左视图和俯视图相同 B、主视图和左视图相同 C、主视图和俯视图相同 D、三视图都相同8.由4个正方体搭成的几何体按如图放置,若要求画出它的三视图,则在所画的俯视图中正方形共有( )
 A、1个 B、2个 C、3个 D、4个9. 教学楼里的大型多功能厅建成阶梯形状是为了( ).A、美观 B、宽敞明亮 C、减小盲区 D、容纳量大10. 如图,由6个同样大小的正方体摆成的几何体,在正方体①的正上方再放一个这样的正方体,所得的几何体( )
A、1个 B、2个 C、3个 D、4个9. 教学楼里的大型多功能厅建成阶梯形状是为了( ).A、美观 B、宽敞明亮 C、减小盲区 D、容纳量大10. 如图,由6个同样大小的正方体摆成的几何体,在正方体①的正上方再放一个这样的正方体,所得的几何体( )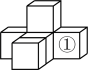 A、主视图改变,左视图不变 B、俯视图改变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图改变
A、主视图改变,左视图不变 B、俯视图改变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图改变二、填空题
-
11. 一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图所示,则搭成这个几何体的小立方块最多有个.
 12. 如图是某风力发电机示意图,其相同的三个叶片均匀分布,每个叶片长 , 即水平地面上的点在旋转中心的正下方 , 即当风力发电机叶片外端点离地面的高度最大时,若垂直于地面的木棒与影长的比为: , 则此刻风力发电机的影长为
12. 如图是某风力发电机示意图,其相同的三个叶片均匀分布,每个叶片长 , 即水平地面上的点在旋转中心的正下方 , 即当风力发电机叶片外端点离地面的高度最大时,若垂直于地面的木棒与影长的比为: , 则此刻风力发电机的影长为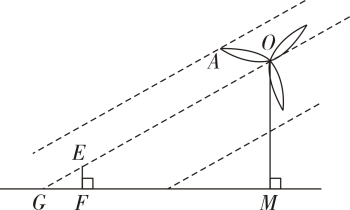 13. 某几何体的三视图如图所示,根据图中数据可得,该几何体的侧面积为 .
13. 某几何体的三视图如图所示,根据图中数据可得,该几何体的侧面积为 . 14. 某机器零件的尺寸标注如图所示,在其主视图,左视图和俯视图中,既是轴对称图形又是中心对称图形的是 .
14. 某机器零件的尺寸标注如图所示,在其主视图,左视图和俯视图中,既是轴对称图形又是中心对称图形的是 .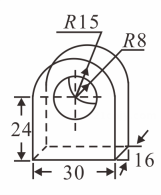 15. 如图,已知圆锥的底面圆半径为l,则该圆锥的俯视图的面积为 .
15. 如图,已知圆锥的底面圆半径为l,则该圆锥的俯视图的面积为 .
三、作图题
-
16. 画出如图所示的立体图形的三视图.
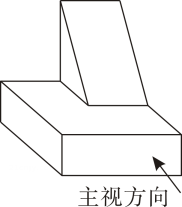 17. 把边长为1的10个相同的正方体摆成如图的形式,画出该几何体的主视图、左视图、俯视图.
17. 把边长为1的10个相同的正方体摆成如图的形式,画出该几何体的主视图、左视图、俯视图.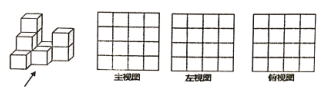
四、解答题
-
18. 某小组的项目式学习活动内容是测量某棵古树的高度 , 如图,在阳光下,某一时刻,古树的影子落在了地上和围墙上,落在地上的长度米,落在墙上的长度米,在古树的附近有一棵小树 , 同一时刻,小树的影长米,小树的高米.已知点N,P,B,D在一条水平线上, , , , 请求出该古树的高度 .
 19. “创新实践”小组想利用所学知识测量大树的高度,因大树底部有障碍物,无法直接测量到大树底部的距离,他们制定了如下的测量方案:如图所示,小丽通过调整测角仪的位置,在大树周围的点C处用测角仪测得大树顶部A的仰角为(测角仪的高度忽略不计).接着,小丽沿着方向向前走3米(即米),到达大树在太阳光下的影子末端D处,此时小明测得小丽在太阳光下的影长为2米.已知小丽的身高为1.5米,B、C、D、F四点在同一直线上, , 求这棵大树的高度.
19. “创新实践”小组想利用所学知识测量大树的高度,因大树底部有障碍物,无法直接测量到大树底部的距离,他们制定了如下的测量方案:如图所示,小丽通过调整测角仪的位置,在大树周围的点C处用测角仪测得大树顶部A的仰角为(测角仪的高度忽略不计).接着,小丽沿着方向向前走3米(即米),到达大树在太阳光下的影子末端D处,此时小明测得小丽在太阳光下的影长为2米.已知小丽的身高为1.5米,B、C、D、F四点在同一直线上, , 求这棵大树的高度.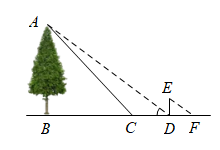
五、实践探究题
-
20. 【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
 (1)、【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
(1)、【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程已知:如图1,在Rt△ABC中,∠C=90°,∠A=30°.
求证:BC= AB.
(2)、【灵活运用】该同学家有一张折叠方桌如图2①所示,方桌的主视图如图2②.经测得OA=OB=90cm,OC=OD=30cm,将桌子放平,两条桌腿叉开的角度∠AOB=120°.求:桌面与地面的高度.六、综合题
-
21. 两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到;玉壁,玉环为我国的传统玉器,通常为正中带圆孔的扇圆型器物,据《尔雅·释器》记载:“肉倍好,谓之璧;肉好若一,调之环.”如图1,“肉”指边(阴影部分),“好”指孔,其比例关系见图示,以考古发现看,这两种玉器的“肉”与“好”未必符合该比例关系.
 (1)、若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为;(2)、利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法).
(1)、若图1中两个大圆的直径相等,则璧与环的“肉”的面积之比为;(2)、利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法).①图2为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”?
②图3表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
-

