吉林省松原市乾安县2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-03-05 类型：期末考试

进入出卷网下载

一、单项选择题

1. 下列函数中，y是x的反比例函数的是（　　）

A、 $y = 3 x$ B、 $y = \frac{3}{x}$ C、 $y = \frac{x^{2}}{3}$ D、 $y = \frac{3}{x + 1}$

查看试题解析
2. 抛物线 $y = (x + 1)^{2} + 2$ 的对称轴是（）

A、直线 $x = 1$ B、直线 $x = - 1$ C、直线 $x = 2$ D、直线 $x = - 2$

查看试题解析
3. 围棋起源于中国，古代称之为“弈”，至今已有 $4000$ 多年的历史． $2017$ 年 $5$ 月，世界围棋冠军柯洁与人工智能机器人 $A l p h a G o$ 进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，点A，B，C是⊙O上的点，∠AOB=70°，则∠ACB的度数是（）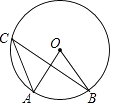

A、30° B、35° C、45° D、70°

查看试题解析
5. 如图，香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合，则n的最小值为（）

A、45 B、60 C、72 D、144

查看试题解析
6. 如图，电路图上有4个开关A、B、C、D和1个小灯泡，在所有的元件和线路都正常的前提下．下列操作中，“小灯泡发光”这个事件是不可能事件的是（）

A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关

查看试题解析

二、填空题

7. 写出一个二次函数，其图象满足：①开口向下；②与y轴交于点（0，2），这个二次函数的解析式可以是．

查看试题解析
8. 若点 $A (3 ， 8)$ 在一个反比例函数的图象上，则这个反比例函数的解析式为．

查看试题解析
9. 小军与小王一起玩“石头、剪刀、布”的游戏，两同学同时出“石头”的概率是．

查看试题解析
10. 已知 $- 1$ 是关于 $x$ 的一元二次方程 $x^{2} + k x - 3 = 0$ 的一个根，则 $k =$

查看试题解析
11. 参加一次活动的每个人都和其他人各握了一次手，所有人共握手10次，有多少人参加活动？设有 $x$ 人参加活动，可列方程为

查看试题解析
12. 如图，⊙O 的半径为1，PA，PB是⊙O的两条切线，切点分别为A，B．连接OA，OB，AB，PO，若∠APB=60°，则△PAB的周长为．

查看试题解析
13. 已知二次函数 $y_{1} = a x^{2} + b x + c (a \neq 0)$ 和一次函数 $y_{2} = k x + n (k \neq 0)$ 的图象如图所示，下面有四个推断：
①二次函数 $y_{1}$ 有最大值
②二次函数 $y_{1}$ 的图象关于直线 $x = - 1$ 对称
③当 $x = - 2$ 时，二次函数 $y_{1}$ 的值大于0
④过动点 $P (m ， 0)$ 且垂直于x轴的直线与 $y_{1} ， y_{2}$ 的图象的交点分别为C，D当点C位于点D上方时，m的取值范围是 $m < - 3$ 或 $m > - 1$
其中正确的是.

查看试题解析
14. 如图，在平面直角坐标系 $x O y$ 中，等边 $△ A B C$ 的顶点A在y轴的正半轴上， $B (- 5 ， 0)$ ， $C (5 ， 0)$ ，点 $D (11 ， 0)$ ，将 $△ A C D$ 绕点A顺时针旋转 $60 °$ 得到 $△ A B E$ ，则 $\overset{⌢}{B C}$ 的长度为．

查看试题解析

三、解答题

15. 解关于x的方程： $x^{2} + 3 x + 2 = 0$

查看试题解析
16. 孟浩然是唐代著名的山水田园派诗人．《春晓》是他创作的一首名篇，这首古诗共有四句，如图，将这四句古诗分别制成编号为A，B，C，D的4张卡片，卡片除编号和内容外，其余完全相同．将这4张卡片背面朝上，洗匀放好．现从4张卡片中随机抽取2张，请用列表或画树状图的方法，求出随机抽出2张卡片恰好为相邻两句古诗的概率．

查看试题解析
17. 已知关于x的一元二次方程 $x^{2} - (m + 3) x + m + 2 = 0$ .

(1)、求证：方程总有两个实数根；

(2)、若方程两个根的绝对值相等，求此时m的值.

查看试题解析
18. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点H， $∠ A = 30 °$ ， $C D = 2 \sqrt{3}$ ，求 $⊙ O$ 的半径的长．

查看试题解析
19. 下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程．
已知：如图，⊙O及⊙O上一点P．
求作：过点P的⊙O的切线．
作法：如图，作射线OP；
① 在直线OP外任取一点A，以A为圆心，AP为半径作⊙A，与射线OP交于另一点B；
②连接并延长BA与⊙A交于点C；
③作直线PC；
则直线PC即为所求．根据小元设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；（保留作图痕迹）

(2)、完成下面的证明：
证明：∵ BC是⊙A的直径，
∴ ∠BPC=90°（）（填推理依据）．
∴ OP⊥PC．
又∵ OP是⊙O的半径，
∴ PC是⊙O的切线（）（填推理依据）．

查看试题解析
20. 如图，根据小孔成像的科学原理，当像距 $($ 小孔到像的距离 $)$ 和物高 $($ 蜡烛火焰高度 $)$ 不变时，火焰的像高 $y ($ 单位： $c m)$ 是物距 $($ 小孔到蜡烛的距离 $) x ($ 单位： $c m)$ 的反比例函数，当 $x = 6$ 时， $y = 2$ ．

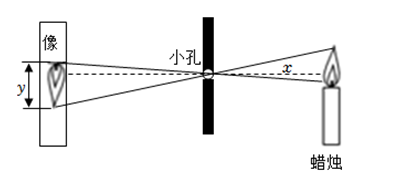(1)、求 $y$ 关于 $x$ 的函数解析式．

(2)、若火焰的像高为 $3 c m$ ，求小孔到蜡烛的距离．

查看试题解析
21. 如图①，在 $R t △ A B C$ 中， $∠ C = 90 °$ ．将 $△ A B C$ 绕点C逆时针旋转得到 $△ A^{'} B^{'} C^{'}$ ，旋转角为α，且 $0 ° < α < 180 °$ ，在旋转过程中，点B可以恰好落在 $A B$ 的中点处，如图②．求 $∠ A$ 的度数．

查看试题解析
22. 某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件；每降价1元，每星期可多卖出20件．已知商品的进价为每件40元，如何定价才能使得利润最大？
小明同学，为了完成以上问题，小明分析：调整价格包括涨价和降价两种情况．小明先探索了涨价的情况，下面是小明的思路，请你帮助小明完善以下内容：

(1)、假设每件涨价x元，则所得利润y与x的函数关系式为；其中x的取值范围是；在涨价的情况下，定价元时，利润最大，最大利润是．

(2)、请你参考小明（1）的思路继续思考，在降价的情况下，求最大利润是多少？

(3)、在（1）（2）的讨论及现在的销售情况，回答商家如何定价能使利润能达到最大？

查看试题解析
23. 体育测试时，九年级一名学生，双手扔实心球．已知实心球所经过的路线是某个二次函数图象的一部分，如果球出手处 $A$ 点距离地面的高度为 $2 m$ ，当球运行的水平距离为 $4 m$ 时，达到最大高度 $4 m$ 的 $B$ 处（如图），问该学生把实心球扔出多远？（结果保留根号）

查看试题解析
24. 如图1是实验室中的一种摆动装置， $B C$ 在地面上，支架 $A B C$ 是底边为 $B C$ 的等腰直角三角形，摆动臂长 $A D$ 可绕点A旋转，摆动臂 $D M$ 可绕点D旋转， $A D = 30$ ， $D M = 10$ .

(1)、在旋转过程中：
①当 $A ， D ， M$ 三点在同一直线上时，求 $A M$ 的长；

②当 $A ， D ， M$ 三点在同一直角三角形的顶点时，求 $A M$ 的长.

(2)、若摆动臂 $A D$ 顺时针旋转 $90 °$ ，点 $D$ 的位置由 $△ A B C$ 外的点 $D_{1}$ 转到其内的点 $D_{2}$ 处，连结 $D_{1} D_{2}$ ，如图2，此时 $∠ A D_{2} C = 135 °$ ， $C D_{2} = 60$ ，求 $B D_{2}$ 的长.

查看试题解析
25. 如图，在正方形 $A B C D$ 中， $A B = 4 c m$ ，点O是对角线 $A C$ 的中点，动点P、Q分别从点A，B同时出发，点P以 $1 c m / s$ 的速度沿边 $A B$ 向终点B匀速运动，点Q以 $2 c m / s$ 的速度沿折线 $B C - C D$ 向终点D匀速运动，连接 $P O$ 并延长交边 $C D$ 于点 $M$ ，连接 $Q O$ 并延长交折线 $D A - A B$ 于点N，连接 $P Q$ ， $Q M$ ， $M N$ ， $N P$ ，得到四边形 $P Q M N$ ．设点P的运动时间为 $x (s) (0 < x < 4)$ ，四边形 $P Q M N$ 的面积为 $y (c m^{2})$ ．

(1)、 $B P$ 的长为 $c m$ ， $C M$ 的长为 $c m$ ．（用含x的代数式表示）

(2)、求y关于x的函数解析式，并写出自变量x的取值范围．

查看试题解析
26. 阅读理解：
某“数学兴趣小组”根据学习函数的经验，对函数 $y = - x^{2} + 2 | x | + 1$ 的图象和性质进行了探究，探究过程如下，请补充完整：

(1)、自变量x的取值范围是全体实数，x与y的几组对应数值如下表：
$x$
…
$- 3$
$- \frac{5}{2}$
$\begin{array}{l} - 2 \end{array}$
$- 1$
$0$
$1$
$2$
$\frac{5}{2}$
$3$
…
$y$
…
$\begin{array}{l} - 2 \end{array}$
$- \frac{1}{4}$
$m$
$2$
$1$
$2$
$1$
$- \frac{1}{4}$
$\begin{array}{l} - 2 \end{array}$
…
其中 $m =$ ；

(2)、在平面直角坐标系 $x O y$ 中，描出以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

(3)、根据函数图象，回答下列问题：
①当 $- 1 \leq x < 1$ 时，则y的取值范围为．
②直线 $y = k x + b$ 经过点 $(1 ， 2)$ ，若关于x的方程 $- x^{2} + 2 | x | + 1 = k x + b$ 有4个互不相等的实数根，则b的取值范围是．

查看试题解析

$x$	…	$- 3$	$- \frac{5}{2}$	$\begin{array}{l} - 2 \end{array}$	$- 1$	$0$	$1$	$2$	$\frac{5}{2}$	$3$	…
$y$	…	$\begin{array}{l} - 2 \end{array}$	$- \frac{1}{4}$	$m$	$2$	$1$	$2$	$1$	$- \frac{1}{4}$	$\begin{array}{l} - 2 \end{array}$	…