吉林省长春市德惠市2023-2024学年九年级上学期期末数学试卷
试卷更新日期:2024-03-05 类型:期末考试
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列式子中是最简二次根式的是( )A、 B、 C、 D、2. 若 , 则下列比例式正确的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、“买中奖率为的奖券张,一定中奖”是必然事件 B、“汽车累积行驶 , 从未出现故障”是不可能事件 C、天气预报说“明天的降水概率为”,意味着明天一定下雨 D、“清明时节雨纷纷”为随机事件4. 下列各式计算正确的是( )A、 B、 C、 D、5. 如图是一架人字梯,已知 , 两梯脚之间的距离米,与地面的夹角为 , 则人字梯长为( )
 A、米 B、米 C、米 D、米6. 如图,的三个顶点都在方格纸的格点上,其中点的坐标是 , 现将绕点按逆时针方向旋转 , 则旋转后点的坐标是( )
A、米 B、米 C、米 D、米6. 如图,的三个顶点都在方格纸的格点上,其中点的坐标是 , 现将绕点按逆时针方向旋转 , 则旋转后点的坐标是( ) A、 B、 C、 D、7. 若关于的一元二次方程的两个实数根分别为 , , 那么抛物线的对称轴为直线( )A、 B、 C、 D、8. 在年中考体育考试前,小康对自己某次实心球的训练录像进行了分析,发现实心球飞行路线是一条抛物线,若不考虑空气阻力,实心球的飞行高度单位:米与飞行的水平距离单位:米之间具有函数关系 , 则小康这次实心球训练的成绩为( )
A、 B、 C、 D、7. 若关于的一元二次方程的两个实数根分别为 , , 那么抛物线的对称轴为直线( )A、 B、 C、 D、8. 在年中考体育考试前,小康对自己某次实心球的训练录像进行了分析,发现实心球飞行路线是一条抛物线,若不考虑空气阻力,实心球的飞行高度单位:米与飞行的水平距离单位:米之间具有函数关系 , 则小康这次实心球训练的成绩为( ) A、米 B、米 C、米 D、米
A、米 B、米 C、米 D、米二、填空题:本题共6小题,每小题3分,共18分。
-
9. 函数y= 的自变量x的取值范围是.10. 一个盒子中有m个红球、3个白球,每个球除颜色外都相同.从中任取一个球,若取得白球的概率是则m= .11. 若关于的一元二次方程有两个相等的实数根,则 .12. 和的三边长分别为、、和、、 , 且两三角形相似,则与的面积比为 .13. 如图,矩形中, , E是上一点,与交于点F.则的长为 .
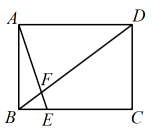 14. 如图,用长为的篱笆,一边利用墙墙足够长围成一个长方形花园,设花园的宽为 , 围成的花圃面积为 , 则关于的函数表达式为 .
14. 如图,用长为的篱笆,一边利用墙墙足够长围成一个长方形花园,设花园的宽为 , 围成的花圃面积为 , 则关于的函数表达式为 .
三、解答题:本题共10小题,共78分。解答应写出文字说明,证明过程或演算步骤。
-
15. 计算: .16. 解方程: .17. 不透明的袋子中装有个红球和个白球,这些球除颜色外完全相同若从袋子中随机摸出个球,请用列表或画树状图的方法,求摸出的个球颜色不同的概率.18. 建设美丽城市,改造老旧小区.某市年投入资金万元,年投入资金万元,现假定每年投入资金的增长率相同.求该市改造老旧小区投入资金的年平均增长率.19. 如图, , 直线 , 交于点 , 且分别与直线 , , 交于点、、和点、、 , 已知 , , , , 求的长度是?
 20. 图、图、图均是的正方形网格,每个小正方、、均在格点上请按要求完成作图,保留作图痕迹.
20. 图、图、图均是的正方形网格,每个小正方、、均在格点上请按要求完成作图,保留作图痕迹. (1)、在线段上找一点 , 使其平分线段;(2)、在线段上找一点 , 使其分线段为:两部分;(3)、在线段上找一点 , 使 .21. 2022年11月29日,搭载神舟十五号载人飞船的运载火箭在酒泉卫星发射中心成功发射.运载火箭从发射点O处发射,当火箭到达A处时、在地面雷达站C处测得点A的仰角为 , 在地面雷达站B处测得点A的仰角为 . 已知 , O、B、C三点在同一条直线上,求B、C两个雷达站之间的距离(结果精确到 , 参考数据).
(1)、在线段上找一点 , 使其平分线段;(2)、在线段上找一点 , 使其分线段为:两部分;(3)、在线段上找一点 , 使 .21. 2022年11月29日,搭载神舟十五号载人飞船的运载火箭在酒泉卫星发射中心成功发射.运载火箭从发射点O处发射,当火箭到达A处时、在地面雷达站C处测得点A的仰角为 , 在地面雷达站B处测得点A的仰角为 . 已知 , O、B、C三点在同一条直线上,求B、C两个雷达站之间的距离(结果精确到 , 参考数据). 22. 【教材呈现】如图是华师版九年级上册数学教材第页的部分内容.
22. 【教材呈现】如图是华师版九年级上册数学教材第页的部分内容.猜想:如图,在中,点、分别是与的中点根据画出的图形,可以猜想:
, 且
对此,我们可以用演绎推理给出证明.

 (1)、【定理证明】请根据教材内容,结合图 , 写出证明过程.(2)、【定理应用】如图 , 已知矩形中, , , 点在上从向移动,、、分别是、、的中点,则 .(3)、【拓展提升】如图 , 中, , , 点 , 分别是 , 的中点,点在上,且 , 则 .23. 如图,在平面直角坐标系中,抛物线与轴相交于点 .
(1)、【定理证明】请根据教材内容,结合图 , 写出证明过程.(2)、【定理应用】如图 , 已知矩形中, , , 点在上从向移动,、、分别是、、的中点,则 .(3)、【拓展提升】如图 , 中, , , 点 , 分别是 , 的中点,点在上,且 , 则 .23. 如图,在平面直角坐标系中,抛物线与轴相交于点 . (1)、求的值;(2)、点为轴上一点,其纵坐标为 , 连接 , 以为边向右作正方形 .
(1)、求的值;(2)、点为轴上一点,其纵坐标为 , 连接 , 以为边向右作正方形 .设抛物线的顶点为 , 当点在上时,求的值;
当点在抛物线上时,求的值;
当抛物线与正方形有两个交点时,直接写出的取值范围.
24. 如图,中, , , 点从点出发沿折线以每秒个单位长的速度向点匀速运动,点从点出发沿以每秒个单位长的速度向点匀速运动,点、同时出发,当其中一点到达点时停止运动,另一点也随之停止设点、运动的时间是秒 .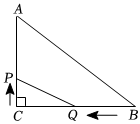 (1)、当时, ;当时, .(2)、当点、重合时,求出的长.(3)、点、分别在、上时,的面积能否是面积的一半?若能,求出的值;若不能,请说明理由.(4)、当与的一边平行时,直接写出的值.
(1)、当时, ;当时, .(2)、当点、重合时,求出的长.(3)、点、分别在、上时,的面积能否是面积的一半?若能,求出的值;若不能,请说明理由.(4)、当与的一边平行时,直接写出的值.