吉林省松原市前郭县2023-2024学年九年级上学期期末数学试卷
试卷更新日期:2024-03-05 类型:期末考试
一、选择题:本题共6小题,每小题2分,共12分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 年冬奥会会徽和冬残奥会会徽部分作品图中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列关于的方程中,一定是一元二次方程的为( ).A、 B、 C、 D、3. 若函数是反比例函数,则的值为( )A、 B、 C、或 D、4. 下列属于随机事件的是( )A、一个袋中有个红球,从中摸出一个球是红球 B、两条直线被第三条直线所截,同位角相等 C、在地球上,抛出的篮球会落下 D、从装有个白球的不透明袋中取出个黑球5. 如图,在中,若 , , 则扇形(阴影部分)的面积是( )
2. 下列关于的方程中,一定是一元二次方程的为( ).A、 B、 C、 D、3. 若函数是反比例函数,则的值为( )A、 B、 C、或 D、4. 下列属于随机事件的是( )A、一个袋中有个红球,从中摸出一个球是红球 B、两条直线被第三条直线所截,同位角相等 C、在地球上,抛出的篮球会落下 D、从装有个白球的不透明袋中取出个黑球5. 如图,在中,若 , , 则扇形(阴影部分)的面积是( ) A、 B、 C、 D、6. 如图,二次函数的图象经过点 , 对称轴是直线 , 如果你不知道下列结论: , , , 中,哪些是正确结论,那么你从中随机选择一个结论是正确的概率是( )
A、 B、 C、 D、6. 如图,二次函数的图象经过点 , 对称轴是直线 , 如果你不知道下列结论: , , , 中,哪些是正确结论,那么你从中随机选择一个结论是正确的概率是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共8小题,每小题3分,共24分。
-
7. 已知是方程的一个根,则式子的值为 .8. 抛物线向右平移个单位,向上平移个单位后经过点则的值是 .9. 已知、两点关于原点对称,则 .10. 在一个不透明的盒子中有25个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后,发现摸到白球的频率稳定于0.4,由此可估计盒子中白球的个数约为 .11. 如图,点是反比例函数的图象上的一点,点在轴的负半轴上且 , 若的面积为 , 则的值为 .
 12. 二次函数的部分图象如图所示,则方程的根为 .
12. 二次函数的部分图象如图所示,则方程的根为 . 13. 在九章算术中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为寸,锯道尺尺寸 , 则该圆材的直径为寸.
13. 在九章算术中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为寸,锯道尺尺寸 , 则该圆材的直径为寸. 14. 如图,一次函数的图象与反比例函数的图象交于 , 两点,则不等式的解集为 .
14. 如图,一次函数的图象与反比例函数的图象交于 , 两点,则不等式的解集为 .
三、计算题:本大题共1小题,共5分。
-
15. 解方程:x2-2x-1=0.
四、解答题:本题共11小题,共79分。解答应写出文字说明,证明过程或演算步骤。
-
16. 如图,方格纸中的每个小正方形的边长都是 , 小正方形的顶点称作格点,的三个顶点都在格点上,把先向右平移个单位,再向下平移个单位得 , 再将绕点顺时针旋转得结合所给的平面直角坐标系,回答下列问题:
 (1)、在平面直角坐标系中画出和;(2)、图中的能不能通过顺时针旋转得到?如果可以,请写出旋转中心的坐标及旋转角的度数;如果不能,说明理由.17. 如图, , 是的两条弦,且 , , D为弦所对优弧上一点,求的度数.
(1)、在平面直角坐标系中画出和;(2)、图中的能不能通过顺时针旋转得到?如果可以,请写出旋转中心的坐标及旋转角的度数;如果不能,说明理由.17. 如图, , 是的两条弦,且 , , D为弦所对优弧上一点,求的度数. 18. 已知反比例函数的图象经过第一、三象限.(1)、求的取值范围;(2)、若 , 此函数的图象过第一象限的两点 , 且 , 求的取值范围.19. 二十四节气是中国古代一种用来指导农事的补充历法,在国际气象界被誉为“中国的第五大发明”,并位列联合国教科文组织人类非物质文化遗产代表作名录,小明和小亮对二十四节气非常感兴趣,在课间玩游戏时,准备了四张完全相同的不透明卡片,卡片正面分别写有“惊蛰”“夏至”“白露”“霜降”四个节气,两人商量将卡片背面朝上洗匀后,从中随机抽取一张,并讲述所抽卡片上的节气的由来与习俗.(1)、小明从四张卡片中随机抽取一张卡片,抽到“惊蛰”的概率是 .(2)、小明先从四张卡片中随机抽取一张,小亮再从剩下的卡片中随机抽取一张,请用列表或画树状图的方法,求两人都没有抽到“夏至”的概率.20. 如图,是的角平分线,点是上一点,与相切于点 , 与交于点、 .
18. 已知反比例函数的图象经过第一、三象限.(1)、求的取值范围;(2)、若 , 此函数的图象过第一象限的两点 , 且 , 求的取值范围.19. 二十四节气是中国古代一种用来指导农事的补充历法,在国际气象界被誉为“中国的第五大发明”,并位列联合国教科文组织人类非物质文化遗产代表作名录,小明和小亮对二十四节气非常感兴趣,在课间玩游戏时,准备了四张完全相同的不透明卡片,卡片正面分别写有“惊蛰”“夏至”“白露”“霜降”四个节气,两人商量将卡片背面朝上洗匀后,从中随机抽取一张,并讲述所抽卡片上的节气的由来与习俗.(1)、小明从四张卡片中随机抽取一张卡片,抽到“惊蛰”的概率是 .(2)、小明先从四张卡片中随机抽取一张,小亮再从剩下的卡片中随机抽取一张,请用列表或画树状图的方法,求两人都没有抽到“夏至”的概率.20. 如图,是的角平分线,点是上一点,与相切于点 , 与交于点、 . (1)、求证:是的切线;(2)、连接 , 若 , 求的度数.21. 关于的一元二次方程有两个实数根.(1)、求的取值范围;(2)、上述方程的根 , 恰好是斜边为的直角三角形另外两边的边长,求这个三角形的周长.22. 驾驶员血液中每毫升的酒精含量大于或等于微克即为酒驾,某研究所经实验测得,成人饮用某品牌度白酒后血液中酒精浓度微克毫升与饮酒时间小时之间函数关系如图所示当时,与成反比例 .
(1)、求证:是的切线;(2)、连接 , 若 , 求的度数.21. 关于的一元二次方程有两个实数根.(1)、求的取值范围;(2)、上述方程的根 , 恰好是斜边为的直角三角形另外两边的边长,求这个三角形的周长.22. 驾驶员血液中每毫升的酒精含量大于或等于微克即为酒驾,某研究所经实验测得,成人饮用某品牌度白酒后血液中酒精浓度微克毫升与饮酒时间小时之间函数关系如图所示当时,与成反比例 .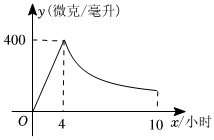 (1)、根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为 ;下降阶段的函数解析式为 ;并写出的取值范围(2)、问血液中酒精浓度不低于微克毫升的持续时间是多少小时?23. 某超市以每千克元的价格购进一种干果,计划以每千克元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种干果销售量千克与每千克降价元之间满足一次函数关系,其图象如图所示.
(1)、根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为 ;下降阶段的函数解析式为 ;并写出的取值范围(2)、问血液中酒精浓度不低于微克毫升的持续时间是多少小时?23. 某超市以每千克元的价格购进一种干果,计划以每千克元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种干果销售量千克与每千克降价元之间满足一次函数关系,其图象如图所示. (1)、求与之间的函数关系式;(2)、当每千克干果降价元时,超市获利多少元?(3)、若超市要想获利元,且让顾客获得更大实惠,这种干果每千克应降价多少元?24. 问题情境:在学习图形的平移和旋转时,数学兴趣小组遇到这样一个问题:如图 , 点为等边的边上一点,将线段绕点逆时针旋转得到线段 , 连接 .
(1)、求与之间的函数关系式;(2)、当每千克干果降价元时,超市获利多少元?(3)、若超市要想获利元,且让顾客获得更大实惠,这种干果每千克应降价多少元?24. 问题情境:在学习图形的平移和旋转时,数学兴趣小组遇到这样一个问题:如图 , 点为等边的边上一点,将线段绕点逆时针旋转得到线段 , 连接 .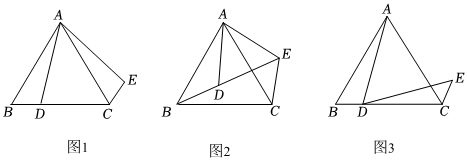 (1)、【猜想证明】试猜想与的数量关系,并加以证明;(2)、【探究应用】如图 , 点为等边内一点,将线段绕点逆时针旋转得到线段 , 连接 , 若、、三点共线,求证:平分;(3)、【拓展提升】如图 , 若是边长为的等边三角形,点是线段上的动点,将线段绕点顺时针旋转得到线段 , 连接点在运动过程中,的周长最小值直接写答案 .25. 在平面直角坐标系中,为原点,是等腰直角三角形, , , 顶点 , 点在第一象限,矩形的顶点 , , 点在第二象限将矩形沿轴向右平移,得到矩形 , 点 , , , 的对应点分别为 , , , 设 .
(1)、【猜想证明】试猜想与的数量关系,并加以证明;(2)、【探究应用】如图 , 点为等边内一点,将线段绕点逆时针旋转得到线段 , 连接 , 若、、三点共线,求证:平分;(3)、【拓展提升】如图 , 若是边长为的等边三角形,点是线段上的动点,将线段绕点顺时针旋转得到线段 , 连接点在运动过程中,的周长最小值直接写答案 .25. 在平面直角坐标系中,为原点,是等腰直角三角形, , , 顶点 , 点在第一象限,矩形的顶点 , , 点在第二象限将矩形沿轴向右平移,得到矩形 , 点 , , , 的对应点分别为 , , , 设 . (1)、如图 , 当时,与交于点,求点 , 的坐标;(2)、若矩形与重叠部分的面积为 .
(1)、如图 , 当时,与交于点,求点 , 的坐标;(2)、若矩形与重叠部分的面积为 .如图 , 当矩形与重叠部分为五边形时,分别与交于点 , 与交于点与交于点 , 试用含有的式子表示 , 并直接写出的取值范围;
当时,求的取值范围直接写出结果即可 .
26. 如图,在平面直角坐标系中,二次函数的图象与轴交于 , 点,与轴交于点 , 点在原点的左侧,点的坐标为 , 点是抛物线上一个动点,且在直线的上方. (1)、求这个二次函数的解析式;(2)、当点运动到什么位置时,的面积最大?请求出点的坐标和面积的最大值.(3)、连接 , , 并把沿翻折,得到四边形 , 那么是否存在点 , 使四边形为菱形?若存在,请求出此时点的坐标;若不存在,请说明理由.
(1)、求这个二次函数的解析式;(2)、当点运动到什么位置时,的面积最大?请求出点的坐标和面积的最大值.(3)、连接 , , 并把沿翻折,得到四边形 , 那么是否存在点 , 使四边形为菱形?若存在,请求出此时点的坐标;若不存在,请说明理由.
-