吉林省长春市九台区2023-2024学年七年级上学期期末数学试卷
试卷更新日期:2024-03-05 类型:期末考试
一、选择题(本大题共8道题,每题3分,共24分)
-
1. 如图,在数轴上点M表示的数可能是( )
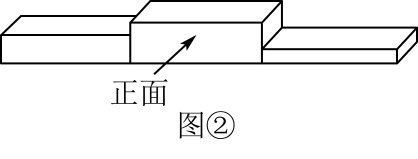
 A、1.5 B、﹣1.5 C、﹣2.5 D、2.52. 下列说法正确的是( )A、延长射线OA B、延长直线AB C、延长线段AB D、作直线AB=CD3. 图①是2023年6月11日吉林市全程马拉松男子组颁奖现场.图②是领奖台的示意图,则此领奖台的主视图是( )
A、1.5 B、﹣1.5 C、﹣2.5 D、2.52. 下列说法正确的是( )A、延长射线OA B、延长直线AB C、延长线段AB D、作直线AB=CD3. 图①是2023年6月11日吉林市全程马拉松男子组颁奖现场.图②是领奖台的示意图,则此领奖台的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、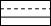 4. 多项式x2y3﹣3xy3﹣2的次数和项数分别为( )A、5,3 B、5,2 C、2,3 D、3,35. 把一条弯曲的公路改成直道,可以缩短路程,其道理用几何的知识解释应是( )
4. 多项式x2y3﹣3xy3﹣2的次数和项数分别为( )A、5,3 B、5,2 C、2,3 D、3,35. 把一条弯曲的公路改成直道,可以缩短路程,其道理用几何的知识解释应是( )
A、两点确定一条直线 B、两点之间线段最短 C、线段有两个端点 D、线段可比较大小6. 为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )A、8x元 B、10(100﹣x)元 C、8(100﹣x)元 D、(100﹣8x)元7. 如图,OA是北偏东30°方向的一条射线,OB是北偏西50°方向的一条射线,那么∠AOB的大小为( ) A、70° B、80° C、100° D、110°8. 如图,将木条a,b与c钉在一起,∠1=85°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A、70° B、80° C、100° D、110°8. 如图,将木条a,b与c钉在一起,∠1=85°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( ) A、50° B、35° C、25° D、15°
A、50° B、35° C、25° D、15°二、填空题(本大题共6道题,每题3分,共18分)
-
9. 将多项式3x2﹣1﹣6x5﹣4x3按字母x的降幂排列为 .10. 用四舍五入法取近似值为3.31,那么这个数精确到 位.11. 已知单项式的系数为m,次数为n,则mn的值为 .12. 已知a﹣b=3,c+d=2,则(a+c)﹣(b﹣d)的值为 .13. 如图是一个多面体的表面展开图,每个面都标注了数字.若多面体的底面是面③,则多面体的上面是面 . (填数字序号)
 14. 如图,运动会上,小明自踏板M处跳到沙坑P处,甲、乙、丙三名同学分别测得PM=3.25米,PN=3.15米,PF=3.21米,则小明的成绩为 米.(填具体数值)
14. 如图,运动会上,小明自踏板M处跳到沙坑P处,甲、乙、丙三名同学分别测得PM=3.25米,PN=3.15米,PF=3.21米,则小明的成绩为 米.(填具体数值)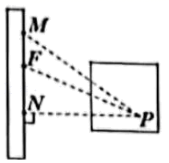
三、解答题(本大题共78分)
-
15. 计算:(1)、 ;(2)、.16. 计算:(1)、34°26'﹣25°33';(2)、5m2﹣(m2﹣6m)﹣2(﹣m+3m2).17. 如图,在6×6的正方形网格中,每个小正方形的边长均为1,其顶点称为格点,点A、B、C、D均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
 (1)、画直线AB、射线BC;(2)、画线段CD,在线段CD上确定一点E,使DE=3CE;(3)、过点A画垂线段AF⊥CD,垂足为F.18. 嘉淇准备完成题目:化简:(□x2+6x+8)﹣(6x+5x2+2),发现系数“□”印刷不清楚.(1)、他把“□”猜成3,请你化简:(3x2+6x+8)﹣(6x+5x2+2);(2)、他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“□”是几?19. 如图,点C是线段AB的中点,点D是线段BC的中点,AB=8.
(1)、画直线AB、射线BC;(2)、画线段CD,在线段CD上确定一点E,使DE=3CE;(3)、过点A画垂线段AF⊥CD,垂足为F.18. 嘉淇准备完成题目:化简:(□x2+6x+8)﹣(6x+5x2+2),发现系数“□”印刷不清楚.(1)、他把“□”猜成3,请你化简:(3x2+6x+8)﹣(6x+5x2+2);(2)、他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“□”是几?19. 如图,点C是线段AB的中点,点D是线段BC的中点,AB=8. (1)、求线段AD的长.(2)、若点E是线段AB上一点,CE=BC,求线段AE的长.20. 如图,直线AB与CD相交于点F,EF⊥AB于点F.
(1)、求线段AD的长.(2)、若点E是线段AB上一点,CE=BC,求线段AE的长.20. 如图,直线AB与CD相交于点F,EF⊥AB于点F. (1)、图中与∠1相等的角是 , 与∠1互余的角是 ;(2)、若∠AFD=155°,求∠DFE的度数.21.(1)、若一个三位数的百位、十位和个位上的数字分别为x,y和z,则这个三位数可记为 , 易得=100x+10y+z.(1)如果要用数字3、7、9组成一个三位数(各数位上的数不同),那么组成的数中最大的三位数是 , 最小的三位数是 .(2)、若一个三位数各数位上的数由a,b,c三个数字组成,且a>b>c>0.那么,请说明所组成的最大三位数与最小三位数之差可以被99整除.22. 如图,学校要利用专款建一长方形的自行车停车场,其他三面用护栏围起,其中长方形停车场的长为(2a+3b)米,宽比长少(a﹣b)米.
(1)、图中与∠1相等的角是 , 与∠1互余的角是 ;(2)、若∠AFD=155°,求∠DFE的度数.21.(1)、若一个三位数的百位、十位和个位上的数字分别为x,y和z,则这个三位数可记为 , 易得=100x+10y+z.(1)如果要用数字3、7、9组成一个三位数(各数位上的数不同),那么组成的数中最大的三位数是 , 最小的三位数是 .(2)、若一个三位数各数位上的数由a,b,c三个数字组成,且a>b>c>0.那么,请说明所组成的最大三位数与最小三位数之差可以被99整除.22. 如图,学校要利用专款建一长方形的自行车停车场,其他三面用护栏围起,其中长方形停车场的长为(2a+3b)米,宽比长少(a﹣b)米. (1)、用a、b表示长方形停车场的宽;(2)、求护栏的总长度;(3)、若a=30,b=10,每米护栏造价80元,求建此停车场所需的费用.23. 【教材呈现】如图是华师版七年级上册数学教材第176页的部分内容.有了“两直线平行,同位角相等”,我们就能用推理的方法得出“两条平行线被第三条直线所截,内错角相等”.
(1)、用a、b表示长方形停车场的宽;(2)、求护栏的总长度;(3)、若a=30,b=10,每米护栏造价80元,求建此停车场所需的费用.23. 【教材呈现】如图是华师版七年级上册数学教材第176页的部分内容.有了“两直线平行,同位角相等”,我们就能用推理的方法得出“两条平行线被第三条直线所截,内错角相等”.
如图①,已知平行线a、b被直线l所截,我们将∠1的对顶角记为∠3.
(1)、下面是“两直线平行,内错角相等”的推理过程,在括号内填写理由.∵a∥b( ),
∴∠2=∠3( ).
∵∠1=∠3( ),
∴∠1=∠2( ).
(2)、【拓展应用】如图②,AB∥CD,BC∥DE,若∠B=47°,则∠D=°.(3)、如图③,已知AB∥CD,∠1=∠2,试说明∠BEF=∠EFC.24. 如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方. (1)、图1中∠AOC=度.(2)、将图1中的三角板绕点O逆时针旋转至图2所示位置,使一边OM在∠BOC内部,且恰好平分∠BOC,若点D、O、N三点共线,则∠AOD=度.(3)、将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 . (直接写出结果)(4)、将图1中的三角板绕点O顺时针旋转,请探究,当ON始终在∠AOC的内部时(如图3),∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.
(1)、图1中∠AOC=度.(2)、将图1中的三角板绕点O逆时针旋转至图2所示位置,使一边OM在∠BOC内部,且恰好平分∠BOC,若点D、O、N三点共线,则∠AOD=度.(3)、将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 . (直接写出结果)(4)、将图1中的三角板绕点O顺时针旋转,请探究,当ON始终在∠AOC的内部时(如图3),∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请举例说明.