2014年全国高考理数真题试卷(新课标I卷)
试卷更新日期:2016-09-28 类型:高考真卷
一、选择题
-
1. 已知集合A={x|x2﹣2x﹣3≥0},B={x|﹣2≤x<2},则A∩B=( )A、[1,2) B、[﹣1,1] C、[﹣1,2) D、[﹣2,﹣1]2. =( )A、1+i B、1﹣i C、﹣1+i D、﹣1﹣i3. 设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论正确的是( )A、f(x)•g(x)是偶函数 B、|f(x)|•g(x)是奇函数 C、f(x)•|g(x)|是奇函数 D、|f(x)•g(x)|是奇函数4. 已知F为双曲线C:x2﹣my2=3m(m>0)的一个焦点,则点F到C的一条渐近线的距离为( )A、 B、3 C、m D、3m5. 4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为( )A、 B、 C、 D、6. 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P做直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]的图象大致为( )
 A、
A、 B、
B、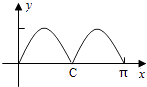 C、
C、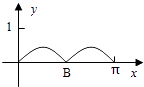 D、
D、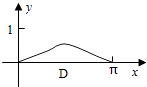 7.
7.执行如图的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=( )
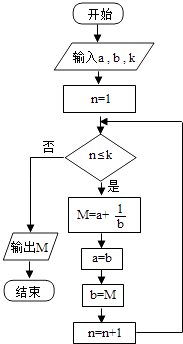 A、 B、 C、 D、8. 设α∈(0, ),β∈(0, ),且tanα= ,则( )A、3α﹣β= B、3α+β= C、2α﹣β= D、2α+β=9. 不等式组 的解集记为D,有下列四个命题:
A、 B、 C、 D、8. 设α∈(0, ),β∈(0, ),且tanα= ,则( )A、3α﹣β= B、3α+β= C、2α﹣β= D、2α+β=9. 不等式组 的解集记为D,有下列四个命题:p1:∀(x,y)∈D,x+2y≥﹣2 p2:∃(x,y)∈D,x+2y≥2
p3:∀(x,y)∈D,x+2y≤3 p4:∃(x,y)∈D,x+2y≤﹣1
其中真命题是( )
A、p2 , p3 B、p1 , p4 C、p1 , p2 D、p1 , p310. 已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若 =4 ,则|QF|=( )A、 B、3 C、 D、211. 已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0 , 且x0>0,则实数a的取值范围是( )A、(1,+∞) B、(2,+∞) C、(﹣∞,﹣1) D、(﹣∞,﹣2)12. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )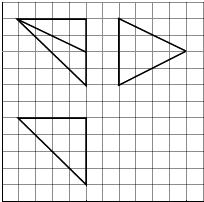 A、6 B、6 C、4 D、4
A、6 B、6 C、4 D、4二、填空题
-
13. (x﹣y)(x+y)8的展开式中x2y7的系数为 . (用数字填写答案)14. 甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一城市;
由此可判断乙去过的城市为 .
15. 已知A,B,C为圆O上的三点,若 = ( + ),则 与 的夹角为 .16. 已知a,b,c分别为△ABC的三个内角A,B,C的对边,a=2且(2+b)(sinA﹣sinB)=(c﹣b)sinC,则△ABC面积的最大值为 .三、解答题
-
17. 已知数列{an}的前n项和为Sn , a1=1,an≠0,anan+1=λSn﹣1,其中λ为常数.(1)、证明:an+2﹣an=λ(2)、是否存在λ,使得{an}为等差数列?并说明理由.18.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
 (1)、求这500件产品质量指标值的样本平均数 和样本方差s2(同一组中数据用该组区间的中点值作代表);(2)、由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数 ,σ2近似为样本方差s2 .
(1)、求这500件产品质量指标值的样本平均数 和样本方差s2(同一组中数据用该组区间的中点值作代表);(2)、由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数 ,σ2近似为样本方差s2 .(i)利用该正态分布,求P(187.8<Z<212.2);
(ii)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数,利用(i)的结果,求EX.
附: ≈12.2.
若Z~N(μ,σ2)则P(μ﹣σ<Z<μ+σ)=0.6826,P(μ﹣2σ<Z<μ+2σ)=0.9544.
19. 如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.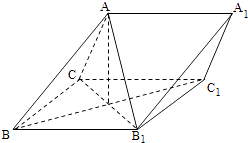 (1)、证明:AC=AB1;(2)、若AC⊥AB1 , ∠CBB1=60°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.20. 已知点A(0,﹣2),椭圆E: + =1(a>b>0)的离心率为 ,F是椭圆的焦点,直线AF的斜率为 ,O为坐标原点.(1)、求E的方程;(2)、设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.21. 设函数f(x)=aexlnx+ ,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.(1)、求a、b;(2)、证明:f(x)>1.
(1)、证明:AC=AB1;(2)、若AC⊥AB1 , ∠CBB1=60°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.20. 已知点A(0,﹣2),椭圆E: + =1(a>b>0)的离心率为 ,F是椭圆的焦点,直线AF的斜率为 ,O为坐标原点.(1)、求E的方程;(2)、设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.21. 设函数f(x)=aexlnx+ ,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.(1)、求a、b;(2)、证明:f(x)>1.四、选做题(22-24题任选一题作答,如果多做,则按所做的第一题计分) 选修4-1:几何证明选讲
