广东省普宁市2023-2024学年七年级上学期数学期末试卷

试卷更新日期：2024-03-05 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分．在每小题的四个选项中，只有一项正确）

1. 下列四个数中，最小的一个数是（）

A、-6 B、10 C、0 D、-1

查看试题解析
2. 如图是某个几何体的展开图，该几何体是（）

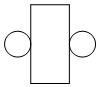A、圆锥 B、圆柱 C、圆台 D、四棱柱

查看试题解析
3. 2023年9月23日晚，以“潮起亚细亚”为主题的杭州亚运会盛大开幕，本次亚运会观众预计达到570万人次（）

A、 $5.7 \times 1 0^{2}$ B、 $5.7 \times 1 0^{4}$ C、 $5.7 \times 1 0^{5}$ D、 $5.7 \times 1 0^{6}$

查看试题解析
4. 如图所示数轴的单位长度为1，如果点A表示的数是-2，那么点B表示的数是（）

A、0 B、1 C、2 D、3

查看试题解析
5. 已知 $5 x^{m - 1} y^{2}$ 与 $\frac{1}{3} x^{5} y^{2}$ 是同类项，则m的值是（）

A、6 B、7 C、3 D、4

查看试题解析
6.
如图，C、D是线段AB上的两点，且D是线段AC的中点．若AB=10cm，BC=4cm，则AD的长为（　　）

A、2cm B、3cm C、4cm D、6cm

查看试题解析
7. 下列调查中，适宜采用抽样调查方式的是（）

A、调查奥运会上女子铅球参赛运动员兴奋剂的使用情况 B、调查某校某班学生的体育锻炼情况 C、调查一批灯泡的使用寿命 D、调查游乐园中一辆过山车上共40个座位的稳固情况

查看试题解析
8.
如图，下列表示角的方法，错误的是（　　）

A、∠1与∠AOB表示同一个角 B、∠AOC也可用∠O来表示 C、图中共有三个角：∠AOB、∠AOC、∠BOC D、∠β表示的是∠BOC

查看试题解析
9. 已知一个长方形的周长为30cm，若长方形的长减少1cm，宽扩大为原来的2倍后成为一个正方形，设原来长方形的长为xcm，则可列方程（）

A、x﹣1=2（15﹣x） B、x﹣1=2（30﹣x） C、 $x - 1 = \frac{1}{2} (15 - x)$ D、 $x - 1 = \frac{1}{2} (30 - x)$

查看试题解析
10. 如图，由等圆组成的一组图中，第①个图由1个圆组成，第②个图由5个圆组成，第③个图由11个圆组成，…，按照这样的规律排列下去，则第⑧个图由（）个圆组成

A、71 B、72 C、73 D、74

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分）

11. $- 2023$ 的绝对值是．

查看试题解析
12. 已知x=5是方程 $a x - 8 = 20 + a$ 的解，则 $a$ = ．

查看试题解析
13. 如图是一个正方体的平面展开图，若将展开图折叠成正方体后，相对面上所标的两个数互为相反数，则a的值为．

查看试题解析
14. 一副三角板按如图方式摆放，且 $∠ 1$ 的度数比 $∠ 2$ 的度数小 $30 °$ ，则 $∠ 1$ 的度数为 $°$ .

查看试题解析
15. 《义务教育课程标准（2022年版）》首次把学生学会炒菜纳入劳动教育课程，并做出明确规定．某班有50名学生，其中已经学会炒菜的学生频数是15，则该班学会炒菜的学生所占百分比是．

查看试题解析
16. 有理数a，b，c表示的点在数轴上的位置如图，化简 $|a + c| - |c - b| =$ ．

查看试题解析

三、解答题（本大题共9小题，满分72分．解答应写出文字说明、证明过程或演算步骤）

17. 计算： $- 1^{2023} + (- 8) + (- 4) - | - 5 |$

查看试题解析
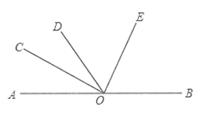
18. 解方程： $2 x + \frac{x - 1}{2} = - 3$ ．

查看试题解析
19. 先化简，再求值： $a^{2} - (3 a^{2} - 2 b^{2}) + (a^{2} - b^{2})$ ，其中 $a = - 3 ， b = 2$ ．

查看试题解析
20. 如图所示，AB为一条直线，OC是∠AOD的平分线，OE在∠BOD内，∠AOC=30° ，∠BOE=2∠DOE，求∠BOE的度数。

查看试题解析
21. 如图是由一些大小相同的小正方体组合成的简单几何体．

(1)、图中有几块小正方体；

(2)、该几何体从正面看到的形状图已画出，请在方格纸中分别画出从左面和从上面看到的该几何体的形状图．

查看试题解析
22. 随着科技的进步和网络资源的丰富，在线学习已成为更多人的自主学习选择．某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论．为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查（不可多选，也不可不选），并根据调查结果绘制成如下两幅不完整的统计图，根据图中信息，解答下列问题：

(1)、直接写出本次调查的总人数是：；

(2)、求出选择“在线听课”的人数，补全条形统计图；

(3)、求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

(4)、该校共有学生3000人，请你估计该校对在线阅读最感兴趣的学生有多少人？

查看试题解析
23. 定义一种新的运算，观察下列各式：
$1 ⊙ 2 = 1 + 2 \times 3 = 7$ ， $4 ⊙ (- 1) = 4 + (- 1) \times 3 = 1$ ， $(- 3) ⊙ 2 = - 3 + 2 \times 3 = 3$ ， $(- 6) ⊙ (- 4) = - 6 + (- 4) \times 3 = - 18$ ．

(1)、根据你观察到的规律，计算 $8 ⊙ (- 2)$ ；

(2)、请你用代数式表示 $m ⊙ n$ 的结果；

(3)、若 $(m - n) ⊙ n = 2$ ，请计算 $(m - 4 n) ⊙ (2 n - 1)$ 的值．

查看试题解析
24. 春节即将来临，甲、乙两公司准备组织退休职工到某风景区游玩．甲、乙两公司共102人，其中甲公司的退休职工人数在51-100人之间，乙公司的退休职工人数在1-50人之间．经了解，该风景区的门票价格如下表：
数量（张）
1-50
51-100
101张及以上
单价（元/张）
60元
50元
40元
如果两公司分别单独购买门票，一共应付5500元．

(1)、如果甲、乙两公司联合起来购买门票，那么比各自购买门票共可以节省多少钱？

(2)、甲、乙两公司各有多少名退休职工准备参加游玩？

(3)、如果甲公司有12名退休职工因身体原因不能外出游玩，小明由此设计了下面三种购票方案：①两公司分别单独购买门票；②两公司联合购买90张门票；③两公司联合购买101张门票，请你通过计算，选出最省钱的购票方案．

查看试题解析
25. 如图，射线 $O M$ 上有A ， B ， C三点，满足 $O A = 40 c m ， A B = 30 c m ， B C = 20 c m$ ．点P从点O出发，沿 $O M$ 方向以 $2 c m / s$ 的速度匀速运动，点Q从点C出发在线段 $C O$ 上向点O匀速运动，两点同时出发，当点Q运动到点O时，点P ， Q停止运动．

(1)、若Q的速度为 $3 c m / s$ ，求 $P Q$ 两点相遇时， $O P$ 的长；

(2)、当点P与点Q都同时运动到线段 $A B$ 的中点时，求点Q的运动速度；

(3)、当 $P A = 2 P B$ 时，点Q运动到的位置恰好是线段 $O B$ 的中点，求点Q的运动速度．

查看试题解析

数量（张）	1-50	51-100	101张及以上
单价（元/张）	60元	50元	40元