广东省惠州市惠阳重点中学2023-2024学年八年级上学期期中数学试卷

试卷更新日期：2024-03-05 类型：期中考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 如图是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在△ABC中，若∠A＝40°，∠B＝100°，则∠C＝（　　）

A、70° B、60° C、50° D、40°

查看试题解析
3. 下列长度的三条线段能组成三角形的是（）

A、2，3，5 B、1，2，3 C、2，3，4 D、2，2，5

查看试题解析
4. 点 $A (2 ， - 1)$ 关于 $y$ 轴对称的点 $B$ 的坐标为（）

A、 $(2，1)$ B、 $(- 2，1)$ C、 $(2 ， - 1)$ D、 $(- 2 ， - 1)$

查看试题解析
5. 下列运算正确的是（）.

A、 $x \cdot x^{2} = x^{2}$ B、 ${(xy)}^{2} = {xy}^{2}$ C、 ${(x^{2})}^{3} = x^{6}$ D、 $x^{2} + x^{2} = x^{4}$

查看试题解析
6. 如图，工人师傅砌门时，常用木条EF固定门框ABCD，使其不变形，这种做法的根据是（）

A、两点之间线段最短 B、三角形两边之和大于第三边 C、长方形的四个角都是直角 D、三角形的稳定性

查看试题解析
7.
将一副直角三角板，按如图所示叠放在一起，则图中∠α的度数是( )

A、45° B、60° C、75° D、90°

查看试题解析
8. 等腰三角形的一个角为50°，则这个等腰三角形的底角为（）

A、65° B、65°或80° C、50°或65° D、40°

查看试题解析
9. 如图，在 $△ A B C$ 中，已知 $∠ B$ 和 $∠ C$ 的平分线相交于点 $D$ ，过点 $D$ 作 $E F / / B C$ 交 $A B$ 、 $A C$ 于点 $E$ 、 $F$ ，若 $△ A E F$ 的周长为 $10$ ， $B C = 6$ ，则 $△ A B C$ 的周长为（）

A、 $16$ B、 $17$ C、 $18$ D、 $15$

查看试题解析
10. 已知如图，等腰 $△ A B C$ ， $A B = A C$ ， $∠ B A C = 120 °$ ， $A D ⊥ B C$ 于点 $D$ ，点 $P$ 是 $B A$ 延长线上一点，点 $O$ 是线段 $A D$ 上一点， $O P = O C$ ，下面的结论： $① ∠ A P O + ∠ D C O = 30 °$ ； $② ∠ A P O = ∠ D C O$ ； $③ △ O P C$ 是等边三角形； $④ A B = A O + A P .$ 其中正确的是（）

A、 $① ③ ④$ B、 $① ② ③$ C、 $① ③$ D、 $① ② ③ ④$

查看试题解析

二、填空题：本题共6小题，每小题4分，共24分。

11. 一个多边形的内角和是720°，这个多边形的边数是．

查看试题解析
12. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 60 °$ ， $B C = 2 c m$ ，则 $A B$ 的长是 $c m$ ．

查看试题解析
13. 计算： $x^{3} \cdot x^{5} =$ .

查看试题解析
14. 如图， $△ A B C$ 中， $A B = A C$ ， $A B$ 的垂直平分线交 $A C$ 于 $E$ ，连接 $B E$ ， $A B + B C = 16 c m$ ，则 $△ B C E$ 的周长是 $c m$ ．

查看试题解析
15. 如图， $O P$ 平分 $∠ A O B$ ， $∠ A O P = 15 °$ ， $P C / / O A$ ， $P D ⊥ O A$ 于点 $D$ ， $P C = 4$ ，则 $P D =$ ．

查看试题解析
16. 如图，△ABC的面积为12，AB＝AC，BC＝4，AC的垂直平分线EF分别交AB，AC边于点E，F，若点D为BC边的中点，点P为线段EF上一动点，则△PCD周长的最小值为．

查看试题解析

三、解答题：本题共9小题，共66分。解答应写出文字说明，证明过程或演算步骤。

17.

(1)、 $(π - 2023)^{0} - | 1 - 2 | + (- 2)^{3}$ ；

(2)、 $(x^{3} y + 2 x^{2} y^{2}) \div x y$ ．

查看试题解析
18. 如图，点 $B$ ， $E$ ， $C$ ， $F$ 在一条直线上， $A B = D E$ ， $A B / / D E$ ， $B E = C F$ ，求证： $∠ A = ∠ D$ ．

查看试题解析
19. 先化简，再求值： $(x + y) (x - 2 y) - x (x + y) + 2 x y$ ，其中 $x = (3 - π)^{0}$ ， $y = 2$ ．

查看试题解析
20. 如图，在平面直角坐标系中， $△ A B C$ 的顶点都在网格格点上，点 $A$ 、 $B$ 、 $C$ 的坐标分别为 $(1，2)$ 、 $(3，1)$ 、 $(4，4)$ ．

(1)、作出 $△ A B C$ 关于 $y$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ， $△ A_{1} B_{1} C_{1}$ 各顶点坐标为 $A_{1} ($ ▲ ， ▲ $)$ 、 $B_{1} ($ ▲ ， ▲ $)$ 、 $C_{1} ($ ▲ ， ▲ $)$ ；

(2)、 $△ A_{1} B_{1} C_{1}$ 的面积为；

(3)、在 $x$ 轴上作出一点 $P$ ，使得 $P A + P C$ 最短，点 $P$ 的坐标为 $($ ▲ ， ▲ $) .$

查看试题解析
21. 如图，在 $△ A B C$ 和 $△ D B C$ 中， $∠ A C B = ∠ D B C = 90 °$ ，点 $E$ 是 $B C$ 的中点， $D E ⊥ A B$ 于点 $F$ ，且 $A B = D E$ ．

(1)、求证： $△ A C B$ ≌ $△ E B D$ ；

(2)、若 $D B = 12$ ．
$①$ 求 $A C$ 的长；
$②$ 求 $△ D C E$ 的面积．

查看试题解析
22. 如图， $A$ ， $B$ ， $D$ 在同一条直线上， $∠ A = ∠ D = 90 °$ ， $A B = D E$ ， $∠ B C E = ∠ B E C$ ．

(1)、求证： $△ A C B$ ≌ $△ D B E$ ；

(2)、求证： $C B ⊥ B E$ ．

查看试题解析
23. 如图， $△ D A C$ 和 $△ E B C$ 均是等边三角形，点 $A$ 、 $B$ 、 $C$ 在同一直线上， $A E$ 与 $B D$ 交于点 $O$ ， $A E$ 、 $B D$ 分别与 $C D$ 、 $C E$ 交于点 $M$ 、 $N$ ．

(1)、求证： $△ A C E$ ≌ $△ D C B$ ；

(2)、求证： $∠ A O D = 60 °$ ；

(3)、求证： $△ C M N$ 是等边三角形．

查看试题解析
24. 如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．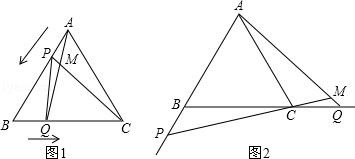

(1)、求证：△ABQ≌△CAP；

(2)、当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．

(3)、如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．

查看试题解析
25. 如图1，在平面直角坐标系中，△AOB为等腰直角三角形，A（4，4）

(1)、求B点坐标；

(2)、如图2，若C为x轴正半轴上一动点，以AC为直角边作等腰直角△ACD，∠ACD=90°连OD，求∠AOD的度数；

(3)、如图3，过点A作y轴的垂线交y轴于E，F为x轴负半轴上一点，G在EF的延长线上，以EG为直角边作等腰Rt△EGH，过A作x轴垂线交EH于点M，连FM，等式AM=FM+OF是否成立？若成立，请证明：若不成立，说明理由．

查看试题解析