广东省中山市2023-2024学年七年级上学期数学期末试卷
试卷更新日期:2024-03-05 类型:期末考试
一、单项选择题(共10个小题,每小题3分,满分30分)
-
1. 的倒数是( )A、 B、 C、 D、2. 2023年10月26日11时14分,搭载神舟十七号载人飞船的长征二号F遥十七运载火箭在酒泉卫星发射中心点火发射.若火箭发射点火前5秒记为秒,那么火箭发射点火后10秒应记为( )A、秒 B、秒 C、秒 D、秒3. 下列式子是单项式的是( )A、 B、 C、 D、4. 地球与太阳之间的距离约为149600000千米,将149600000用科学记数法表示应为( ).A、 B、 C、 D、5. 如图,已知点O在直线 AB上, ,则 的余角是( )
 A、 B、 C、 D、6. 根据等式的性质,如果 , 则下列结论正确的是( )A、 B、 C、 D、7. 植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,这其中用到的数学道理是( )A、两点之间,线段最短 B、两点确定一条直线 C、线段只有一个中点 D、两条直线相交,只有一个交点8. 下列各算式的结果中,值最小的是( )A、 B、 C、 D、9. 按照如图所示的计算程序,若x=2,则输出的结果是( )
A、 B、 C、 D、6. 根据等式的性质,如果 , 则下列结论正确的是( )A、 B、 C、 D、7. 植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,这其中用到的数学道理是( )A、两点之间,线段最短 B、两点确定一条直线 C、线段只有一个中点 D、两条直线相交,只有一个交点8. 下列各算式的结果中,值最小的是( )A、 B、 C、 D、9. 按照如图所示的计算程序,若x=2,则输出的结果是( ) A、16 B、26 C、﹣16 D、﹣2610. 在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
A、16 B、26 C、﹣16 D、﹣2610. 在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是
 A、甲>乙>丙 B、甲>丙>乙 C、丙>甲>乙 D、丙>乙>甲
A、甲>乙>丙 B、甲>丙>乙 C、丙>甲>乙 D、丙>乙>甲二、填空题(共5个小题,每小题4分,满分20分)
-
11. 的相反数是 .12. 若是关于x的方程的解,则m的值为 .13. 如图,点C , D在线段上,其中 , 若 , 则 .
 14. 如果实际值为a , 测量值为b , 我们把称为绝对误差,称为相对误差.若有种零件实际长度为 , 测量得 , 则测量所产生的相对误差是 .15. 已知 , 当x分别取1、2、3、…、2024时,所对应T值的总和是 .
14. 如果实际值为a , 测量值为b , 我们把称为绝对误差,称为相对误差.若有种零件实际长度为 , 测量得 , 则测量所产生的相对误差是 .15. 已知 , 当x分别取1、2、3、…、2024时,所对应T值的总和是 .三、解答题(一)(共4个小题,每小题6分,满分24分)
-
16. 计算: .17. 解方程:18. 化简: .19. 如图,已知直线l和直线外三点A , B , C , 请按下列要求画图(不写作法,但C、要保留作图痕迹):
 (1)、画射线;(2)、连接;(3)、在直线l上确定点D , 使得的和最小.
(1)、画射线;(2)、连接;(3)、在直线l上确定点D , 使得的和最小.四、解答题(二)(共3个小题,每小题8分,满分24分)
-
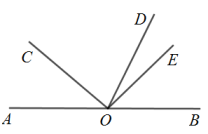
20. 如图,点是直线上一点,平分 , , 若 , 求的度数.
 21. 第19届亚运会于2023年9月23日至10月8日在杭州举行.中国运动员发扬顽强拼搏的精神,在比赛场上屡创佳绩.本次亚运会中国队获得金、银、铜牌共383枚,其中金牌比银牌的2倍少21枚,铜牌比银牌少40枚.问金、银、铜牌各是多少枚?(请列方程解答)22. 一般情况下,算式不成立,但有些特殊的a , b可以使得它成立,例如:等.我们称使得成立的一对数a , b为“相伴数对”,记为 .(1)、若是“相伴数对”,求b的值;(2)、若是“相伴数对”,求代数式的值.
21. 第19届亚运会于2023年9月23日至10月8日在杭州举行.中国运动员发扬顽强拼搏的精神,在比赛场上屡创佳绩.本次亚运会中国队获得金、银、铜牌共383枚,其中金牌比银牌的2倍少21枚,铜牌比银牌少40枚.问金、银、铜牌各是多少枚?(请列方程解答)22. 一般情况下,算式不成立,但有些特殊的a , b可以使得它成立,例如:等.我们称使得成立的一对数a , b为“相伴数对”,记为 .(1)、若是“相伴数对”,求b的值;(2)、若是“相伴数对”,求代数式的值.五、解答题(三)(共2个小题,第23题10分,第24题12分,满分22分)
-
23. 如图是由正奇数排成的数阵:
 (1)、请计算图中“工”形框中七个数的和是中间数45的几倍;(2)、在数阵中任意做一个这样的“工”形框,(1)中的关系是否仍成立?并写出理由;(3)、用这样的“工”形框能框出和为2023的七个数吗?如果能,求出这七个数中间的数;如果不能,请写出理由.24. 对于数轴上的三点A , B , C , 给出如下定义:若 , 则称点C叫做点A , B的“距离和m点”.如图,点A表示的数为 , 点B表示的数为2,点C表示的数为0.由于 , 则点C为点A , B的“距离和5点”;由于 , 则点A为点B , C的“距离和8点”.
(1)、请计算图中“工”形框中七个数的和是中间数45的几倍;(2)、在数阵中任意做一个这样的“工”形框,(1)中的关系是否仍成立?并写出理由;(3)、用这样的“工”形框能框出和为2023的七个数吗?如果能,求出这七个数中间的数;如果不能,请写出理由.24. 对于数轴上的三点A , B , C , 给出如下定义:若 , 则称点C叫做点A , B的“距离和m点”.如图,点A表示的数为 , 点B表示的数为2,点C表示的数为0.由于 , 则点C为点A , B的“距离和5点”;由于 , 则点A为点B , C的“距离和8点”. (1)、若点N表示的数为 , 点N为点A , B的“距离和m点”,求m的值;(2)、点D在数轴上,若点D是点A , B的“距离和7点”,求点D表示的数;(3)、点E在数轴上,若点E , A , B中的一点是另两点的“距离和6点”,求点E所表示的数.
(1)、若点N表示的数为 , 点N为点A , B的“距离和m点”,求m的值;(2)、点D在数轴上,若点D是点A , B的“距离和7点”,求点D表示的数;(3)、点E在数轴上,若点E , A , B中的一点是另两点的“距离和6点”,求点E所表示的数.