浙江省金华市永康三中2023-2024学年九年级（上）第二次独立作业数学试卷

试卷更新日期：2024-03-05 类型：月考试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 永康市2024年1月1日是晴天，这个事件是（）

A、必然事件 B、确定性事件 C、随机事件 D、不可能事件

查看试题解析
2. 下列函数是二次函数的是（）

A、 $y = \frac{2}{x^{2} + 1}$ B、 $y = 2 x$ C、 $y = \sqrt{x^{2} + 4}$ D、 $y = - 3 x^{2}$

查看试题解析
3. 如图，一名滑雪运动员沿着倾斜角为 $α$ 的斜坡，从 $A$ 滑行到 $B$ . 已知 $A B = 200 m$ ，
则这名滑雪运动员的高度下降了（）m

A、 $200 s i n α$ B、 $200 c o s α$ C、 $200 t a n α$ D、 $\frac{200}{t a n α}$

查看试题解析
4. 抛物线 $y = 2 {（x + 2）}^{2} - 5$ 可由 $y = 2 x^{2}$ 如何平移得到（）

A、先向右平移2个单位，再向下平移5个单位 B、先向右平移2个单位，再向上平移5个单位 C、先向左平移2个单位，再向下平移5个单位 D、先向左平移2个单位，再向上平移5个单位

查看试题解析
5. 二次函数 $y = - 5 {(x + 2)}^{2} - 6$ 的开口方向、对称轴和顶点坐标分别为（）

A、向下、直线x=2、（2，6） B、向下、直线、（-2，-6） C、向下、直线、（-2，6） D、向上、直线、（2，-6）

查看试题解析
6. 有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③平分弦的直径垂直弦；④相等的圆周角所对的弧相等．其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 如图， $⊙$ O的半径为5，直角三角板30°角的顶点A落在 $⊙$ O上，两边与 $⊙$ O交于点B，C，则弦BC的长为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 已知点P是线段AB的黄金分割点，AP $>$ PB，若AB=4，则PB=（）

A、 $2 \sqrt{5} - 2$ B、 $2 \sqrt{5} + 2$ C、 $6 - 2 \sqrt{5}$ D、 $2 \sqrt{5} - 4$

查看试题解析
9. 在解决代数问题时我们常会通过构建几何图形来分析.比如在计算tan15°时，如图，在Rt△ACB中，∠C＝90°，∠ABC＝30°，延长CB使BD＝AB，连接AD，得∠D＝15°，所以tan15° $= \frac{A C}{C D} = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ．类比这种方法，可得tan22.5°的值为（）

A、 $\sqrt{2} + 1$ B、 $\sqrt{2} - 1$ . C、 $\sqrt{2}$ D、 $\frac{1}{2}$

查看试题解析
10. 如图，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，以此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S₁ ， S₂ ， S₃ ， …，S₁₀ ，则S₁+S₂+S₃+…+S₁₀=（）

A、4π B、3π C、2π D、π

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

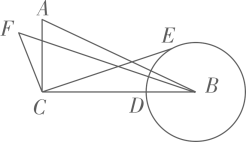
11. 已知线段a＝1，b＝4，则线段a、b的比例中项为．

查看试题解析
12. 已知圆的半径为2cm，90°圆心角所对的弧长为cm.

查看试题解析
13. 已知圆锥的母线长为20cm，底面半径为4cm，则这个圆锥的侧面积为 ${c m}^{2}$ ．

查看试题解析
14. 两个相似三角形的面积比为4：9，其中较小三角形的周长为4，则较大三角形的周长为．

查看试题解析
15. 已知函数y＝mx²+3mx+m﹣1的图象与坐标轴恰有两个公共点，则实数m的值为．

查看试题解析
16. 如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝6，BD＝2，以点B为圆心，BD长为半径作圆，点E为 $⊙ B$ 上的动点，连结EC，作FC⊥CE，垂足为C，点F在直线BC的上方，且满足 $C F = \frac{1}{2} C E$ ，连结BF.当点E与点D重合时，BF的值为.点E在 $⊙ B$ 上运动过程中，BF存在最大值为.

查看试题解析

三、简答题（本题有8小题，共66分）

17. 计算：

(1)、 $2 t a n 6 0^{°} \times c o s 3 0^{°} - 4 s i n^{2} 6 0^{°}$ .

(2)、 $\frac{3 t a n 30 ° - 2 t a n 45 °}{c o s 60 °}$ .

查看试题解析
18. 某校开展了自主选课活动．小明和小王分别打算从以下四个特色课程中随机选一个参加：
A．竞技乒乓，B．围棋博弈，C．名著阅读，D．街舞少年．

(1)、小明选择街舞少年的概率为．

(2)、请用画树状图或列表的方法求小明和小王选择到同一个课程的概率.

查看试题解析
19. 已知：线段a，b，c，且 $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ .

(1)、求 $\frac{a + b}{b}$ 的值；

(2)、如果对于线段a，b，c，满足a+b+c=36，求a，b，c的值.

查看试题解析
20. 为了防洪需要，某地决定新建一座拦水坝.如图，拦水坝的横断面为梯形ABCD，斜面坡度i=3：4（即斜面的铅直高度AF与水平宽度BF的比）.已知斜坡CD的长度为20m，∠C=18°，求斜坡AB的长.（结果精确到0.1m，参考数据：sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）

查看试题解析
21. 如图，AB是⊙O的直径，点C是弧BE中点，AE⊥CD于点D，延长DC，AB交于点F，已知AD＝4，FC＝ $\sqrt{2}$ FB.

(1)、求证：CD与⊙O相切．

(2)、求⊙O的半径．

查看试题解析
22. 某大学生创业团队抓住商机，购进一批干果分装成营养搭配合理的小包装后出售，每袋成本3元．试销期间发现每天的销售量y（袋）与销售单价x（元）之间满足一次函数关系，另外每天还需支付其他各项费用100元．
销售单价x（元）
3.5
4
4.5
5
5.5
销售量y（袋）
350
300
250
200
150

(1)、求出y与x之间的函数关系式．

(2)、为了在春节前将这批干果销售完，每天的销量不能低于150袋，如果每天获得200元的利润，销售单价为多少元？

(3)、若每天的销量不能低于150袋，当销售单价定为多少元时，每天的利润最大？最大利润是多少元？

查看试题解析
23. 对于平面直角坐标系xOy中的图形P、Q，给出如下定义：点M为图形P上任意一点，点N为图形Q上任意一点，如果M，N两点间的距离有最小值，那么就称这个最小值为图形P，Q间的“非常距离”，记作d（P，Q）．已知点A（-2，2），B（2，2），连接AB．

(1)、d（点O，AB）＝；

(2)、⊙O半径为r，若d（⊙O，AB）=0，则r的取值范围是；

(3)、⊙O半径为r，若将点A绕点B逆时针旋转 $α^{°} (0^{°} < α < 18 0^{°})$ ，得到点 $A^{'}$ ．
①当 $α = 3 0^{∘}$ 时，d（⊙O， $A^{'}$ ）=0，求出此时r的值；
②对于取定的r值，若存在两个α使d（⊙O， $A^{'}$ ）=0，则 r的取值范围是 ▲ ．

查看试题解析
24. 如图1，已知抛物线F₁：y＝﹣x²+2x+3交x轴于A、B两点，与y轴交于点C，抛物F₂：y＝ $\frac{1}{2}$ x²+bx+c经过点A、B，点P是射线CB上一动点.

(1)、求抛物线F₂的表达式．

(2)、如图2，过点P作PE⊥BC交抛物线F₁第一象限部分于点E，作EF $∕ ∕$ AB交BC于点F，求△PEF面积的最大值及此时点E的坐标．

(3)、抛物线F₁与F₂在第一象限内的图象记为“图象Z ”，过点P作PG $∕ ∕$ y轴交图象Z于点G，是否存在这样的点P，使△CPG与△OBC相似？若存在，求出所有符合条件的点P的横坐标．

查看试题解析

销售单价x（元）	3.5	4	4.5	5	5.5
销售量y（袋）	350	300	250	200	150