广东省初中2023-2024学年中考模拟预测(一)数学试卷
试卷更新日期:2024-03-05 类型:中考模拟
一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 计算-3-2的结果等于( )A、1 B、-1 C、-5 D、52. 据国家电影局初步统计,2023年春节档(1月21日至1月27日)电影票房约为6758000000元,数据6758000000用科学记数法表示为( ).A、 B、 C、 D、3. 如图是由4个相同的正方体搭成的几何体,则其俯视图是( )
 A、
A、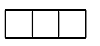 B、
B、 C、
C、 D、
D、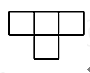 4. 计算(-2x2)3的结果是( )A、-8x6 B、-8x5 C、8x6 D、8x55. 如图,直线AB‖CD,若∠1=60°,则∠2为( )
4. 计算(-2x2)3的结果是( )A、-8x6 B、-8x5 C、8x6 D、8x55. 如图,直线AB‖CD,若∠1=60°,则∠2为( ) A、60° B、110° C、120° D、130°6. 一组数据-3,a,2,3,5有唯一的众数3,则这组数据的中位数是( )A、-2 B、1 C、3 D、57. 如图,BC是⊙O的直径,点A,D在⊙O上,若∠ADC=30°,则∠ACB的度数为( )
A、60° B、110° C、120° D、130°6. 一组数据-3,a,2,3,5有唯一的众数3,则这组数据的中位数是( )A、-2 B、1 C、3 D、57. 如图,BC是⊙O的直径,点A,D在⊙O上,若∠ADC=30°,则∠ACB的度数为( ) A、30° B、40° C、50° D、60°8. 关于x的一元二次方程x2-kx+2=0有实数根,则k可能是 ( )A、-3 B、-2 C、1 D、9. 古希腊数学家把数1,3,6,10,15,21,…,叫做三角形数,它有一定的规律性,若把第一个三角形数记为a1 , 第二个三角形数记为a2 , …,第n个三角形数记为an , 则an+an+1的值为( )A、(n+1)2 B、n2 C、n D、n+110. 如图,在平面直角坐标系中,直线y=-3x+3交x轴于点A,交y轴于点B,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线y=k/x上,现将正方形ABCD沿y轴向下平移a个单位长度,可以使得顶点C落在双曲线上,则a的值为( )
A、30° B、40° C、50° D、60°8. 关于x的一元二次方程x2-kx+2=0有实数根,则k可能是 ( )A、-3 B、-2 C、1 D、9. 古希腊数学家把数1,3,6,10,15,21,…,叫做三角形数,它有一定的规律性,若把第一个三角形数记为a1 , 第二个三角形数记为a2 , …,第n个三角形数记为an , 则an+an+1的值为( )A、(n+1)2 B、n2 C、n D、n+110. 如图,在平面直角坐标系中,直线y=-3x+3交x轴于点A,交y轴于点B,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线y=k/x上,现将正方形ABCD沿y轴向下平移a个单位长度,可以使得顶点C落在双曲线上,则a的值为( )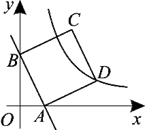 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 实数
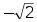 的相反数是. 12. 已知α是锐角,且cosα= , 那么α=.13. 若
的相反数是. 12. 已知α是锐角,且cosα= , 那么α=.13. 若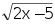 有意义,则x的取值范围是. 14. 按照如图所示的操作步骤,若输入x的值为-2,则输出的值为.
有意义,则x的取值范围是. 14. 按照如图所示的操作步骤,若输入x的值为-2,则输出的值为. 15. 如图,从一个边长是10的正五边形纸片上剪出一个扇形(阴影部分),将剪下来的扇形围成一个圆锥,则这个圆锥的底面半径为 .
15. 如图,从一个边长是10的正五边形纸片上剪出一个扇形(阴影部分),将剪下来的扇形围成一个圆锥,则这个圆锥的底面半径为 .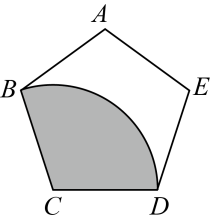
三、 解答题(一):本大题共3小题,每小题8分,共24分.
-
16. 计算:17. 先化简,再求值: , 其中 .18. 如图,在△ABC中,D是BC延长线上的一点,CD=AB,过点C作CE‖AB且CE=BC,连接DE并延长,分别交AC,AB于点F,G.
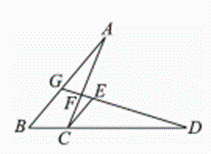 (1)、求证:△ABC≌△DCE;(2)、若∠B=50°,∠D=25°,求∠AFG的度数.
(1)、求证:△ABC≌△DCE;(2)、若∠B=50°,∠D=25°,求∠AFG的度数.四、 解答题(二):本大题共3小题,每小题9分,共27分.
-
19. 如图,在⊙O中,直径AB=10,弦AC=8,连接BC.
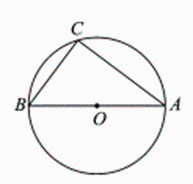 (1)、尺规作图:过点O作弦AC的垂线,交AC于点E,交⊙O于点D,且点D在劣弧AC之间;(2)、连接AD,求△OAD的面积.20. 某单位食堂为全体职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如图:
(1)、尺规作图:过点O作弦AC的垂线,交AC于点E,交⊙O于点D,且点D在劣弧AC之间;(2)、连接AD,求△OAD的面积.20. 某单位食堂为全体职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如图: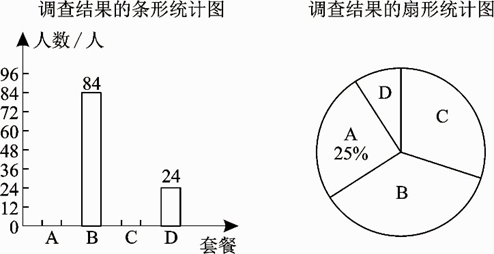 (1)、在抽取的240人中最喜欢A套餐的人数为人,扇形统计图中“C”对应扇形的圆心角的大小为;(2)、依据本次调查的结果,估计全体960名职工中最喜欢D套餐的人数;(3)、现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,请用画树状图法或列表法求甲、乙被选到的概率.21. 为庆祝两会的胜利召开,某中学举行了以“两会”为主题的知识竞赛,现决定购买同一品牌的钢笔和自动铅笔作为获奖学生的奖品,到文教店查看定价后发现,购买2支钢笔和5支自动铅笔共需75元,购买3支钢笔和2支自动铅笔共需85元.(1)、求该品牌的钢笔、自动铅笔每支的定价分别是多少元;(2)、经协商,文教店给予该校购买一支该品牌钢笔赠送一支自动铅笔的优惠,如果学校需要自动铅笔的支数是钢笔的支数的2倍还多8支,且学校购买钢笔和自动铅笔的总费用少于670元,那么学校最多可购买多少支该品牌的钢笔?
(1)、在抽取的240人中最喜欢A套餐的人数为人,扇形统计图中“C”对应扇形的圆心角的大小为;(2)、依据本次调查的结果,估计全体960名职工中最喜欢D套餐的人数;(3)、现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,请用画树状图法或列表法求甲、乙被选到的概率.21. 为庆祝两会的胜利召开,某中学举行了以“两会”为主题的知识竞赛,现决定购买同一品牌的钢笔和自动铅笔作为获奖学生的奖品,到文教店查看定价后发现,购买2支钢笔和5支自动铅笔共需75元,购买3支钢笔和2支自动铅笔共需85元.(1)、求该品牌的钢笔、自动铅笔每支的定价分别是多少元;(2)、经协商,文教店给予该校购买一支该品牌钢笔赠送一支自动铅笔的优惠,如果学校需要自动铅笔的支数是钢笔的支数的2倍还多8支,且学校购买钢笔和自动铅笔的总费用少于670元,那么学校最多可购买多少支该品牌的钢笔?五、 解答题(三):本大题共2小题,每小题12分,共24分.
-
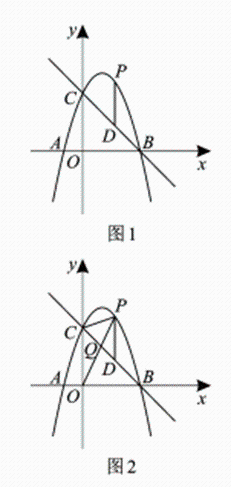
22. 如图1,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在左侧),与y轴交于点C,点P为直线BC上方抛物线上的一个动点,过点P作PD‖y轴交BC于点D.
 (1)、求点A、B、C的坐标;(2)、设点P的横坐标为m,请用含m的式子表示线段PD的长;(3)、如图2,连接OP,交线段BC于点Q,连接PC,若△PCQ的面积为S1 , △OCQ的面积为S2 , 则是否有最大值?如果有,请求出最大值;如果没有,请说明理由.23. 如图1,E为正方形ABCD内一动点,且∠AEB=90°,将BE绕点B按顺时针旋转90°,得到BE’,连接CE’,延长AE交CE’于点F,连接DE.
(1)、求点A、B、C的坐标;(2)、设点P的横坐标为m,请用含m的式子表示线段PD的长;(3)、如图2,连接OP,交线段BC于点Q,连接PC,若△PCQ的面积为S1 , △OCQ的面积为S2 , 则是否有最大值?如果有,请求出最大值;如果没有,请说明理由.23. 如图1,E为正方形ABCD内一动点,且∠AEB=90°,将BE绕点B按顺时针旋转90°,得到BE’,连接CE’,延长AE交CE’于点F,连接DE.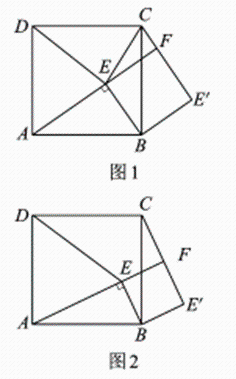 (1)、 求证:△ABE≌△CBE’;(2)、 如图1,若DA=DE,请猜想线段CE’与FE’的数量关系并加以证明;(3)、 如图2,若AB=15,CF=3,求DE的长.
(1)、 求证:△ABE≌△CBE’;(2)、 如图1,若DA=DE,请猜想线段CE’与FE’的数量关系并加以证明;(3)、 如图2,若AB=15,CF=3,求DE的长.