广东省清远市清城区2024年中考数学一模试卷

试卷更新日期：2024-03-05 类型：中考模拟

进入出卷网下载

一、选择题（本大题10小题，每小题3分，共30分．在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．）

1. 中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录，下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列二次根式一定成立的是（　　）

A、 $\sqrt{2 m}$ B、 $\sqrt{m^{2} - 1}$ C、 $\sqrt{m^{2} + 1}$ D、 $\sqrt{m + 1}$

查看试题解析
3. 将有理数682000000用科学记数法表示，其中正确的是（）

A、68.2×10⁸ B、6.82×10⁸ C、6.82×10⁷ D、6.82×10⁹

查看试题解析
4. 已知在一个凸多边形中，和一个内角相邻的外角与其余内角度数总和为600°，则这个多边形的边数是（）

A、5 B、6 C、7 D、5或6

查看试题解析
5. 欣欣快餐店备有6种价格不同的菜，每份价格（元）分别为1，2，3，4，5，6．若某人任选两种不同价格的菜各一份，两种菜的价格和超过6元的概率是（　　）

A、 $\frac{11}{15}$ B、 $\frac{3}{5}$ C、 $\frac{1}{2}$ D、 $\frac{2}{5}$

查看试题解析
6. 下列运算结果正确的是（　　）

A、2a+2a＝4a² B、（﹣a²b）³＝﹣a⁵b³ C、a²•a²＝a⁴ D、（a﹣2b）²＝a²﹣4b²

查看试题解析
7. 下列说法正确的是（　　）

A、一组数据2，2，3，4的众数是2，中位数是2.5 B、了解某市市民知晓“礼让行人”交通新规的情况，适合全面调查 C、甲、乙两人跳远成绩的方差分别为S²_甲＝3，S²_乙＝4，说明乙的跳远成绩比甲稳定 D、打开电视机，正在播放“襄阳新闻”是必然事件

查看试题解析
8. 在Rt△ABC中，∠C＝90°，∠BAC的角平分线AD交BC于点D ， BC＝7，BD＝4，则点D到AB的距离是（　　）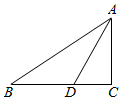

A、3 B、4 C、5 D、7

查看试题解析
9. 如图，菱形OABC的边OA在平面直角坐标系中的x轴上， $∠ A O C = 60 °$ ， $O A = 4$ ，则点C的坐标为（）

A、 $(2 ， 2 \sqrt{3})$ B、 $(2 \sqrt{3} ， 2)$ C、 $(2 \sqrt{3} ， 2 \sqrt{3})$ D、 $(2 ， 2)$

查看试题解析
10. 如图，抛物线y＝ax²+bx+c（a ， b ， c是常数，a≠0）与x轴交于A、B两点，顶点P（m ， n）．给出下列结论，正确的有（　　）
①abc＞0；
②9a﹣3b+c＜0；
③若点（ $- \frac{1}{2}$ ， y₁），（ $\frac{1}{2}$ ， y₂），（ $\frac{3}{2}$ ， y₃）在抛物线上，则y₂＜y₁＜y₃；
④关于x的ax²+bx+k＝0有实数解，则k≥c﹣n；
⑤当n＝ $- \frac{3}{a}$ 时，△ABP为等边三角形．

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题（共5小题，满分15分，每小题3分）

11. $2 t a n 45^{\circ} - (\sqrt{2} - π)^{0}$ ＝．

查看试题解析
12. 如图，AF是∠BAC的平分线，DF∥AC ，若∠1＝35°，则∠BAF的度数为．

查看试题解析
13. 不等式组 $\{\begin{array}{l} x - 2 < 0 \\ - 2 x - 1 ⩽ 1 \end{array}$ 的解集为．

查看试题解析
14. 有一个蓄水池，池内原有水60m³ ，现在向蓄水池注水，已知池内总水量y与注水时间x具有如下关系：
注水时间x（min）
0
1
2
3
…
池内水量y（m³）
60
72
84
96
…
在一定时间范围内，池内总水量y与注水时间x之间近似为一次函数关系，则该函数表达式为．

查看试题解析
15. 如图，AB是半圆O的直径，P是AB上的动点，CP⊥AB交半圆于点C ，已知AB＝2，则OP+PC的最大值是．

查看试题解析

三、解答题（共8小题，满分75分）

16. 先化简，后求值： $(\frac{1}{x - 2} + 1) \div \frac{x^{2} - 2 x + 1}{x^{2} - x}$ ，从﹣1，0，1，2选一个合适的值，代入求值．

查看试题解析
17. 对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污染，保护环境．为了了解同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取若干名同学进行了问卷测试．根据测试成绩分布情况，他们将全部测试成绩分成A、B、C、D四组，绘制了统计图表．
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
分数/分
频数
A
60＜x≤70
38
B
70＜x≤80
72
C
80＜x≤90
60
D
90＜x≤100
m

依据以上统计信息解答下列问题：

(1)、求得m＝， n＝；

(2)、为了增强大家对垃圾分类的了解，学校组织每个班级学习相关知识，经过一段时间的学习后，再次对原来抽取的这些同学进行问卷测试，发现A组的同学平均成绩提高15分，B组的同学平均成绩提高10分，C组的同学平均成绩提高5分，D组的同学平均成绩没有变化，请估计学习后这些同学的平均成绩提高多少分？若把测试成绩超过85分定为优秀，这些同学再次测试的平均成绩是否达到优秀，为什么？

查看试题解析
18. 如图，△ABC中，AB＝AC＞BC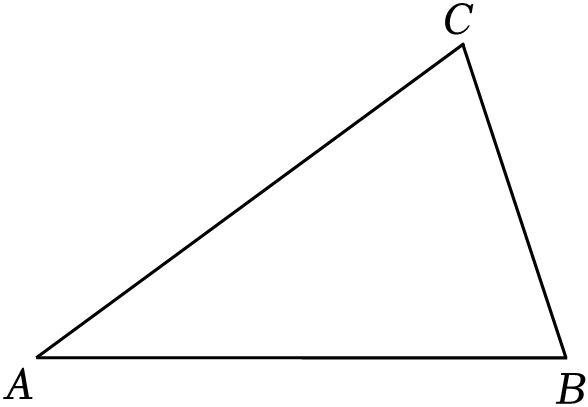

(1)、求作边AB的垂直平分线，交AC于点D；（要求：尺规作图，不写作法，保留作图痕迹）；

(2)、若BD＝BC ，求∠A的大小．

查看试题解析
19. 某地有甲、乙两家口罩厂，已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的2倍，并且乙厂单独完成24万只口罩的生产比甲厂单独完成24万只口罩的生产多用4天．

(1)、求甲、乙厂每天分别可以生产多少万只口罩？

(2)、该地委托甲、乙两厂尽快完成90万只口罩的生产任务，两厂同时生产至少需要多少天才能完成生产任务？

查看试题解析
20. 如图，在平面直角坐系xOy中，直线l：y＝kx+1（k≠0）与函数y＝ $\frac{m}{x}$ （x＞0）的图象G交于点A（1，2），与x轴交于点B ．

(1)、求k ， m的值；

(2)、点P为图象G上一点，过点P作x轴的平行线PQ交直线l于点Q ，作直线PA交x轴于点C ，若S_△_APQ：S_△_ACB＝1：4，求点P的坐标．

查看试题解析
21. 如图，在长方形ABCD中，AB＝3，BC＝4，点E是BC边上一点，连接AE ，将∠B沿直线AE折叠，使点B落在点B'处．

(1)、如图1，当点E与点C重合时，CB'与AD交于点F ，求证：FA＝FC；

(2)、如图2，当点E不与点C重合，且点B'在对角线AC上时，求CE的长．

查看试题解析
22. 如图，A ， B ， C是⊙O上的三点，且AB＝AC ， BC＝8，点D为优弧BDC上的动点，且cos∠ABC＝ $\frac{4}{5}$ ．

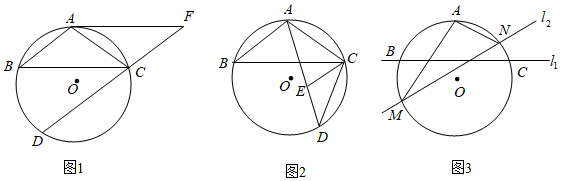(1)、如图1，若∠BCD＝∠ACB ，延长DC到F ，使得CF＝CA ，连接AF ，求证：AF是⊙O的切线；

(2)、如图2，若∠BCD的角平分线与AD相交于E ，求⊙O的半径与AE的长；

(3)、如图3，将△ABC的BC边所在的直线l₁绕点A旋转得到l₂ ，直线l₂与⊙O相交于M ， N ，连接AM ， AN ． l₂在运动的过程中，AM•AN的值是否发生变化？若不变，求出其值；若变化，说明变化规律．

查看试题解析
23. 抛物线y＝ax²+bx﹣2与x轴交于A、B两点（点A在点B的左侧），且A（﹣1，0），B（4，0），与y轴交于点C ．连结BC ，以BC为边，点O为中心作菱形BDEC ，点P是x轴上的一个动点，设点P的坐标为（m ， 0），过点P作x轴的垂线交抛物线于点Q ，交BD于点M ．

(1)、求该抛物线对应的函数表达式；

(2)、x轴上是否存在一点P ，使△PBC为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由；

(3)、当点P在线段OB上运动时，试探究：当m为何值时，四边形CQMD是平行四边形？请说明理由．

查看试题解析

注水时间x（min）	0	1	2	3	…
池内水量y（m³）	60	72	84	96	…

组别	分数/分	频数
A	60＜x≤70	38
B	70＜x≤80	72
C	80＜x≤90	60
D	90＜x≤100	m